Hostname: page-component-848d4c4894-jbqgn Total loading time: 0 Render date: 2024-06-17T06:14:22.688Z Has data issue: false hasContentIssue false
  • English
  • Français

Lattice Boltzmann simulations of low-Reynolds-number flows past fluidized spheres: effect of inhomogeneities on the drag force

Published online by Cambridge University Press:  07 November 2017

Gregory J. Rubinstein Open the ORCID record for Gregory J. Rubinstein [Opens in a new window] ,
Ali Ozel ,
Xiaolong Yin ,
J. J. Derksen  and
Sankaran Sundaresan
Gregory J. Rubinstein
Affiliation:
Department of Chemical and Biological Engineering, Princeton University, Princeton, NJ 08544, USA
Ali Ozel
Affiliation:
Department of Chemical and Biological Engineering, Princeton University, Princeton, NJ 08544, USA
Xiaolong Yin
Affiliation:
Department of Petroleum Engineering, Colorado School of Mines, Golden, CO 80401, USA
J. J. Derksen
Affiliation:
School of Engineering, University of Aberdeen, Aberdeen AB24 3UE, UK
Sankaran Sundaresan
Affiliation:
Department of Chemical and Biological Engineering, Princeton University, Princeton, NJ 08544, USA
Get access Rights & Permissions [Opens in a new window]

Abstract

The formation of inhomogeneities within fluidized beds, both in terms of the particle configurations and flow structures, have a pronounced effect on the interaction force between the fluid and particles. While recent numerical studies have begun to probe the effects of inhomogeneities on the drag force at the particle scale, the applicability of prior microscale constitutive drag relations is still limited to random, homogeneous distributions of particles. Since an accurate model for the drag force is needed to predict the fluidization behaviour, the current study utilizes the lessons of prior inhomogeneity studies in order to derive a robust drag relation that is both able to account for the effect of inhomogeneities and applicable as a constitutive closure to larger-scale fluidization simulations. Using fully resolved lattice Boltzmann simulations of systems composed of fluid and monodisperse spherical particles in the low-Reynolds-number (Re) regime, the fluid–particle drag force, normalized by the ideal Stokes drag force, is found to significantly decrease, over a range of length scales, as the extent of inhomogeneities increases. The extent of inhomogeneities is found to most effectively be quantified through one of two subgrid-scale quantities: the scalar variance of the particle volume fraction or the drift flux, which is the correlation between the particle volume fraction and slip velocity. Scale-similar models are developed to estimate these two subgrid measures over a wide range of system properties. Two new drag constitutive models are proposed that are not only functions of the particle volume fraction and the Stokes number (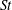$St$), but also dependent on one of these subgrid measures for the extent of inhomogeneities. Based on the observed, appreciable effect of inhomogeneities on drag, these new low-Re drag models represent a significant advancement over prior constitutive relations.

JFM classification

Multiphase and Particle-laden Flows: Fluidized beds Low-Reynolds-number flows: Low-Reynolds-number flows Multiphase and Particle-laden Flows: Multiphase and Particle-laden Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 833 , 25 December 2017 , pp. 599 - 630
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Agrawal, K., Loezos, P. N., Syamlal, M. & Sundaresan, S. 2001 The role of meso-scale structures in rapid gas–solid flows. J. Fluid Mech. 445, 151–185.Google Scholar
Beetstra, R., van der Hoef, M. A. & Kuipers, J. A. M. 2007 Drag force of intermediate Reynolds number flow past mono- and bidisperse arrays of spheres. AIChE J. 52 (2), 489–501.CrossRefGoogle Scholar
ten Cate, A., Nieuwstad, C. H., Derksen, J. J. & van den Akker, H. E. A. 2002 Particle imaging velocimetry experiments and lattice-Boltzmann simulations on a single sphere settling under gravity. Phys. Fluids 14 (11), 4012–4025.Google Scholar
Chen, S. & Doolen, G. D. 1998 Lattice Boltzmann method for fluid flows. Annu. Rev. Fluid Mech. 30, 329–364.Google Scholar
Cloete, S., Johansen, S. T. & Amini, S. 2015 Grid independence behaviour of fluidized bed reactor simulations using the Two Fluid Model: effect of particle size. Powder Technol. 269, 153–165.CrossRefGoogle Scholar
Derksen, J. & Van den Akker, H. E. A. 1999 Large-eddy simulations on the flow driven by a Rushton turbine. AIChE J. 45, 209–221.Google Scholar
Derksen, J. J. & Sundaresan, S. 2007 Direct numerical simulations of dense suspensions: wave instabilities in liquid-fluidized beds. J. Fluid Mech. 587, 303–336.Google Scholar
Eggels, J. G. M. & Somers, J. A. 1995 Numerical simulation of free convective flow using the lattice-Boltzmann scheme. Intl J. Heat Fluid Flow 16 (5), 357–364.Google Scholar
Fox, R. O. 2014 On multiphase turbulence models for collisional fluid–particle flows. J. Fluid Mech. 742, 368–424.Google Scholar
Fullmer, W. D. & Hrenya, C. M. 2016 Quantitative assessment of fine-grid kinetic-theory-based predictions of mean-slip in unbounded fluidization. AIChE J. 62 (1), 11–17.CrossRefGoogle Scholar
Garside, J. & Al-Dibouni, M. R. 1977 Velocity-voidage relationships for fluidization and sedimentation in solid–liquid systems. Ind. Eng. Chem. Process Des. Dev. 16, 206–214.CrossRefGoogle Scholar
Germano, M., Piomelli, U., Moin, P. & Cabot, W. H 1991 A dynamic subgrid-scale eddy viscosity model. Phys. Fluids A 3 (7), 1760–1765.Google Scholar
Goldstein, D., Handler, R. & Sirovich, L. 1993 Modeling a no-slip flow boundary with an external force field. J. Comput. Phys. 105 (2), 354–366.CrossRefGoogle Scholar
Hill, R. J., Koch, D. L. & Ladd, A. J. C. 2001 The first effects of fluid inertia on flows in ordered and random arrays of spheres. J. Fluid Mech. 448, 213–241.Google Scholar
van der Hoef, M. A., Beetstra, R. & Kuipers, J. A. M. 2005 Lattice-Boltzmann simulations of low-Reynolds-number flow past mono- and bidisperse arrays of spheres: results for the permeability and drag force. J. Fluid Mech. 528, 233–254.Google Scholar
Hong, K., Chen, S., Wang, W. & Li, J. 2016 Fine-grid two-fluid modeling of fluidization of Geldart A particles. Powder Technol. 296, 2–16.Google Scholar
Igci, Y., Andrews, A. T. IV, Sundaresan, S., Pannala, S. & O’Brien, T. 2008 Filtered two-fluid models for fluidized gas-particle suspensions. AIChE J. 54 (6), 1431–1448.Google Scholar
Igci, Y. & Sundaresan, S. 2011 Constitutive models for filtered two-fluid models of fluidized gas-particle flows. Ind. Engng Chem. Res. 50, 13190–13201.Google Scholar
Jiménez, C., Ducros, F., Cuenot, B. & Bédat, B. 2001 Subgrid scale variance and dissipation of a scalar field in large eddy simulations. Phys. Fluids 13 (6), 1748–1754.Google Scholar
Kim, S. & Karilla, S. J. 1991 Microhydrodynamics: Principles and Selected Applications. Butterworth-Heinemann.Google Scholar
Kriebitzsch, S. H. L., van der Hoef, M. A. & Kuipers, J. A. M. 2013 Drag force in discrete particle models – continuum scale or single particle scale? AIChE J. 59 (1), 316–324.Google Scholar
Ladd, A. J. C. 1994 Numerical simulations of particulate suspensions via a discretized Boltzmann equation. Part 1. Theoretical foundation. J. Fluid Mech. 271, 285–309.Google Scholar
Li, T., Gel, A., Pannala, S., Shahnam, M. & Syamlal, M. 2014 Reprint of ‘CFD simulations of circulating fluidized bed risers, part I: Grid study’. Powder Technol. 265, 2–12.CrossRefGoogle Scholar
Li, T., Wang, L., Rogers, W., Zhou, G. & Ge, W. 2017 An approach for drag correction based on the local heterogeneity for gas–solid flows. AIChE J 63 (4), 1203–1212.CrossRefGoogle Scholar
Liu, X., Zhu, C., Geng, S., Yao, M., Zhan, J. & Xu, G. 2015 Two-fluid modeling of Geldart A particles in gas–solid micro-fluidized beds. Particuology 21, 118–127.CrossRefGoogle Scholar
Lu, B., Wang, W. & Li, J. 2009 Searching for a mesh-independent sub-grid model for CFD simulation of gas–solid riser flows. Chem. Engng Sci. 64 (15), 3437–3447.Google Scholar
Nguyen, N.-Q. & Ladd, A. J. C. 2002 Lubrication corrections for lattice-Boltzmann simulations of particle suspensions. Phys. Rev. E 66, 046708.Google Scholar
Ozel, A., Fede, P. & Simonin, O. 2013 Development of filtered Euler-Euler two-phase model for circulating fluidised bed: High resolution simulation, formulation and a priori analyses. Intl J. Multiphase Flow 55, 43–63.CrossRefGoogle Scholar
Ozel, A., Parmentier, J. F., Simonin, O. & Fede, P. 2010 A priori test of effective drag modeling for filtered two-fluid model simulation of circulating and dense gas–solid fluidized beds. In Proceedings of the 7th International Conference on Multiphase Flow (ICMF 2010). University of Florida.Google Scholar
Parmentier, J.-F., Simonin, O. & Delsart, O. 2012 A functional subgrid drift velocity model for filtered drag prediction in dense fluidized bed. AIChE J. 58 (4), 1084–1098.Google Scholar
Pepiot, P. & Desjardins, O. 2012 Numerical analysis of the dynamics of two- and three-dimensional fluidized bed reactors using an Euler–Lagrange approach. Powder Technol. 220, 104–121.CrossRefGoogle Scholar
Qian, Y. H., D’Humieres, D. & Lallemand, P. 1992 Lattice BGK for the Navier–Stokes equations. Europhys. Lett. 17, 479–484.CrossRefGoogle Scholar
Richardson, J. F. & Zaki, W. N. 1954 Sedimentation and fluidisation: Part I. Trans. Inst. Chem. Engrs 32, 35–53.Google Scholar
Rubinstein, G. J., Derksen, J. J. & Sundaresan, S. 2016 Lattice Boltzmann simulations of low-Reynolds-number flow past fluidized spheres: effect of Stokes number on drag force. J. Fluid Mech. 788, 576–601.Google Scholar
Schneiderbauer, S. & Pirker, S. 2014 Filtered and heterogeneity-based subgrid modifications for gas–solid drag and solid stresses in bubbling fluidized beds. AIChE J. 60 (3), 839–854.CrossRefGoogle Scholar
Somers, J. A. 1993 Direct simulation of fluid flow with cellular automata and the lattice-Boltzmann equation. Appl. Sci. Res. 51 (1–2), 127–133.Google Scholar
Tang, Y., Peters, E. A. J. F. & Kuipers, J. A. M. 2016 Direct numerical simulations of dynamic gas–solid suspensions. AIChE J. 62 (6), 1958–1969.Google Scholar
Tenneti, S., Garg, R. & Subramaniam, S. 2011 Drag law for monodisperse gas–solid systems using particle-resolved direct numerical simulation of flow past fixed assemblies of spheres. Intl J. Multiphase Flow 37, 1072–1092.CrossRefGoogle Scholar
Wang, J., van der Hoef, M. A. & Kuipers, J. A. M. 2009 Why the two-fluid model fails to predict the bed expansion characteristics of Geldart A particles in gas-fluidized beds: a tentative answer. Chem. Engng Sci. 64 (3), 622–625.Google Scholar
Wang, X., Liu, K. & You, C. 2011 Drag force model corrections based on nonuniform particle distributions in multi-particle systems. Powder Technol. 209, 112–118.Google Scholar
Wen, C. Y. & Yu, Y. H. 1966 Mechanics of fluidization. Chem. Eng. Prog. Symp. Ser. 62 (1), 100–111.Google Scholar
Xu, M., Ge, W. & Li, J. 2007 A discrete particle model for particle-fluid flow with considerations of sub-grid structures. Chem. Engng Sci. 62 (8), 2302–2308.Google Scholar
Zhou, G., Xiong, Q., Wang, L., Wang, X., Ren, X. & Ge, W. 2014 Structure-dependent drag in gas–solid flows studied with direct numerical simulation. Chem. Engng Sci. 116, 9–22.Google Scholar
Supplementary material: File

Rubinstein et al supplementary material 1

Rubinstein et al supplementary material

Download Rubinstein et al supplementary material 1(File)
File 91.6 KB