Hostname: page-component-76fb5796d-5g6vh Total loading time: 0 Render date: 2024-04-25T16:37:34.785Z Has data issue: false hasContentIssue false
  • English
  • Français

Large-scale vortices in rapidly rotating Rayleigh–Bénard convection

Published online by Cambridge University Press:  09 October 2014

Céline Guervilly ,
David W. Hughes  and
Chris A. Jones
Céline Guervilly*
Affiliation:
Department of Applied Mathematics, University of Leeds, Leeds LS2 9JT, UK
David W. Hughes
Affiliation:
Department of Applied Mathematics, University of Leeds, Leeds LS2 9JT, UK
Chris A. Jones
Affiliation:
Department of Applied Mathematics, University of Leeds, Leeds LS2 9JT, UK
*
†Email address for correspondence: c.guervilly@leeds.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

Using numerical simulations of rapidly rotating Boussinesq convection in a Cartesian box, we study the formation of long-lived, large-scale, depth-invariant coherent structures. These structures, which consist of concentrated cyclones, grow to the horizontal scale of the box, with velocities significantly larger than the convective motions. We vary the rotation rate, the thermal driving and the aspect ratio in order to determine the domain of existence of these large-scale vortices (LSV). We find that two conditions are required for their formation. 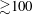First, the Rayleigh number, a measure of the thermal driving, must be several times its value at the linear onset of convection; this corresponds to Reynolds numbers, based on the convective velocity and the box depth, $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}{\gtrsim }100$. Second, the rotational constraint on the convective structures must be strong. This requires that the local Rossby number, based on the convective velocity and the horizontal convective scale, 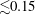${\lesssim }0.15$. Simulations in which certain wavenumbers are artificially suppressed in spectral space suggest that the LSV are produced by the interactions of small-scale, depth-dependent convective motions. The presence of LSV significantly reduces the efficiency of the convective heat transport.

JFM classification

Turbulent Flows: Rotating turbulence Turbulent Flows: Turbulent convection Vortex Flows: Vortex dynamics
Type
Papers
Information
Journal of Fluid Mechanics , Volume 758 , 10 November 2014 , pp. 407 - 435
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bartello, P., Metais, O. & Lesieur, M. 1994 Coherent structures in rotating three-dimensional turbulence. J. Fluid Mech. 273, 1–30.CrossRefGoogle Scholar
Boffetta, G. & Ecke, R. E. 2012 Two-dimensional turbulence. Annu. Rev. Fluid Mech. 44, 427–451.CrossRefGoogle Scholar
Boubnov, B. M. & Golitsyn, G. S. 1986 Experimental study of convective structures in rotating fluids. J. Fluid Mech. 167, 503–531.CrossRefGoogle Scholar
Busse, F. H. 1994 Convection driven zonal flows and vortices in the major planets. Chaos 4, 123–134.CrossRefGoogle ScholarPubMed
Cattaneo, F., Emonet, T. & Weiss, N. O. 2003 On the interaction between convection and magnetic fields. Astrophys. J. 588, 1183–1198.CrossRefGoogle Scholar
Cerretelli, C. & Williamson, C. H. K. 2003 The physical mechanism for vortex merging. J. Fluid Mech. 475, 41–77.CrossRefGoogle Scholar
Chan, K. L. 2007 Rotating convection in f-boxes: faster rotation. Astron. Nachr. 328, 1059–1061.CrossRefGoogle Scholar
Chan, K. L. & Mayr, H. G. 2013 Numerical simulation of convectively generated vortices: application to the Jovian planets. Earth Planet. Sci. Lett. 371, 212–219.CrossRefGoogle Scholar
Chandrasekhar, S. 1961 Hydrodynamic and Hydromagnetic Stability. Clarendon.Google Scholar
Chen, R., Fernando, H. J. S. & Boyer, D. L. 1989 Formation of isolated vortices in a rotating convecting fluid. J. Geophys. Res. 94, 18445–18453.CrossRefGoogle Scholar
Christensen, U. R. 2002 Zonal flow driven by strongly supercritical convection in rotating spherical shells. J. Fluid Mech. 470, 115–133.CrossRefGoogle Scholar
Favier, B., Silvers, L. J. & Proctor, M. R. E. 2014 Inverse cascade and symmetry breaking in rapidly-rotating Boussinesq convection. Phys. Fluids 26, 096605.CrossRefGoogle Scholar
Frisch, U., She, Z. S. & Sulem, P. L. 1987 Large-scale flow driven by the anisotropic kinetic alpha effect. Physica D 28, 382–392.CrossRefGoogle Scholar
Griffiths, R. W. & Hopfinger, E. J. 1987 Coalescing of geostrophic vortices. J. Fluid Mech. 178, 73–97.CrossRefGoogle Scholar
Heimpel, M., Aurnou, J. & Wicht, J. 2005 Simulation of equatorial and high-latitude jets on Jupiter in a deep convection model. Nature 438, 193–196.CrossRefGoogle Scholar
Hopfinger, E. J., Browand, F. K. & Gagne, Y. 1982 Turbulence and waves in a rotating tank. J. Fluid Mech. 125, 505–534.CrossRefGoogle Scholar
Hopfinger, E. J. & van Heijst, G. J. F. 1993 Vortices in rotating fluids. Annu. Rev. Fluid Mech. 25, 241–289.CrossRefGoogle Scholar
Julien, K., Legg, S., McWilliams, J. & Werne, J. 1996 Rapidly rotating turbulent Rayleigh–Bénard convection. J. Fluid Mech. 322, 243–273.CrossRefGoogle Scholar
Julien, K., Rubio, A. M., Grooms, I. & Knobloch, E. 2012 Statistical and physical balances in low Rossby number Rayleigh–Bénard convection. Geophys. Astrophys. Fluid Dyn. 106, 392–428.CrossRefGoogle Scholar
Käpylä, P. J., Mantere, M. J. & Hackman, T. 2011 Starspots due to large-scale vortices in rotating turbulent convection. Astrophys. J. 742, 34–41.CrossRefGoogle Scholar
King, E. M. & Aurnou, J. M. 2012 Thermal evidence for Taylor columns in turbulent rotating Rayleigh–Bénard convection. Phys. Rev. E 85, 016313.CrossRefGoogle ScholarPubMed
King, E. M., Stellmach, S. & Aurnou, J. M. 2012 Heat transfer by rapidly rotating Rayleigh–Bénard convection. J. Fluid Mech. 691, 568–582.CrossRefGoogle Scholar
Kraichnan, R. H. 1967 Inertial ranges in two-dimensional turbulence. Phys. Fluids 10, 1417–1423.CrossRefGoogle Scholar
Lesieur, M., Yanase, S. & Métais, O. 1991 Stabilizing and destabilizing effects of a solid-body rotation on quasi-two-dimensional shear layers. Phys. Fluids A 3, 403–407.CrossRefGoogle Scholar
Liu, Y. & Ecke, R. E. 1999 Nonlinear traveling waves in rotating Rayleigh–Bénard convection: stability boundaries and phase diffusion. Phys. Rev. E 59, 4091–4105.CrossRefGoogle Scholar
Mantere, M. J., Käpylä, P. J. & Hackman, T. 2011 Dependence of the large-scale vortex instability on latitude, stratification, and domain size. Astron. Nachr. 332, 876–882.CrossRefGoogle Scholar
McWilliams, J. C. 1984 The emergence of isolated coherent vortices in turbulent flow. J. Fluid Mech. 146, 21–43.CrossRefGoogle Scholar
Melander, M. V., Zabusky, N. J. & McWilliams, J. C. 1988 Symmetric vortex merger in two dimensions: causes and conditions. J. Fluid Mech. 195, 303–340.CrossRefGoogle Scholar
Meunier, P., Le Dizès, S. & Leweke, T. 2005 Physics of vortex merging. C. R. Phys. 6, 431–450.CrossRefGoogle Scholar
Morize, C., Moisy, F. & Rabaud, M. 2005 Decaying grid-generated turbulence in a rotating tank. Phys. Fluids 17, 095105.CrossRefGoogle Scholar
Özuğurlu, E., Reinaud, J. N. & Dritschel, D. G. 2008 Interaction between two quasi-geostrophic vortices of unequal potential vorticity. J. Fluid Mech. 597, 395–414.CrossRefGoogle Scholar
Rubio, A. M., Julien, K., Knobloch, E. & Weiss, J. B. 2014 Upscale energy transfer in three-dimensional rapidly rotating turbulent convection. Phys. Rev. Lett. 112, 144501.CrossRefGoogle ScholarPubMed
Schmitz, S. & Tilgner, A. 2009 Heat transport in rotating convection without Ekman layers. Phys. Rev. E 80, 015305.CrossRefGoogle ScholarPubMed
Schmitz, S. & Tilgner, A. 2010 Transitions in turbulent rotating Rayleigh–Bénard convection. Geophys. Astrophys. Fluid Dyn. 104, 481–489.CrossRefGoogle Scholar
Sprague, M., Julien, K., Knobloch, E. & Werne, J. 2006 Numerical simulation of an asymptotically reduced system for rotationally constrained convection. J. Fluid Mech. 551, 141–174.CrossRefGoogle Scholar
Staplehurst, P. J., Davidson, P. A. & Dalziel, S. B. 2008 Structure formation in homogeneous freely decaying rotating turbulence. J. Fluid Mech. 598, 81–105.CrossRefGoogle Scholar
Stellmach, S. & Hansen, U. 2004 Cartesian convection driven dynamos at low Ekman number. Phys. Rev. E 70, 056312.CrossRefGoogle ScholarPubMed
Vorobieff, P. & Ecke, R. E. 2002 Turbulent rotating convection: an experimental study. J. Fluid Mech. 458, 191–218.CrossRefGoogle Scholar
Yasuda, I. & Flierl, G. R. 1997 Two-dimensional asymmetric vortex merger: merger dynamics and critical merger distance. Dyn. Atmos. Oceans 26, 159–181.CrossRefGoogle Scholar
Zhong, J.-Q., Stevens, R. J. A. M., Clercx, H. J. H., Verzicco, R., Lohse, D. & Ahlers, G. 2009 Prandtl-, Rayleigh-, and Rossby-number dependence of heat transport in turbulent rotating Rayleigh–Bénard convection. Phys. Rev. Lett. 102, 044502.Google ScholarPubMed
Supplementary material: PDF

Guervilly et al. supplementary movie

Movie captions

Download Guervilly et al. supplementary movie(PDF)
PDF 24.9 KB

Guervilly et al. supplementary movie

See pdf file

Download Guervilly et al. supplementary movie(Video)
Video 8.7 MB

Guervilly et al. supplementary movie

See pdf file

Download Guervilly et al. supplementary movie(Video)
Video 8.6 MB