Article contents
A Lagrangian study of turbulent mixing: forward and backward dispersion of molecular trajectories in isotropic turbulence
Published online by Cambridge University Press: 23 June 2016
Abstract
Statistics of the trajectories of molecules diffusing via Brownian motion in a turbulent flow are extracted from simulations of stationary isotropic turbulence, using a postprocessing approach applicable in both forward and backward reference frames. Detailed results are obtained for Schmidt numbers (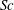 $Sc$) from 0.001 to 1000 at Taylor-scale Reynolds numbers up to 1000. The statistics of displacements of single molecules compare well with the earlier theoretical work of Saffman (J. Fluid Mech. vol. 8, 1960, pp. 273–283) except for the scaling of the integral time scale of the fluid velocity following the molecular trajectories. For molecular pairs we extend Saffman’s theory to include pairs of small but finite initial separation, which is in excellent agreement with numerical results provided that data are collected at sufficiently small times. At intermediate times the separation statistics of molecular pairs exhibit a more robust Richardson scaling behaviour than for the fluid particles. The forward scaling constant is very close to 0.55, whereas the backward constant is approximately 1.53–1.57, with a weak Schmidt number dependence, although no scaling exists if
$Sc$) from 0.001 to 1000 at Taylor-scale Reynolds numbers up to 1000. The statistics of displacements of single molecules compare well with the earlier theoretical work of Saffman (J. Fluid Mech. vol. 8, 1960, pp. 273–283) except for the scaling of the integral time scale of the fluid velocity following the molecular trajectories. For molecular pairs we extend Saffman’s theory to include pairs of small but finite initial separation, which is in excellent agreement with numerical results provided that data are collected at sufficiently small times. At intermediate times the separation statistics of molecular pairs exhibit a more robust Richardson scaling behaviour than for the fluid particles. The forward scaling constant is very close to 0.55, whereas the backward constant is approximately 1.53–1.57, with a weak Schmidt number dependence, although no scaling exists if 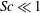 $Sc\ll 1$ at the Reynolds numbers presently accessible. An important innovation in this work is to demonstrate explicitly the practical utility of a Lagrangian description of turbulent mixing, where molecular displacements and separations in the limit of small backward initial separation can be used to calculate the evolution of scalar fluctuations resulting from a known source function in space. Lagrangian calculations of the production and dissipation rates of the scalar fluctuations are shown to agree very well with Eulerian results for the case of passive scalars driven by a uniform mean gradient. Although the Eulerian–Lagrangian comparisons are made only for
$Sc\ll 1$ at the Reynolds numbers presently accessible. An important innovation in this work is to demonstrate explicitly the practical utility of a Lagrangian description of turbulent mixing, where molecular displacements and separations in the limit of small backward initial separation can be used to calculate the evolution of scalar fluctuations resulting from a known source function in space. Lagrangian calculations of the production and dissipation rates of the scalar fluctuations are shown to agree very well with Eulerian results for the case of passive scalars driven by a uniform mean gradient. Although the Eulerian–Lagrangian comparisons are made only for  $Sc\sim O(1)$, the Lagrangian approach is more easily extended to both very low and very high Schmidt numbers. The well-known scalar dissipation anomaly is accordingly also addressed in a Lagrangian context.
$Sc\sim O(1)$, the Lagrangian approach is more easily extended to both very low and very high Schmidt numbers. The well-known scalar dissipation anomaly is accordingly also addressed in a Lagrangian context.
- Type
- Papers
- Information
- Copyright
- © 2016 Cambridge University Press
References
- 28
- Cited by



