Hostname: page-component-8448b6f56d-42gr6 Total loading time: 0 Render date: 2024-04-19T01:31:53.975Z Has data issue: false hasContentIssue false
  • English
  • Français

Intermittency in free vibration of a cylinder beyond the laminar regime

Published online by Cambridge University Press:  15 May 2019

Navrose Open the ORCID record for Navrose [Opens in a new window]  and
Sanjay Mittal Open the ORCID record for Sanjay Mittal [Opens in a new window]
Navrose
Affiliation:
Department of Aerospace Engineering, Indian Institute of Technology Kanpur, Kanpur 208 016, India
Sanjay Mittal*
Affiliation:
Department of Aerospace Engineering, Indian Institute of Technology Kanpur, Kanpur 208 016, India
*
†Email address for correspondence: smittal@iitk.ac.in
Get access Rights & Permissions [Opens in a new window]

Abstract

Vortex-induced vibration of a circular cylinder that is free to move in the transverse (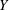$Y$) and streamwise (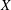$X$) directions is investigated at subcritical Reynolds numbers (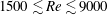$1500\lesssim Re\lesssim 9000$) via three-dimensional (3-D) numerical simulations. The mass ratio of the system for all the simulations is 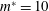$m^{\ast }=10$. It is observed that while some of the characteristics associated with the 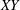$XY$-oscillation are similar to those of the $Y$-only oscillation (in line with the observations made by Jauvtis & Williamson (J. Fluid Mech., vol. 509, 2004, pp. 23–62)), notable differences exist between the two systems with respect to the transition between the branches of the cylinder response in the lock-in regime. The flow regime between the initial and lower branch is characterized by intermittent switching in the cylinder response, aerodynamic coefficients and modes of vortex shedding. Similar to the regime of laminar flow, the system exhibits a hysteretic response near the lower- and higher-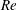$Re$ end of the lock-in regime. The frequency spectrum of time history of the cylinder response shows that the most dominant frequency in the streamwise oscillation on the initial branch is the same as that of the transverse oscillation.

JFM classification

Vortex Flows: Vortex shedding Wakes/Jets: Wakes
Type
JFM Rapids
Information
Journal of Fluid Mechanics , Volume 870 , 10 July 2019 , R2
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bearman, P. W. 2011 Circular cylinder wakes and vortex-induced vibrations. J. Fluids Struct. 27, 648–658.Google Scholar
Blackburn, H. M., Marques, F. & Lopez, J. M. 2005 Symmetry breaking of two-dimensional time-periodic wakes. J. Fluid Mech. 522, 395–411.Google Scholar
Bourguet, R. & Lo Jacono, D. 2015 In-line flow-induced vibrations of a rotating cylinder. J. Fluid Mech. 781, 127–165.Google Scholar
Govardhan, R. & Williamson, C. H. K. 2000 Modes of vortex formation and frequency response of a freely vibrating cylinder. J. Fluid Mech. 420, 85–130.Google Scholar
Govardhan, R. & Williamson, C. H. K. 2002 Resonance forever: existence of a critical mass and an infinite regime of resonance in vortex-induced vibration. J. Fluid Mech. 473, 147–166.Google Scholar
Govardhan, R. & Williamson, C. H. K. 2006 Defining the modified Griffin plot in vortex-induced vibration: revealing the effect of Reynolds number using controlled damping. J. Fluid Mech. 561, 147–180.Google Scholar
Jauvtis, N. & Williamson, C. H. K. 2004 The effect of two degrees of freedom on vortex-induced vibration at low mass and damping. J. Fluid Mech. 509, 23–62.Google Scholar
Khalak, A. & Williamson, C. H. K. 1999 Motions, forces and mode transitions in vortex-induced vibrations at low mass-damping. J. Fluids Struct. 13 (7), 813–851.Google Scholar
Lighthill, J. 1986 Wave loading on offshore structures. J. Fluid Mech. 173, 667–681.Google Scholar
Navrose & Mittal, S. 2013 Free vibrations of a cylinder: 3-D computations at Re = 1000. J. Fluids Struct. 41, 109–118.Google Scholar
Navrose & Mittal, S. 2017 The critical mass phenomenon in vortex-induced vibration at low Re . J. Fluid Mech. 820, 159–186.Google Scholar
Navrose, Yogeswaran, V., Sen, S. & Mittal, S. 2014 Free vibrations of an elliptic cylinder at low Reynolds numbers. J. Fluids Struct. 51, 55–67.Google Scholar
Prasanth, T. K. & Mittal, S. 2008 Vortex-induced vibrations of a circular cylinder at low Reynolds numbers. J. Fluid Mech. 594, 463–491.Google Scholar
Ryan, K. C., Thompson, M. C. & Hourigan, K. 2005 Variation in the critical mass ratio of a freely oscillating cylinder as a function of Reynolds number. Phys. Fluids 17 (3), 038106.Google Scholar
Sarpkaya, T. 2004 A critical review of the intrinsic nature of vortex-induced vibrations. J. Fluids Struct. 19, 389–447.Google Scholar
Singh, S. P. & Mittal, S. 2005 Vortex-induced oscillations at low Reynolds numbers: hysteresis and vortex-shedding modes. J. Fluids Struct. 20 (8), 1085–1104.Google Scholar
Williamson, C. H. K. & Govardhan, R. 2004 Vortex-induced vibrations. Annu. Rev. Fluid Mech. 36, 413–455.Google Scholar
Williamson, C. H. K. & Roshko, A. 1988 Vortex formation in the wake of an oscillating cylinder. J. Fluids Struct. 2 (4), 355–381.Google Scholar
Zhao, J., Leontini, J. S., Lo Jacono, D. & Sheridan, J. 2014 Chaotic vortex induced vibrations. Phys. Fluids 26 (12), 121702.Google Scholar