Hostname: page-component-848d4c4894-tn8tq Total loading time: 0 Render date: 2024-07-02T03:26:00.956Z Has data issue: false hasContentIssue false
  • English
  • Français

Insights into the periodic gust response of airfoils

Published online by Cambridge University Press:  31 July 2019

Nathaniel J. Wei Open the ORCID record for Nathaniel J. Wei [Opens in a new window] ,
Johannes Kissing Open the ORCID record for Johannes Kissing [Opens in a new window] ,
Tom T. B. Wester ,
Sebastian Wegt ,
Klaus Schiffmann ,
Suad Jakirlic ,
Michael Hölling ,
Joachim Peinke  and
Cameron Tropea
Nathaniel J. Wei
Affiliation:
Institute for Fluid Mechanics and Aerodynamics, Technische Universität Darmstadt, Flughafenstraße 19, 64347 Griesheim, Germany Department of Mechanical Engineering, Stanford University, Stanford, CA 94305, USA
Johannes Kissing
Affiliation:
Institute for Fluid Mechanics and Aerodynamics, Technische Universität Darmstadt, Flughafenstraße 19, 64347 Griesheim, Germany
Tom T. B. Wester
Affiliation:
ForWind, Institute of Physics, University of Oldenburg, Küpkersweg 70, 26129 Oldenburg, Germany
Sebastian Wegt
Affiliation:
Institute for Fluid Mechanics and Aerodynamics, Technische Universität Darmstadt, Flughafenstraße 19, 64347 Griesheim, Germany
Klaus Schiffmann
Affiliation:
Institute for Fluid Mechanics and Aerodynamics, Technische Universität Darmstadt, Flughafenstraße 19, 64347 Griesheim, Germany
Suad Jakirlic
Affiliation:
Institute for Fluid Mechanics and Aerodynamics, Technische Universität Darmstadt, Flughafenstraße 19, 64347 Griesheim, Germany
Michael Hölling
Affiliation:
ForWind, Institute of Physics, University of Oldenburg, Küpkersweg 70, 26129 Oldenburg, Germany
Joachim Peinke
Affiliation:
ForWind, Institute of Physics, University of Oldenburg, Küpkersweg 70, 26129 Oldenburg, Germany
Cameron Tropea*
Affiliation:
Institute for Fluid Mechanics and Aerodynamics, Technische Universität Darmstadt, Flughafenstraße 19, 64347 Griesheim, Germany
*
†Email address for correspondence: tropea@sla.tu-darmstadt.de
Get access Rights & Permissions [Opens in a new window]

Abstract

The unsteady lift response of an airfoil in a sinusoidal gust has in the past been modelled by two different transfer functions: the first-order Sears function and the second-order Atassi function. Previous studies have shown that the Sears function holds in experiments, but recently Cordes et al. (J. Fluid Mech., vol. 811, 2017) reported experimental data that corresponded to the Atassi function rather than the Sears function. In order to clarify the observed discrepancy, the specific differences between these models are isolated analytically. To this end, data and analysis are confined to unloaded airfoils. These differences are related to physical gust parameters, and gusts with these parameters are then produced in wind-tunnel experiments using an active-grid gust generator. Measurements of the unsteady gust loads on an airfoil in the wind tunnel at Reynolds numbers (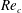$Re_{c}$) of 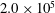$2.0\times 10^{5}$ and 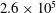$2.6\times 10^{5}$ and reduced frequencies between 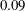$0.09$ and 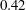$0.42$ confirm that the Sears and Atassi functions differ only in convention: the additional gust component of the Atassi problem can be scaled so that the Atassi function collapses onto the Sears function. These experiments, complemented by numerical simulations of the set-up, validate both models across a range of gust parameters. Finally, the influence of boundary-layer turbulence and the turbulent wake of the gust generator on experimental convergence with model predictions is investigated. These results serve to clarify the conditions under which the Sears and Atassi functions can be applied, and demonstrate that the Sears function can effectively model unsteady forces even when significant fluctuations in the streamwise velocity are present.

JFM classification

Aerodynamics: Aerodynamics
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 876 , 10 October 2019 , pp. 237 - 263
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Atassi, H. M. 1984 The Sears problem for a lifting airfoil revisited – new results. J. Fluid Mech. 141, 109–122.Google Scholar
Billah, K. Y. & Scanlan, R. H. 1991 Resonance, Tacoma Narrows bridge failure, and undergraduate physics textbooks. Am. J. Phys. 59 (2), 118–124.Google Scholar
Commerford, G. L. & Carta, F. O. 1974 Unsteady aerodynamic response of a two-dimensional airfoil at high reduced frequency. AIAA J. 12 (1), 43–48.Google Scholar
Cordes, U., Kampers, G., Meißner, T., Tropea, C., Peinke, J. & Hölling, M. 2017 Note on the limitations of the Theodorsen and Sears functions. J. Fluid Mech. 811, R1.Google Scholar
Drela, M. 1989 XFOIL: an analysis and design system for low Reynolds number airfoils. In Low Reynolds Number Aerodynamics, pp. 1–12. Springer.Google Scholar
Goldstein, M. E. & Atassi, H. 1976 A complete second-order theory for the unsteady flow about an airfoil due to a periodic gust. J. Fluid Mech. 74 (4), 741–765.Google Scholar
Greenberg, J. M.1947 Airfoil in sinusoidal motion in a pulsating stream. NACA Tech. Note 1326.Google Scholar
Hakkinen, R. J. & Richardson, A. S.1957 Theoretical and experimental investigation of random gust loads Part I. Aerodynamic transfer function of a simple wing configuration in incompressible flow. NACA Tech. Note 3878.Google Scholar
Ham, N. D., Bauer, P. H. & Lawrence, T. L.1974 Wind tunnel generation of sinusoidal lateral and longitudinal gusts by circulation of twin parallel airfoils. NASA CR 137547. NASA.Google Scholar
Hatanaka, A. & Tanaka, H. 2002 New estimation method of aerodynamic admittance function. J. Wind Engng Ind. Aerodyn. 90 (12), 2073–2086.Google Scholar
Jakirlic, S. & Hanjalic, K. 2002 A new approach to modelling near-wall turbulence energy and stress dissipation. J. Fluid Mech. 459, 139–166.Google Scholar
Jakirlić, S. & Maduta, R. 2015 Extending the bounds of ‘steady’ RANS closures: toward an instability-sensitive Reynolds stress model. Intl J. Heat Fluid Flow 51, 175–194.Google Scholar
Jancauskas, E. D. & Melbourne, W. H. 1983 The aerodynamic admittance of a slender box girder bridge section. In Proceedings of the 8th Australasian Fluid Mechanics Conference, Newcastle, Australia. University of Newcastle, N.S.W., 11B.1–11B.4.Google Scholar
Jancauskas, E. D. & Melbourne, W. H. 1986 The aerodynamic admittance of two-dimensional rectangular section cylinders in smooth flow. J. Wind Engng Ind. Aerodyn. 23, 395–408.Google Scholar
Knebel, P., Kittel, A. & Peinke, J. 2011 Atmospheric wind field conditions generated by active grids. Exp. Fluids 51 (2), 471–481.Google Scholar
Lancelot, P. M. G. J., Sodja, J., Werter, N. P. M. & De Breuker, R. 2015 Design and testing of a low subsonic wind tunnel gust generator. In Proceedings of the 16th International Forum on Aeroelasticity and Structural Dynamics, IFASD 2015, St. Petersburg (Russia), 28 June–2 July, 2015; Author’s version. Central Aerohydrodynamic Institute (TsAGI).Google Scholar
Larose, G. L. 1999 Experimental determination of the aerodynamic admittance of a bridge deck segment. J. Fluids Struct. 13 (7), 1029–1040.Google Scholar
Leishman, G. J. 2006 Principles of Helicopter Aerodynamics, 2nd edn. Cambridge University Press.Google Scholar
Lysak, P. D., Capone, D. E. & Jonson, M. L. 2013 Prediction of high frequency gust response with airfoil thickness effects. J. Fluids Struct. 39 (Supplement C), 258–274.Google Scholar
Lysak, P. D., Capone, D. E. & Jonson, M. L. 2016 Measurement of the unsteady lift of thick airfoils in incompressible turbulent flow. J. Fluids Struct. 66, 315–330.Google Scholar
Maduta, R., Ullrich, M. & Jakirlic, S. 2017 Reynolds stress modelling of wake interference of two cylinders in tandem: conventional vs. eddy-resolving closure. Intl J. Heat Fluid Flow 67, 139–148.Google Scholar
Massaro, M. & Graham, J. M. R. 2015 The effect of three-dimensionality on the aerodynamic admittance of thin sections in free stream turbulence. J. Fluids Struct. 57 (Supplement C), 81–90.Google Scholar
Menter, F. R. & Egorov, Y. 2010 The scale-adaptive simulation method for unsteady turbulent flow predictions. Part 1: Theory and model description. Flow Turbul. Combust. 85 (1), 113–138.Google Scholar
Popovac, M. & Hanjalic, K. 2007 Compound wall treatment for rans computation of complex turbulent flows and heat transfer. Flow Turbul. Combust. 78 (2), 177–202.Google Scholar
Reynolds, K. V., Thomas, A. L. R. & Taylor, G. K. 2014 Wing tucks are a response to atmospheric turbulence in the soaring flight of the steppe eagle Aquila nipalensis. J. R. Soc. Interface 11 (101), 20140645.Google Scholar
Sankaran, R. & Jancauskas, E. D. 1992 Direct measurement of the aerodynamic admittance of two-dimensional rectangular cylinders in smooth and turbulent flows. J. Wind Engng Ind. Aerodyn. 41 (1), 601–611.Google Scholar
Sears, W. R.1938 A systematic presentation of the theory of thin airfoils in non-uniform motion. PhD dissertation, California Institute of Technology, Pasadena, CA.Google Scholar
Sears, W. R. 1941 Some aspects of non-stationary airfoil theory and its practical application. J. Aeronaut. Sci. 8 (3), 104–108.Google Scholar
Spinato, F., Tavner, P. J., Van Bussel, G. J. W. & Koutoulakos, E. 2009 Reliability of wind turbine subassemblies. IET Renew. Power Generation 3 (4), 387–401.Google Scholar
Theodorsen, T.1934 General theory of aerodynamic instability and the mechanism of flutter. NACA Tech. Rep. 496.Google Scholar
Traphan, D., Wester, T. T. B., Peinke, J. & Gülker, G. 2018 On the aerodynamic behavior of an airfoil under tailored turbulent inflow conditions. In Proceedings of the 5th International Conference on Experimental Fluid Mechanics, Munich, Germany. Universität der Bundeswehr München.Google Scholar
von Kármán, T. 1938 Airfoil theory for non-uniform motion. J. Aeronaut. Sci. 5 (10), 379–390.Google Scholar
Wang, J., Wang, K. & Wang, M. 2017 Large-eddy simulation study of rotor noise generation in a turbulent wake. In 23rd AIAA/CEAS Aeroacoustics Conference, Denver, Colorado, USA. American Institute of Aeronautics and Astronautics.Google Scholar
Wegt, S.2017 Numerische Modellierung der Tragflügelaerodynamik unter Bedingungen böiger Anströmung. Master’s thesis, Technische Universität Darmstadt.Google Scholar
Zarovy, S., Costello, M., Mehta, A., Gremillion, G., Miller, D., Ranganathan, B., Humbert, J. S. & Samuel, P. 2010 Experimental study of gust effects on micro air vehicles. In AIAA Atmospheric Flight Mechanics Conference. American Institute of Aeronautics and Astronautics.Google Scholar
Zhao, X., Gouder, K., Graham, J. M. R. & Limebeer, D. J. N. 2016 Buffet loading, dynamic response and aerodynamic control of a suspension bridge in a turbulent wind. J. Fluids Struct. 62, 384–412.Google Scholar