Hostname: page-component-77c89778f8-vsgnj Total loading time: 0 Render date: 2024-07-20T15:07:44.589Z Has data issue: false hasContentIssue false
  • English
  • Français

The influence of surfactant on the propagation of a semi-infinite bubble through a liquid-filled compliant channel

Published online by Cambridge University Press:  30 March 2012

David Halpern  and
Donald P. Gaver III
David Halpern*
Affiliation:
Department of Mathematics, University of Alabama, Tuscaloosa, AL 35487, USA
Donald P. Gaver III
Affiliation:
Department of Biomedical Engineering, Tulane University, New Orleans, LA 70130, USA
*
†Email address for correspondence: dhalpern@as.ua.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate the influence of a soluble surfactant on the steady-state motion of a finger of air through a compliant channel. This study provides a basic model from which to understand the fluid–structure interactions and physicochemical hydrodynamics of pulmonary airway reopening. Airway closure occurs in lung diseases such as respiratory distress syndrome and acute respiratory distress syndrome as a result of fluid accumulation and surfactant insufficiency. This results in ‘compliant collapse’ with the airway walls buckled and held in apposition by a liquid occlusion that blocks the passage of air. Airway reopening is essential to the recovery of adequate ventilation, but has been associated with ventilator-induced lung injury because of the exposure of airway epithelial cells to large interfacial flow-induced pressure gradients. Surfactant replacement is helpful in modulating this deleterious mechanical stimulus, but is limited in its effectiveness owing to slow surfactant adsorption. We investigate the effect of surfactant on micro-scale models of reopening by computationally modelling the steady two-dimensional motion of a semi-infinite bubble propagating through a liquid-filled compliant channel doped with soluble surfactant. Many dimensionless parameters affect reopening, but we primarily investigate how the reopening pressure 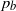depends upon the capillary number (the ratio of viscous to surface tension forces), the adsorption depth parameter 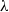(a bulk concentration parameter) and the bulk Péclet number 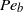(the ratio of bulk convection to diffusion). These studies demonstrate a dependence of 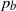on 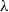, and suggest that a critical bulk concentration must be exceeded to operate as a low-surface-tension system. Normal and tangential stress gradients remain largely unaffected by physicochemical interactions – for this reason, further biological studies are suggested that will clarify the role of wall flexibility and surfactant on the protection of the lung from atelectrauma.

JFM classification

Biological Fluid Dynamics: Biomedical flows Biological Fluid Dynamics: Pulmonary fluid mechanics
Type
Papers
Information
Journal of Fluid Mechanics , Volume 698 , 10 May 2012 , pp. 125 - 159
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Amin, S. D. & Suki, B. 2012 Could dynamic ventilation waveforms bring about a paradigm shift in mechanical ventilation? J. Appl. Physiol. 112 (3), 333–334.CrossRefGoogle ScholarPubMed
2. Bilek, A. M., Dee, K. C. & Gaver, D. P. 2003 Mechanisms of surface-tension-induced epithelial cell damage in a model of pulmonary airway reopening. J. Appl. Physiol. 94, 770–783.CrossRefGoogle Scholar
3. Ferri, J. K. & Stebe, K. J. 2000 Which surfactants reduce surface tension faster? A scaling argument for diffusion-controlled adsorption. Adv. Colloid Interface Sci. 85, 61–97.CrossRefGoogle ScholarPubMed
4. Fletcher, C. A. J. & Srinivas, K. 1991 Computational Techniques for Fluid Dynamics. Springer.Google Scholar
5. Gaver, D. P. III, Halpern, D. & Jensen, O. E. 2005 Surfactant and airway liquid flows. In Lung Surfactant Function and Disorder (ed. Nag, K. ). Taylor & Francis.Google Scholar
6. Gaver, D. P. III, Halpern, D., Jensen, O. E. & Grotberg, J. B. 1996 The steady motion of a semi-infinite bubble through a flexible-walled channel. J. Fluid Mech. 319, 25–65.CrossRefGoogle Scholar
7. Gaver, D. P. III, Jacob, A. M., Bilek, A. M. & Dee, K. C. 2006 The significance of air–liquid interfacial stresses on low-volume ventilator-induced lung injury. In Ventilator-Induced Lung Injury (ed. Dreyfuss, D., Saumon, G. & Hubmayr, R. D. ). Taylor & Francis.Google Scholar
8. Gaver, D. P. III, Samsel, R. W. & Solway, J. 1990 Effects of surface tension and viscosity on airway reopening. J. Appl. Physiol. 69, 74–85.CrossRefGoogle ScholarPubMed
9. Ghadiali, S. N. & Gaver, D. P. III. 2000 An investigation of pulmonary surfactant physicochemical behaviour under airway reopening conditions. J. Appl. Physiol. 88, 493–506.CrossRefGoogle ScholarPubMed
10. Ghadiali, S. N. & Gaver, D. P. III. 2001 A dual-reciprocity boundary element method for evaluating bulk convective transport of surfactant in free-surface flows. J. Comput. Phys. 171, 534–559.CrossRefGoogle Scholar
11. Ghadiali, S. N. & Gaver, D. P. III. 2003 The influence of non-equilibrium surfactant dynamics on the flow of a semi-infinite bubble in a rigid cylindrical tube. J. Fluid Mech. 478, 165–196.CrossRefGoogle Scholar
12. Glindmeyer, H. W. IV, Smith, B. J. & Gaver, D. P. III. 2012 In situ enhancement of pulmonary surfactant function using temporary flow reversal. J. Appl. Physiol. 112, 149–158.CrossRefGoogle ScholarPubMed
13. Halpern, D., Fujioka, H., Takayama, S. & Grotberg, J. B. 2008 Liquid and surfactant delivery into pulmonary airways. Respir. Physiol. Neurobiol. 163, 222–231.CrossRefGoogle ScholarPubMed
14. Halpern, D. & Gaver, D. P. 1994 Boundary-element analysis of the time-dependent motion of a semiinfinite bubble in a channel. J. Comput. Phys. 115, 366–375.CrossRefGoogle Scholar
15. Halpern, D., Naire, S., Jensen, O. E. & Gaver, D. P. III. 2005 Unsteady bubble propagation in a flexible channel: predictions of a viscous stick–slip instability. J. Fluid Mech. 528, 53–86.CrossRefGoogle Scholar
16. Hazel, A. L. & Heil, M. 2003 Three-dimensional airway reopening: the steady propagation of a semi-infinite bubble into a buckled elastic tube. J. Fluid Mech. 478, 47–70.CrossRefGoogle Scholar
17. Hazel, A. L. & Heil, M. 2008 The influence of gravity on the steady propagation of a semi-infinite bubble into a flexible channel. Phys. Fluids 20.CrossRefGoogle Scholar
18. Heil, M. 2000 Finite Reynolds number effects in the propagation of an air finger into a liquid-filled flexible-walled channel. J. Fluid Mech. 424, 21–44.CrossRefGoogle Scholar
19. Heil, M., Hazel, A. L. & Smith, J. A. 2008 Mechanics of airway closure. Respir. Physiol. Neurobiol. 163, 214–221.CrossRefGoogle ScholarPubMed
20. Hubmayr, R. D. 2002 Perspective on lung injury and recruitment: a skeptical look at the opening and collapse story. Am. J. Respir. Crit. Care Med. 165, 1647–1653.CrossRefGoogle Scholar
21. Huh, D., Fujioka, H., Tung, Y. C., Futai, N., Paine, R. 3rd, Grotberg, J. B. & Takayama, S. 2007 Acoustically detectable cellular-level lung injury induced by fluid mechanical stresses in microfluidic airway systems. Proc. Natl Acad. Sci. USA 104, 18 886–18 891.CrossRefGoogle ScholarPubMed
22. Jacob, A. M. & Gaver, D. P. III. 2005 An investigation of the influence of cell topography on epithelial mechanical stresses during pulmonary airway reopening. Phys. Fluids 17 (3), 031502.CrossRefGoogle ScholarPubMed
23. Jensen, O. E., Horsburgh, M. K., Halpern, D. & Gaver, D. P. 2002 The steady propagation of a bubble in a flexible-walled channel: asymptotic and computational models. Phys. Fluids 14, 443–457.CrossRefGoogle Scholar
24. Juel, A. & Heap, A. 2007 The reopening of a collapsed fluid-filled elastic tube. J. Fluid Mech. 572, 287–310.CrossRefGoogle Scholar
25. Kay, S. S., Bilek, A. M., Dee, K. C. & Gaver, D. P. 2004 Pressure gradient, not exposure duration, determines the extent of epithelial cell damage in a model of pulmonary airway reopening. J. Appl. Physiol. 97, 269–276.CrossRefGoogle ScholarPubMed
26. Krueger, M. A. & Gaver, D. P. III. 2000 A theoretical model of pulmonary surfactant multilayer collapse under oscillating area conditions. J. Colloid Interface Sci. 229, 353–364.CrossRefGoogle ScholarPubMed
27. Lambert, R. K., Wilson, T. A., Hyatt, R. E. & Rodarte, J. R. 1982 A computational model for expiratory flow. J. Appl. Physiol. 52, 44–56.CrossRefGoogle ScholarPubMed
28. Naire, S. & Jensen, O. E. 2005 Epithelial cell deformation during surfactant-mediated airway reopening: a theoretical model. J. Appl. Physiol. 99, 458–471.CrossRefGoogle ScholarPubMed
29. Notter, R. H. 2000 Lung Surfactants – Basic Science and Clinical Applications. Marcel Dekker.CrossRefGoogle Scholar
30. Overby, D. R. 1997 A computational investigation of pulmonary airway reopening, Master of Science in Engineering. Tulane University.Google Scholar
31. Patankar, S. V. 1980 Numerical Heat Transfer and Fluid FLow. Hemisphere.Google Scholar
32. Perun, M. L. & Gaver, D. P. 3rd. 1995a An experimental model investigation of the opening of a collapsed untethered pulmonary airway. Trans. ASME: J. Biomech. Engng 117, 245–253.Google ScholarPubMed
33. Perun, M. L. & Gaver, D. P. 3rd. 1995b Interaction between airway lining fluid forces and parenchymal tethering during pulmonary airway reopening. J. Appl. Physiol. 79, 1717–1728.CrossRefGoogle ScholarPubMed
34. Pillert, J. E. & Gaver, D. 2009 Physicochemical effects enhance surfactant transport in pulsatile motion of a semi-infinite bubble. Biophys. J. 96, 312–327.CrossRefGoogle ScholarPubMed
35. Rubenfeld, G. D., Caldwell, E., Peabody, E., Weaver, J., Martin, D. P., Neff, M., Stern, E. J. & Hudson, L. D. 2005 Incidence and outcomes of acute lung injury. New Engl. J. Med. 353, 1685–1693.CrossRefGoogle ScholarPubMed
36. Smith, B. J. & Gaver, D. P. 2008 The pulsatile propagation of a finger of air within a fluid-occluded cylindrical tube. J. Fluid Mech. 601, 1–23.CrossRefGoogle ScholarPubMed
37. Smith, B. J., Lukens, S., Yamaguchi, E. & Gaver, D. P. III. 2012 Lagrangian transport properties of pulmonary interfacial flows. J. Fluid Mech. doi:10.1017/jfm.2011.391.CrossRefGoogle Scholar
38. Stebe, K. J. & Bartes-Biesel, D. 1995 Marangoni effects of adsorption–desorption controlled surfactants on the leading end of an infinitely long bubble in a capillary. J. Fluid Mech. 286, 25–48.CrossRefGoogle Scholar
39. Stebe, K. J., Lin, S.-Y. & Maldarelli, C. 1991 Remobilizing surfactant retarded fluid particle interfaces. I. Stress-free conditions at the interfaces of micellar solutions of surfactants with fast sorption kinetics. Phys. Fluids. A, Fluid Dyn. 3, 3–20.CrossRefGoogle Scholar
40. Stebe, K. J. & Maldarelli, C. 1994 Remobilizing surfactant retarded fluid particle interfaces. II. Controlling the surface mobility at interfaces of solution containing surface active components. J. Colloid Interface Sci. 163, 177–189.CrossRefGoogle Scholar
41. Thompson, J. F., Soni, B. K. & Weatherill, N. P. 1999 Handbook of Grid Generation. CRC Press.Google Scholar
42. Yalcin, H. C., Perry, S. F. & Ghadiali, S. N. 2007 Influence of airway diameter and cell confluence on epithelial cell injury in an in-vitro model of airway reopening. J. Appl. Physiol. 103, 1796–1807.CrossRefGoogle Scholar
43. Yap, D. Y. K. & Gaver, D. P. 1998 The influence of surfactant on two-phase flow in a flexible- walled channel under bulk equilibrium conditions. Phys. Fluids 10, 1846–1863.CrossRefGoogle Scholar
44. Zasadzinski, J. A., Stenger, P. C., Shieh, I. & Dhar, P. 2010 Overcoming rapid inactivation of lung surfactant: analogies between competitive adsorption and colloid stability. Biochim. Biophys. Acta. 1798, 801–828.CrossRefGoogle ScholarPubMed
45. Zimmer, M. E. IV, Williams, H. A. R. & Gaver, D. P. III. 2005 The pulsatile motion of a semi-infinite bubble in a channel: flow field, and transport of an inactive surface-associated contaminant. J. Fluid Mech. 537, 1–33.CrossRefGoogle Scholar