Hostname: page-component-76fb5796d-dfsvx Total loading time: 0 Render date: 2024-04-25T13:29:16.737Z Has data issue: false hasContentIssue false
  • English
  • Français

The influence of shear on double-diffusive and settling-driven instabilities

Published online by Cambridge University Press:  26 June 2018

N. Konopliv ,
L. Lesshafft Open the ORCID record for L. Lesshafft [Opens in a new window]  and
E. Meiburg Open the ORCID record for E. Meiburg [Opens in a new window]
N. Konopliv
Affiliation:
Department of Mechanical Engineering, University of California, Santa Barbara, CA 93106, USA
L. Lesshafft
Affiliation:
Laboratoire d’Hydrodynamique, CNRS – École Polytechnique, 91128 Palaiseau, France
E. Meiburg*
Affiliation:
Department of Mechanical Engineering, University of California, Santa Barbara, CA 93106, USA
*
†Email address for correspondence: meiburg@engineering.ucsb.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

The effects of shear on double-diffusive fingering and on the settling-driven instability are assessed by means of a transient growth analysis. Employing Kelvin waves within a linearized framework allows for the consideration of time-dependent waveforms in uniform shear. In this way, the effects of boundaries and of shear-driven instability modes can be eliminated, so that the influence of shear on the double-diffusive and settling-driven instabilities can be analysed in isolation. Shear is seen to dampen both instabilities, which is consistent with previous findings by other authors. The shear damping is more pronounced for parameter values that produce larger unsheared growth. These trends can be explained in terms of instantaneous linear stability results for the unsheared case. For both double-diffusive and settling-driven instabilities, low Prandtl number (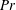$Pr$) values result in less damping and an increased importance of the Orr mechanism, for which a quantitative scaling law is obtained.

JFM classification

Convection: Double diffusive convection Geophysical and Geological Flows: Sediment transport Geophysical and Geological Flows: Stratified flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 849 , 25 August 2018 , pp. 902 - 926
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alsinan, A., Meiburg, E. & Garaud, P. 2017 A settling-driven instability in two-component, stably stratified fluids. J. Fluid Mech. 816, 243–267.Google Scholar
Burns, P. & Meiburg, E. 2012 Sediment-laden fresh water above salt water: linear stability analysis. J. Fluid Mech. 691, 279–314.Google Scholar
Burns, P. & Meiburg, E. 2015 Sediment-laden fresh water above salt water: nonlinear simulations. J. Fluid Mech. 762, 156–195.Google Scholar
Craik, A. D. D. & Criminale, W. O. 1986 Evolution of wavelike disturbances in shear flows: a class of exact solutions of the Navier–Stokes equations. Proc. R. Soc. Lond. A 406 (1830), 13–26.Google Scholar
Drazin, P. G. & Reid, W. H. 1981 Hydrodynamic Stability. Cambridge University Press.Google Scholar
Gunzburger, M. 2000 Adjoint equation-based methods for control problems in incompressible, viscous flows. Flow Turbul. Combust. 65 (3), 249–272.Google Scholar
Howard, L. N. 1961 Note on a paper of john w. miles. J. Fluid Mech. 10 (4), 509–512.Google Scholar
Kelvin, L. 1887 Stability of fluid motion: rectilinear motion of viscous fluid between two parallel plates. Phil. Mag. 24 (5), 188–196.Google Scholar
Knobloch, E. 1984 On the stability of stratified plane Couette flow. Geophys. Astrophys. Fluid Dyn. 29 (1–4), 105–116.Google Scholar
Linden, P. F. 1974 Salt fingers in a steady shear flow. Geophys. Astrophys. Fluid Dyn. 6 (1), 1–27.Google Scholar
Lindzen, R. S. 1988 Instability of plane parallel shear flow (toward a mechanistic picture of how it works). Pure Appl. Geophys. 126 (1), 103–121.Google Scholar
Radko, T. 2013 Double-Diffusive Convection. Cambridge University Press.Google Scholar
Radko, T., Ball, J., Colosi, J. & Flanagan, J. 2015 Double-diffusive convection in a stochastic shear. J. Phys. Oceanogr. 45 (12), 3155–3167.Google Scholar
Reali, J. F., Garaud, P., Alsinan, A. & Meiburg, E. 2017 Layer formation in sedimentary fingering convection. J. Fluid Mech. 816, 268–305.Google Scholar
Rosen, G. 1971 General solution for perturbed plane Couette flow. Phys. Fluids 14 (12), 2767–2769.Google Scholar
Shepherd, T. G. 1985 Time development of small disturbances to plane Couette flow. J. Atmos. Sci. 42 (17), 1868–1872.Google Scholar
Smyth, W. D. & Kimura, S. 2007 Instability and diapycnal momentum transport in a double-diffusive, stratified shear layer. J. Phys. Oceanogr. 37, 1551–1565.Google Scholar
Smyth, W. D. & Kimura, S. 2011 Mixing in a moderately sheared salt-fingering layer. J. Phys. Oceanogr. 41, 1364–1384.Google Scholar
Yu, X., Hsu, T. & Balachandar, S. 2013 Convective instability in sedimentation: linear stability analysis. J. Geophys. Res. 118 (1), 256–272.Google Scholar
Yu, X., Hsu, T. & Balachandar, S. 2014 Convective instability in sedimentation: 3-d numerical study. J. Geophys. Res. 119 (11), 8141–8161.Google Scholar