Hostname: page-component-8448b6f56d-m8qmq Total loading time: 0 Render date: 2024-04-19T17:49:11.624Z Has data issue: false hasContentIssue false
  • English
  • Français

The inertial subrange in turbulent pipe flow: centreline

Published online by Cambridge University Press:  11 January 2016

J. F. Morrison ,
M. Vallikivi  and
A. J. Smits
J. F. Morrison*
Affiliation:
Department of Aeronautics, Imperial College, London SW7 2AZ, UK
M. Vallikivi
Affiliation:
Department of Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ 08544, USA
A. J. Smits
Affiliation:
Department of Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ 08544, USA Department of Mechanical and Aerospace Engineering, Monash University, VIC 3800, Australia
*
†Email address for correspondence: j.morrison@imperial.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

The inertial-subrange scaling of the axial velocity component is examined for the centreline of turbulent pipe flow for Reynolds numbers in the range 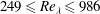$249\leqslant Re_{{\it\lambda}}\leqslant 986$. Estimates of the dissipation rate are made by both integration of the one-dimensional dissipation spectrum and the third-order moment of the structure function. In neither case does the non-dimensional dissipation rate asymptote to a constant; rather than decreasing, it increases indefinitely with Reynolds number. Complete similarity of the inertial range spectra is not evident: there is little support for the hypotheses of Kolmogorov (Dokl. Akad. Nauk SSSR, vol. 32, 1941a, pp. 16–18; Dokl. Akad. Nauk SSSR, vol. 30, 1941b, pp. 301–305) and the effects of Reynolds number are not well represented by Kolmogorov’s ‘extended similarity hypothesis’ (J. Fluid Mech., vol. 13, 1962, pp. 82–85). The second-order moment of the structure function does not show a constant value, even when compensated by the extended similarity hypothesis. When corrected for the effects of finite Reynolds number, the third-order moments of the structure function accurately support the ‘four-fifths law’, but they do not show a clear plateau. In common with recent work in grid turbulence, non-equilibrium effects can be represented by a heuristic scaling that includes a global Reynolds number as well as a local one. It is likely that non-equilibrium effects appear to be particular to the nature of the boundary conditions. Here, the principal effects of the boundary conditions appear through finite turbulent transport at the pipe centreline, which constitutes a source or a sink at each wavenumber.

JFM classification

Turbulent Flows: Isotropic turbulence Boundary Layers: Pipe flow boundary layer Turbulent Flows: Turbulence theory
Type
Papers
Information
Journal of Fluid Mechanics , Volume 788 , 10 February 2016 , pp. 602 - 613
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Antonia, R. A. & Burattini, P. 2006 Approach to the 4/5 law in homogeneous isotropic turbulence. J. Fluid Mech. 550, 175–184.CrossRefGoogle Scholar
Antonia, R. A., Zhou, T. & Romano, G. P. 1997 Second- and third-order longitudinal velocity structure functions in fully developed turbulent channel flow. Phys. Fluids 9, 3465–3471.Google Scholar
Batchelor, G. K. & Townsend, A. A. 1949 The nature of turbulent motion at large wave-numbers. Proc. R. Soc. Lond. A 199, 238–255.Google Scholar
Bradshaw, P.1967 Conditions for the Existence of an Inertial Subrange in Turbulent Flow. Aero. 1220, National Physical Laboratory.Google Scholar
Danaila, L., Anselmat, F., Zhou, T. & Antonia, R. A. 2001 Turbulent energy scale budget equations in a fully developed channel flow. J. Fluid Mech. 430, 87–109.Google Scholar
Davidson, P. A. 2004 Turbulence. An Introduction for Scientists and Engineers. Oxford University Press.Google Scholar
Durbin, P. & Speziale, C. G. 1991 Local anisotropy in strained turbulence at high Reynolds numbers. J. Fluids Engng. 113, 707–709.Google Scholar
Falkovich, G. 1994 Bottleneck phenomenon in developed turbulence. Phys. Fluids 6, 1411–1414.Google Scholar
Frisch, U. 1995 Turbulence: The Legacy of A. N. Kolmogorov. Cambridge University Press.Google Scholar
Grant, H. L., Stewart, R. W. & Moillet, A. 1962 Turbulence spectra from a tidal channel. J. Fluid Mech. 12, 241–268.CrossRefGoogle Scholar
Hultmark, M., Vallikivi, M., Bailey, S. C. C. & Smits, A. J. 2012 Turbulent pipe flow at extreme Reynolds numbers. Phys. Rev. Lett. 108 (9), 1–5.Google Scholar
Hultmark, M., Vallikivi, M., Bailey, S. C. C. & Smits, A. J. 2013 Logarithmic scaling of turbulence in smooth- and rough-wall pipe flow. J. Fluid Mech. 728, 376–395.Google Scholar
Ishihara, T., Gotoh, T. & Kaneda, Y. 2009 Study of high-Reynolds number isotropic turbulence by direct numerical simulation. Annu. Rev. Fluid Mech. 41, 165–180.Google Scholar
Kolmogorov, A. N. 1941a Dissipation of energy in the locally isotropic turbulence. Dokl. Akad. Nauk SSSR 32, 16–18 (translation in Proc. R. Soc. Lond. A 434 15–17).Google Scholar
Kolmogorov, A. N. 1941b The local structure of turbulence in incompressible viscous fluid with very large Reynolds numbers. Dokl. Akad. Nauk SSSR 30, 301–305 (translation in Proc. R. Soc. Lond. A 434 9–13).Google Scholar
Kolmogorov, A. N. 1962 A refinement of previous hypotheses concerning the local structure of turbulence in a viscous incompressible fluid at high Reynolds number. J. Fluid Mech. 13, 82–85.CrossRefGoogle Scholar
Kraichnan, R. H. 1974 On Kolmogorov’s inertial-range theories. J. Fluid Mech. 62, 305–330.Google Scholar
Lumley, J. L. 1967 The inertial subrange in nonequilibrium turbulence. In Atmospheric Turbulence and Radio Wave Propagation (ed. Yaglom, A. M. & Tatarski, V. I.), pp. 157–165. Nauka.Google Scholar
Lumley, J. L. 1992 Some comments on turbulence. Phys. Fluids A 4, 203–211.CrossRefGoogle Scholar
Lundgren, T. S. 2002 Kolmogorov two-thirds law by matched asymptotic expansion. Phys. Fluids 14, 638–642.Google Scholar
Marati, N., Casciola, C. M. & Piva, R. 2004 Energy casacade and spatial fluxes in wall turbulence. J. Fluid Mech. 521, 191–215.Google Scholar
McKeon, B. J. & Morrison, J. F. 2007 Asymptotic scaling in turbulent pipe flow. Phil. Trans. R. Soc. Lond. A 365, 771–787.Google Scholar
Mestayer, P. G. 1982 Local isotropy and anisotropy in a high-Reynolds-number turbulent boundary layer. J. Fluid Mech. 125, 475–503.Google Scholar
Monin, A. S. & Yaglom, A. M. 1975 Statistical Fluid Mechanics: Mechanics of Turbulence. vol. II. MIT Press.Google Scholar
Mydlarski, L. & Warhaft, Z. 1996 On the onset of high-Reynolds-number grid-generated wind tunnel turbulence. J. Fluid Mech. 320, 331–368.Google Scholar
Obukhov, A. M. 1962 Some specific features of atmospheric turbulence. J. Fluid Mech. 13, 77–81.Google Scholar
Rosenberg, B. J., Hultmark, M., Vallikivi, M. & Smits, A. J. 2013 Turbulence spectra in smooth- and rough-wall pipe flow at extreme Reynolds numbers. J. Fluid Mech. 731, 46–63.Google Scholar
Saddoughi, S. G. & Veeravalli, S. V. 1994 Local isotropy in turbulent boundary layers at high Reynolds number. J. Fluid Mech. 268, 333–372.Google Scholar
Sreenivasan, K. R. 1991 On local isotropy of passive scalars in turbulent shear flows. Proc. R. Soc. Lond. A 434, 165–182.Google Scholar
Sreenivasan, K. R. 1995 On the universality of the Kolmogorov constant. Phys. Fluids 7, 2778–2784.CrossRefGoogle Scholar
Sreenivasan, K. R. & Antonia, R. A. 1997 The phenomenology of small-scale turbulence. Annu. Rev. Fluid Mech. 29, 435–472.Google Scholar
Taylor, G. I. 1935 Statistical theory of turbulence. Part I. Proc. R. Soc. Lond. A 151, 421–444.CrossRefGoogle Scholar
Vallikivi, M.2014. Wall-bounded turbulence at high Reynolds numbers. PhD thesis, Princeton University.Google Scholar
Vallikivi, M., Ganapathisubramani, B. & Smits, A. J. 2015 Spectral scaling in boundary layers and pipes at very high Reynolds numbers. J. Fluid Mech. 771, 303–326.Google Scholar
Vallikivi, M., Hultmark, M., Bailey, S. C. C. & Smits, A. J. 2011 Turbulence measurements in pipe flow using a nano-scale thermal anemometry probe. Exp. Fluids 51, 1521–1527.Google Scholar
Vassilicos, J. C. 2015 Dissipation in turbulent flows. Annu. Rev. Fluid Mech. 47, 95–114.Google Scholar