Article contents
Inertial rise of a meniscus on a vertical cylinder
Published online by Cambridge University Press: 03 March 2015
Abstract
We consider the inertia-dominated rise of a meniscus around a vertical circular cylinder. Previous experiments and scaling analysis suggest that the height of the meniscus, 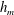 $h_{m}$, grows with the time following the initiation of rise,
$h_{m}$, grows with the time following the initiation of rise,  $t$, like
$t$, like 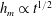 $h_{m}\propto t^{1/2}$. This is in contrast to the rise on a vertical plate, which obeys the classic capillary–inertia scaling
$h_{m}\propto t^{1/2}$. This is in contrast to the rise on a vertical plate, which obeys the classic capillary–inertia scaling 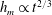 $h_{m}\propto t^{2/3}$. We highlight a subtlety in the scaling analysis that yielded
$h_{m}\propto t^{2/3}$. We highlight a subtlety in the scaling analysis that yielded 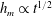 $h_{m}\propto t^{1/2}$ and investigate the consequences of this subtlety. We develop a potential flow model of the dynamic problem, which we solve using the finite element method. Our numerical results agree well with previous experiments but suggest that the correct early time behaviour is, in fact,
$h_{m}\propto t^{1/2}$ and investigate the consequences of this subtlety. We develop a potential flow model of the dynamic problem, which we solve using the finite element method. Our numerical results agree well with previous experiments but suggest that the correct early time behaviour is, in fact, 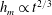 $h_{m}\propto t^{2/3}$. Furthermore, we show that at intermediate times the dynamic rise of the meniscus is governed by two parameters: the contact angle and the cylinder radius measured relative to the capillary length scale,
$h_{m}\propto t^{2/3}$. Furthermore, we show that at intermediate times the dynamic rise of the meniscus is governed by two parameters: the contact angle and the cylinder radius measured relative to the capillary length scale, 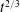 $t^{2/3}$. This result allows us to collapse previous experimental results with different cylinder radii (but similar static contact angles) onto a single master curve.
$t^{2/3}$. This result allows us to collapse previous experimental results with different cylinder radii (but similar static contact angles) onto a single master curve.
- Type
- Rapids
- Information
- Copyright
- © 2015 Cambridge University Press
References
- 4
- Cited by



