Article contents
Inertial gravity currents produced by fluid drainage from an edge
Published online by Cambridge University Press: 29 August 2017
Abstract
We present theoretical, numerical and experimental studies of the release of a finite volume of fluid instantaneously from an edge of a rectangular domain for high Reynolds number flows. For the cases we considered, the results indicate that approximately half of the initial volume exits during an early adjustment period. Then, the inertial gravity current reaches a self-similar phase during which approximately 40 % of its volume drains and its height decreases as 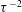 $\unicode[STIX]{x1D70F}^{-2}$, where
$\unicode[STIX]{x1D70F}^{-2}$, where  $\unicode[STIX]{x1D70F}$ is a dimensionless time that is derived with the typical gravity wave speed and the horizontal length of the domain. Based on scaling arguments, we reduce the shallow-water partial differential equations into two nonlinear ordinary differential equations (representing the continuity and momentum equations), which are solved analytically by imposing a zero velocity boundary condition at the closed end wall and a critical Froude number condition at the open edge. The solutions are in good agreement with the performed experiments and direct numerical simulations for various geometries, densities and viscosities. This study provides new insights into the dynamical behaviour of a fluid draining from an edge in the inertial regime. The solutions may be useful for environmental, geophysical and engineering applications such as open channel flows, ventilations and dam-break problems.
$\unicode[STIX]{x1D70F}$ is a dimensionless time that is derived with the typical gravity wave speed and the horizontal length of the domain. Based on scaling arguments, we reduce the shallow-water partial differential equations into two nonlinear ordinary differential equations (representing the continuity and momentum equations), which are solved analytically by imposing a zero velocity boundary condition at the closed end wall and a critical Froude number condition at the open edge. The solutions are in good agreement with the performed experiments and direct numerical simulations for various geometries, densities and viscosities. This study provides new insights into the dynamical behaviour of a fluid draining from an edge in the inertial regime. The solutions may be useful for environmental, geophysical and engineering applications such as open channel flows, ventilations and dam-break problems.
- Type
- Papers
- Information
- Copyright
- © 2017 Cambridge University Press
References
- 13
- Cited by



