Article contents
Inclined porous medium convection at large Rayleigh number
Published online by Cambridge University Press: 05 January 2018
Abstract
High-Rayleigh-number (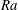 $Ra$) convection in an inclined two-dimensional porous layer is investigated using direct numerical simulations (DNS) and stability and variational upper-bound analyses. When the inclination angle
$Ra$) convection in an inclined two-dimensional porous layer is investigated using direct numerical simulations (DNS) and stability and variational upper-bound analyses. When the inclination angle 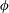 $\unicode[STIX]{x1D719}$ of the layer satisfies
$\unicode[STIX]{x1D719}$ of the layer satisfies  $0^{\circ }<\unicode[STIX]{x1D719}\lesssim 25^{\circ }$, DNS confirm that the flow exhibits a three-region wall-normal asymptotic structure in accord with the strictly horizontal (
$0^{\circ }<\unicode[STIX]{x1D719}\lesssim 25^{\circ }$, DNS confirm that the flow exhibits a three-region wall-normal asymptotic structure in accord with the strictly horizontal (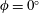 $\unicode[STIX]{x1D719}=0^{\circ }$) case, except that as
$\unicode[STIX]{x1D719}=0^{\circ }$) case, except that as 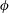 $\unicode[STIX]{x1D719}$ is increased the time-mean spacing between neighbouring interior plumes also increases substantially. Both DNS and upper-bound analysis indicate that the heat transport enhancement factor (i.e. the Nusselt number)
$\unicode[STIX]{x1D719}$ is increased the time-mean spacing between neighbouring interior plumes also increases substantially. Both DNS and upper-bound analysis indicate that the heat transport enhancement factor (i.e. the Nusselt number) 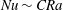 $Nu\sim CRa$ with a
$Nu\sim CRa$ with a 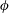 $\unicode[STIX]{x1D719}$-dependent prefactor
$\unicode[STIX]{x1D719}$-dependent prefactor 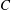 $C$. When
$C$. When 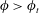 $\unicode[STIX]{x1D719}>\unicode[STIX]{x1D719}_{t}$, however, where
$\unicode[STIX]{x1D719}>\unicode[STIX]{x1D719}_{t}$, however, where  $30^{\circ }<\unicode[STIX]{x1D719}_{t}<32^{\circ }$ independently of
$30^{\circ }<\unicode[STIX]{x1D719}_{t}<32^{\circ }$ independently of 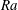 $Ra$, the columnar flow structure is completely broken down: the flow transitions to a large-scale travelling-wave convective roll state, and the heat transport is significantly reduced. To better understand the physics of inclined porous medium convection at large
$Ra$, the columnar flow structure is completely broken down: the flow transitions to a large-scale travelling-wave convective roll state, and the heat transport is significantly reduced. To better understand the physics of inclined porous medium convection at large 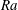 $Ra$ and modest inclination angles, a spatial Floquet analysis is performed, yielding predictions of the linear stability of numerically computed, fully nonlinear steady convective states. The results show that there exist two types of instability when
$Ra$ and modest inclination angles, a spatial Floquet analysis is performed, yielding predictions of the linear stability of numerically computed, fully nonlinear steady convective states. The results show that there exist two types of instability when 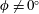 $\unicode[STIX]{x1D719}\neq 0^{\circ }$: a bulk-mode instability and a wall-mode instability, consistent with previous findings for
$\unicode[STIX]{x1D719}\neq 0^{\circ }$: a bulk-mode instability and a wall-mode instability, consistent with previous findings for 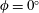 $\unicode[STIX]{x1D719}=0^{\circ }$ (Wen et al., J. Fluid Mech., vol. 772, 2015, pp. 197–224). The background flow induced by the inclination of the layer intensifies the bulk-mode instability during its subsequent nonlinear evolution, thereby favouring increased spacing between the interior plumes relative to that observed in convection in a horizontal porous layer.
$\unicode[STIX]{x1D719}=0^{\circ }$ (Wen et al., J. Fluid Mech., vol. 772, 2015, pp. 197–224). The background flow induced by the inclination of the layer intensifies the bulk-mode instability during its subsequent nonlinear evolution, thereby favouring increased spacing between the interior plumes relative to that observed in convection in a horizontal porous layer.
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
References
- 22
- Cited by


