Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Benzaouia, Mohammed
Tokić, Grgur
Miller, Owen D.
Yue, Dick K.P.
and
Johnson, Steven G.
2019.
From Solar Cells to Ocean Buoys: Wide-Bandwidth Limits to Absorption by Metaparticle Arrays.
Physical Review Applied,
Vol. 11,
Issue. 3,
Tokić, Grgur
and
Yue, Dick K.P.
2021.
Hydrodynamics of large wave energy converter arrays with random configuration variations.
Journal of Fluid Mechanics,
Vol. 923,
Issue. ,
Zhao, Xuanlie
Zhang, Yang
Li, Mingwei
and
Johanning, Lars
2021.
Experimental and analytical investigation on hydrodynamic performance of the comb-type breakwater-wave energy converter system with a flange.
Renewable Energy,
Vol. 172,
Issue. ,
p.
392.
Zhang, Yang
Zhao, Xuanlie
Geng, Jing
Göteman, Malin
and
Tao, Longbin
2022.
Wave power extraction and coastal protection by a periodic array of oscillating buoys embedded in a breakwater.
Renewable Energy,
Vol. 190,
Issue. ,
p.
434.
Göteman, Malin
2022.
Multiple cluster scattering with applications to wave energy park optimizations.
Applied Ocean Research,
Vol. 125,
Issue. ,
p.
103256.
Zeng, Xiaohui
Wang, Qi
Shi, Min
Kang, Yuanshun
and
Yu, Fajun
2022.
Hydrodynamic interactions between waves and cylinder arrays of relative motions composed of truncated floating cylinders with five degrees of freedom.
Journal of Fluids and Structures,
Vol. 115,
Issue. ,
p.
103785.
Gallutia, Daniel
Tahmasbi Fard, Majid
Gutierrez Soto, Mariantonieta
and
He, JiangBiao
2022.
Recent advances in wave energy conversion systems: From wave theory to devices and control strategies.
Ocean Engineering,
Vol. 252,
Issue. ,
p.
111105.
Jin, Huaqing
Zhang, Haicheng
and
Xu, Daolin
2022.
Array buoys with nonlinear stiffness enhance low-frequency wave attenuation and energy capture.
Physics of Fluids,
Vol. 34,
Issue. 12,
Zeng, Xiaohui
Wang, Qi
Kang, Yuanshun
and
Yu, Fajun
2022.
A Novel Type of Wave Energy Converter with Five Degrees of Freedom and Preliminary Investigations on Power-Generating Capacity.
Energies,
Vol. 15,
Issue. 9,
p.
3069.
Zeng, Xiaohui
Wang, Qi
Kang, Yuanshun
and
Yu, Fajun
2022.
Hydrodynamic interactions among wave energy converter array and a hierarchical genetic algorithm for layout optimization.
Ocean Engineering,
Vol. 256,
Issue. ,
p.
111521.
Tokić, Grgur
and
Yue, Dick K. P.
2023.
Axisymmetric reflectors in wave energy converter arrays: Harnessing scattering to increase energy extraction.
Physics of Fluids,
Vol. 35,
Issue. 6,
Zeng, Jinyao
Zhao, Xinyu
Sun, Xiaodong
and
Hu, Xinhua
2023.
Achieving Complete Band Gaps of Water Waves with Shallow-Draft Cylinder Arrays.
Physical Review Applied,
Vol. 19,
Issue. 4,
Zhang, Yang
Zhu, Wenjin
and
Cheng, Xiaofei
2023.
Wave power extraction of flap-type wave energy converter array mounted at the stepped bottom topography.
Renewable Energy,
Vol. 218,
Issue. ,
p.
119334.
Tokić, Grgur
and
Yue, Dick K. P.
2024.
Equilibrium configurations of line arrays with respect to the deviatoric mean drift forces.
Physics of Fluids,
Vol. 36,
Issue. 5,
Zhao, Xuanlie
Zhou, Jiachun
Wang, Zhijie
Zou, Qingping
and
Renzi, Emiliano
2024.
Hydrodynamic performance of multi-chamber oscillating water columns in a caisson array.
Energy,
Vol. 305,
Issue. ,
p.
132217.
Kang, Yuanshun
Zeng, Xiaohui
Cui, Zhehua
and
Chen, Jiahao
2024.
Hydrodynamic responses and layout optimization of wave energy converter arrays consisting of five-degree-of-freedom truncated cylinders in front of a vertical wall.
Physics of Fluids,
Vol. 36,
Issue. 1,
Zhang, Yang
Li, Yuanjie
Zhu, Wenjin
Xu, Qing
Dong, Xiaotian
and
Meng, Yujie
2024.
Hydrodynamic performance of a periodic array of flap-type devices installed on the stepped bottom topography in the front of the coastal wall.
Physics of Fluids,
Vol. 36,
Issue. 2,
Zhu, Kai
Shi, Hongda
Tao, Ji
Gong, Haoxiang
Han, Zhi
and
Cao, Feifei
2024.
Analytical study on hydrodynamic performance of co-located offshore wind–solar farms.
Physics of Fluids,
Vol. 36,
Issue. 1,
Jin, Huaqing
Zhang, Haicheng
Zheng, Siming
and
Xu, Daolin
2024.
Characteristics of a two-dimensional periodic wave energy converter array.
Renewable Energy,
Vol. 222,
Issue. ,
p.
119834.
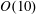 $O(10)$ compared to the same WECs operating in isolation. We show that prominent decreases in array gain are associated with Laue resonances, involving the incident and scattered wave modes, for which we obtain an explicit condition. We also show theoretically that Bragg resonances can result in large decreases in gain with as few as two rows of strong absorbers. For general WEC geometries, we develop a multiple-scattering method of wave–body interactions applicable to generally spaced periodic arrays. For arrays of truncated vertical cylinders, we perform numerical investigations confirming our theoretical predictions for Laue and Bragg resonances. For a special class of multiple-row rectangular WEC arrays, our numerical results show that motion-trapped Rayleigh–Bloch waves can exist and be excited by an incident wave, resulting in sharp, narrow-banded spikes in the array gain.
$O(10)$ compared to the same WECs operating in isolation. We show that prominent decreases in array gain are associated with Laue resonances, involving the incident and scattered wave modes, for which we obtain an explicit condition. We also show theoretically that Bragg resonances can result in large decreases in gain with as few as two rows of strong absorbers. For general WEC geometries, we develop a multiple-scattering method of wave–body interactions applicable to generally spaced periodic arrays. For arrays of truncated vertical cylinders, we perform numerical investigations confirming our theoretical predictions for Laue and Bragg resonances. For a special class of multiple-row rectangular WEC arrays, our numerical results show that motion-trapped Rayleigh–Bloch waves can exist and be excited by an incident wave, resulting in sharp, narrow-banded spikes in the array gain.

