Hostname: page-component-848d4c4894-4rdrl Total loading time: 0 Render date: 2024-06-23T11:57:18.607Z Has data issue: false hasContentIssue false
  • English
  • Français

The hydrodynamic lift of a slender, neutrally buoyant fibre in a wall-bounded shear flow at small Reynolds number

Published online by Cambridge University Press:  19 September 2019

Johnson Dhanasekaran Open the ORCID record for Johnson Dhanasekaran [Opens in a new window]  and
Donald L. Koch Open the ORCID record for Donald L. Koch [Opens in a new window]
Johnson Dhanasekaran
Affiliation:
Sibley School of Mechanical and Aerospace Engineering, Cornell University, Ithaca, NY 14853, USA
Donald L. Koch*
Affiliation:
Robert Frederick Smith School of Chemical and Biomolecular Engineering, Cornell University, Ithaca, NY 14853, USA
*
†Email address for correspondence: dlk15@cornell.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

The hydrodynamic lift velocity of a neutrally buoyant fibre in a simple shear flow near a wall is determined for small, but non-zero, fibre Reynolds number, illustrating the role of non-sphericity in lift. The rotational motion and effects of fibre orientation on lift are treated for fibre positions that induce and do not induce solid-body wall contacts. When the fibre does not contact the wall its lift velocity can be obtained in terms of the Stokes flow field by using a generalized reciprocal theorem. The Stokes velocity field is determined using slender-body theory with the no-slip velocity at the wall enforced using the method of images. To leading order the lift velocity at distances large compared with the fibre length and small compared with the Oseen length is found to be 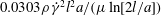$0.0303\unicode[STIX]{x1D70C}\dot{\unicode[STIX]{x1D6FE}}^{2}l^{2}a/(\unicode[STIX]{x1D707}\ln [2l/a])$, where 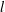$l$ and $a$ are the fibre half-length and radius, 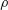$\unicode[STIX]{x1D70C}$ is the density, 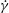$\dot{\unicode[STIX]{x1D6FE}}$ is the shear rate and 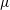$\unicode[STIX]{x1D707}$ is the viscosity of the fluid. When the fibre is close enough to the wall to make solid-body contact during its rotational motion, a process known as pole vaulting coupled with inertially induced changes of fibre orientation determines the lift velocity. The order of magnitude of the lift in this case is larger by a factor of 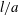$l/a$ than when the fibre does not contact the wall and it reaches a maximum of 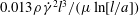$0.013\unicode[STIX]{x1D70C}\dot{\unicode[STIX]{x1D6FE}}^{2}l^{3}/(\unicode[STIX]{x1D707}\ln [l/a])$ for the case of a highly frictional contact and about half that value for a frictionless contact. These results are used to illustrate how particle shape can contribute to separation methods such as those in microfluidic channels or cross-flow filtration processes.

JFM classification

Low-Reynolds-number flows: Slender-body theory Multiphase and Particle-laden Flows: Particle/fluid flow
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 879 , 25 November 2019 , pp. 121 - 146
Check for updates
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Altena, F. W. & Belfort, G. 1984 Lateral migration of spherical particles in porous flow channels: application to membrane filtration. Chem. Engng Sci. 39 (2), 343–355.10.1016/0009-2509(84)80033-0Google Scholar
Batchelor, G. K. 1970 Slender-body theory for particles of arbitrary cross-section in Stokes flow. J. Fluid Mech. 44 (3), 419–440.10.1017/S002211207000191XGoogle Scholar
Belfort, G., Davis, R. H. & Zydney, A. L. 1994 The behavior of suspensions and macromolecular solutions in crossflow microfiltration. J. Membr. Sci. 96 (1-2), 1–58.10.1016/0376-7388(94)00119-7Google Scholar
Blake, J. R. & Chwang, A. T. 1974 Fundamental singularities of viscous flow. J. Engng Maths 8 (1), 23–29.10.1007/BF02353701Google Scholar
Brenner, H. 1961 The slow motion of a sphere through a viscous fluid towards a plane surface. Chem. Engng Sci. 16 (3), 242–251.10.1016/0009-2509(61)80035-3Google Scholar
Cherukat, P. & McLaughlin, J. B. 1994 The inertial lift on a rigid sphere in a linear shear flow field near a flat wall. J. Fluid Mech. 263, 1–18.10.1017/S0022112094004015Google Scholar
Cox, R. G. & Brenner, H. 1967 The slow motion of a sphere through a viscous fluid towards a plane surfaceii small gap widths, including inertial effects. Chem. Engng Sci. 22 (12), 1753–1777.10.1016/0009-2509(67)80208-2Google Scholar
Dabade, V., Marath, N. K. & Subramanian, G. 2016 The effect of inertia on the orientation dynamics of anisotropic particles in simple shear flow. J. Fluid Mech. 791, 631–703.10.1017/jfm.2016.14Google Scholar
Di Carlo, D., Edd, J. F., Irimia, D., Tompkins, R. G. & Toner, M. 2008 Equilibrium separation and filtration of particles using differential inertial focusing. Analyt. Chem. 80 (6), 2204–2211.10.1021/ac702283mGoogle Scholar
Drew, D. A. 1988 The lift force on a small sphere in the presence of a wall. Chem. Engng Sci. 43 (4), 769–773.10.1016/0009-2509(88)80071-XGoogle Scholar
Drew, D. A., Schonberg, J. A. & Belfort, G. 1991 Lateral inertial migration of a small sphere in fast laminar flow through a membrane duct. Chem. Engng Sci. 46 (12), 3219–3224.10.1016/0009-2509(91)85023-QGoogle Scholar
Einarsson, J., Candelier, F., Lundell, F., Angilella, J. R. & Mehlig, B. 2015a Effect of weak fluid inertia upon Jeffery orbits. Phys. Rev. E 91 (4), 041002.Google Scholar
Einarsson, J., Candelier, F., Lundell, F., Angilella, J. R. & Mehlig, B. 2015b Rotation of a spheroid in a simple shear at small Reynolds number. Phys. Fluids 27 (6), 063301.10.1063/1.4921543Google Scholar
Feng, J., Hu, H. H. & Joseph, D. D. 1994 Direct simulation of initial value problems for the motion of solid bodies in a Newtonian fluid. Part 2. Couette and Poiseuille flows. J. Fluid Mech. 277, 271–301.10.1017/S0022112094002764Google Scholar
Harlen, O. G., Sundararajakumar, R. R. & Koch, D. L. 1999 Numerical simulations of a sphere settling through a suspension of neutrally buoyant fibres. J. Fluid Mech. 388, 355–388.10.1017/S0022112099004929Google Scholar
Harper, E. Y. & Chang, I.-D. 1968 Maximum dissipation resulting from lift in a slow viscous shear flow. J. Fluid Mech. 33 (2), 209–225.10.1017/S0022112068001254Google Scholar
Hood, K., Lee, S. & Roper, M. 2015 Inertial migration of a rigid sphere in three-dimensional Poiseuille flow. J. Fluid Mech. 765, 452–479.10.1017/jfm.2014.739Google Scholar
Hurwitz, M. F. & Brantley, J. D. 2000 Shear separation: a promising method for protein fractionation. Le Lait 80 (1), 121–127.10.1051/lait:2000113Google Scholar
Jayageeth, C., Sharma, V. I. & Singh, A. 2009 Dynamics of short fiber suspensions in bounded shear flow. Intl J. Multiphase Flow 35 (3), 261–269.10.1016/j.ijmultiphaseflow.2008.11.002Google Scholar
Jeffery, G. B. 1922 The motion of ellipsoidal particles immersed in a viscous fluid. Proc. R. Soc. Lond. A 102, 161–179.Google Scholar
Khayat, R. E. & Cox, R. G. 1989 Inertia effects on the motion of long slender bodies. J. Fluid Mech. 209, 435–462.10.1017/S0022112089003174Google Scholar
Ku, X. & Lin, J. 2009 Effect of two bounding walls on the rotational motion of a fiber in the simple shear flow. Fibers and Polymers 10 (3), 302–309.10.1007/s12221-009-0302-7Google Scholar
Levesley, J. A. & Bellhouse, B. J. 1993 Particulate separation using inertial lift forces. Chem. Engng Sci. 48 (21), 3657–3669.10.1016/0009-2509(93)81022-NGoogle Scholar
Lovalenti, P. M. & Brady, J. F. 1993 The hydrodynamic force on a rigid particle undergoing arbitrary time-dependent motion at small Reynolds number. J. Fluid Mech. 256, 561–605.10.1017/S0022112093002885Google Scholar
Marath, N. K. & Subramanian, G. 2017 The effect of inertia on the time period of rotation of an anisotropic particle in simple shear flow. J. Fluid Mech. 830, 165–210.10.1017/jfm.2017.534Google Scholar
Masaeli, M., Sollier, E., Amini, H., Mao, W., Camacho, K., Doshi, N., Mitragotri, S., Alexeev, A. & Di Carlo, D. 2012 Continuous inertial focusing and separation of particles by shape. Phys. Rev. X 2 (3), 031017.Google Scholar
McLaughlin, J. B. 1991 Inertial migration of a small sphere in linear shear flows. J. Fluid Mech. 224, 261–274.10.1017/S0022112091001751Google Scholar
McLaughlin, J. B. 1993 The lift on a small sphere in wall-bounded linear shear flows. J. Fluid Mech. 246, 249–265.10.1017/S0022112093000114Google Scholar
Moses, K. B., Advani, S. G. & Reinhardt, A. 2001 Investigation of fiber motion near solid boundaries in simple shear flow. Rheol. Acta 40 (3), 296–306.10.1007/s003970000135Google Scholar
Nagel, M., Brun, P.-T., Berthet, H., Lindner, A., Gallaire, F. & Duprat, C. 2018 Oscillations of confined fibres transported in microchannels. J. Fluid Mech. 835, 444–470.10.1017/jfm.2017.662Google Scholar
Qi, D. 1999 Lattice-Boltzmann simulations of particles in non-zero-Reynolds-number flows. J. Fluid Mech. 385, 41–62.10.1017/S0022112099004401Google Scholar
Rosén, T., Lundell, F. & Aidun, C. K. 2014 Effect of fluid inertia on the dynamics and scaling of neutrally buoyant particles in shear flow. J. Fluid Mech. 738, 563–590.10.1017/jfm.2013.599Google Scholar
Saffman, P. G. T. 1965 The lift on a small sphere in a slow shear flow. J. Fluid Mech. 22 (02), 385–400.10.1017/S0022112065000824Google Scholar
Scheuer, A., Abisset-Chavanne, E., Chinesta, F. & Keunings, R. 2016 Second-gradient modelling of orientation development and rheology of dilute confined suspensions. J. Non-Newtonian Fluid Mech. 237, 54–64.10.1016/j.jnnfm.2016.10.004Google Scholar
Shin, M., Koch, D. L. & Subramanian, G. 2009 Structure and dynamics of dilute suspensions of finite-Reynolds-number settling fibers. Phys. Fluids 21 (12), 123304.10.1063/1.3274612Google Scholar
Stover, C. A. & Cohen, C. 1990 The motion of rodlike particles in the pressure-driven flow between two flat plates. Rheol. Acta 29 (3), 192–203.10.1007/BF01331355Google Scholar
Strednak, S., Shaikh, S., Butler, J. E. & Guazzelli, É. 2018 Shear-induced migration and orientation of rigid fibers in an oscillatory pipe flow. Phys. Rev. Fluids 3 (9), 091301.10.1103/PhysRevFluids.3.091301Google Scholar
Subramanian, G. & Koch, D. L. 2005 Inertial effects on fibre motion in simple shear flow. J. Fluid Mech. 535, 383–414.10.1017/S0022112005004829Google Scholar
Subramony, S.2017 Employing shear induced hydrodynamic lift to achieve sieve-free separation based on size in cross-flow filtration. MS thesis, Cornell University.Google Scholar
Van Dinther, A. M. C., Schroën, C. G. P. H., Imhof, A., Vollebregt, H. M. & Boom, R. M. 2013 Flow-induced particle migration in microchannels for improved microfiltration processes. Microfluid. Nanofluid. 15 (4), 451–465.10.1007/s10404-013-1158-0Google Scholar
Yan, Z.-Y., Acrivos, A. & Weinbaum, S. 1991 Fluid skimming and particle entrainment into a small circular side pore. J. Fluid Mech. 229, 1–27.10.1017/S0022112091002914Google Scholar
Yang, S.-M. & Leal, L. G. 1984 Particle motion in Stokes flow near a plane fluid–fluid interface. Part 2. Linear shear and axisymmetric straining flows. J. Fluid Mech. 149, 275–304.10.1017/S0022112084002652Google Scholar