1 Introduction
The recent work of Kahkeshani, Haddadi & Di Carlo (Reference Kahkeshani, Haddadi and Di Carlo2016), hereafter KHD, shows that particles in a microchannel flow can adopt strikingly regular patterns, with many particles moving at nearly fixed axial separation. Phenomena leading to particle ordering are explored, motivated by the utility of ordering in such applications as cell sorting.
As shown by figure 1 (and in movies provided as supplementary material available at https://doi.org/10.1017/jfm.2016.51), the particles enter the channel randomly and form lines or ‘trains’ (as described by Matas et al.
Reference Matas, Glezer, Morris and Guazzelli2004). This structure results from lateral migration combined with hydrodynamic interactions between particles. Lateral migration within the cross-section can be a consequence of particle deformability or non-Newtonian fluid rheology. However, in KHD, the fluid is Newtonian and the particles are undeformed, leaving only inertia to drive migration. Inertial effects may be surprising for microchannel flows, but the low-viscosity liquid (mostly water) yields channel Reynolds numbers of
 $\mathit{Re}_{c}=O(100)$
.
$\mathit{Re}_{c}=O(100)$
.
Inertial migration was described by Segré & Silberberg (Reference Segré and Silberberg1962), who found focusing to a preferred radius,
 $r^{\ast }$
, in a circular tube. The basis for the preferred radius was presented by Ho & Leal (Reference Ho and Leal1974), while theory based on a point-particle approximation (Schonberg & Hinch Reference Schonberg and Hinch1989) shows that
$r^{\ast }$
, in a circular tube. The basis for the preferred radius was presented by Ho & Leal (Reference Ho and Leal1974), while theory based on a point-particle approximation (Schonberg & Hinch Reference Schonberg and Hinch1989) shows that
 $r^{\ast }$
moves toward the boundary with increasing
$r^{\ast }$
moves toward the boundary with increasing
 $\mathit{Re}_{c}$
.
$\mathit{Re}_{c}$
.
Microfluidic technology has generated interest in non-circular conduits and conditions of strong confinement, for which the particle size is a quite large fraction of the cross-section. In KHD, the particle diameter is fully one-third of the narrow dimension of a rectangular channel. For these conditions, point-particle theories are suspect, and what is known is deduced from experiment and simulation. For example, experiments by Miura, Itano & Sugihara-Seki (Reference Miura, Itano and Sugihara-Seki2014) show migration in a square channel to focusing points which vary with
 $\mathit{Re}_{c}$
, in partial agreement with discrete-particle simulations by Chun & Ladd (Reference Chun and Ladd2006). A combination of experiments and numerical simulation for rectangular geometries in Humphry et al. (Reference Humphry, Kulkarni, Weitz, Morris and Stone2010) was able to capture the evolution to the focusing positions in a rectangular channel, and gave some guidance to the basis for ‘train’ formation. This particle-train formation, and how the particle spacing depends on solid fraction and flow rate, are the subject of KHD.
$\mathit{Re}_{c}$
, in partial agreement with discrete-particle simulations by Chun & Ladd (Reference Chun and Ladd2006). A combination of experiments and numerical simulation for rectangular geometries in Humphry et al. (Reference Humphry, Kulkarni, Weitz, Morris and Stone2010) was able to capture the evolution to the focusing positions in a rectangular channel, and gave some guidance to the basis for ‘train’ formation. This particle-train formation, and how the particle spacing depends on solid fraction and flow rate, are the subject of KHD.
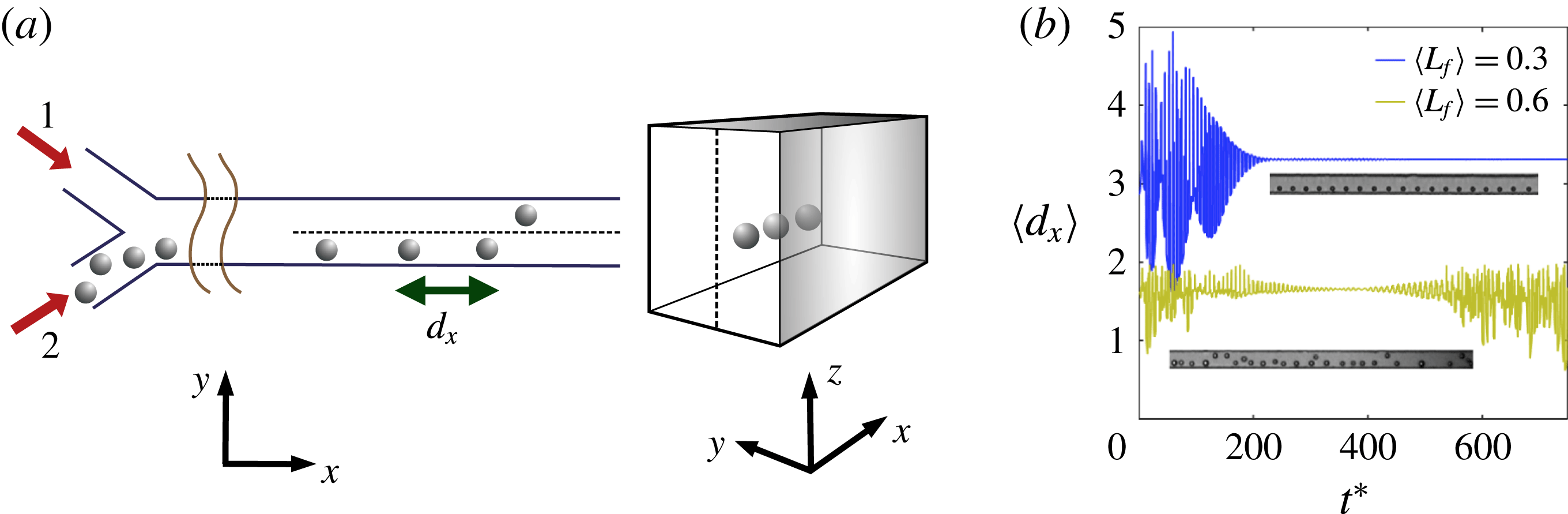
Figure 1. (a) Schematic of the microfluidic channel, showing particle entry only from arm 2 at left, and the form of the ordering into trains at right. (b) Relative separation with time and images of particle ordering for different linear densities at
 $\mathit{Re}_{p}=2.8$
, showing stable ordering at
$\mathit{Re}_{p}=2.8$
, showing stable ordering at
 $\langle L_{f}\rangle =0.3$
and loss of stability at
$\langle L_{f}\rangle =0.3$
and loss of stability at
 $\langle L_{f}\rangle =0.6$
.
$\langle L_{f}\rangle =0.6$
.
2 Overview
In KHD, pressure-driven flow is studied in a rectangular channel with dimensions
 $l_{y}\times l_{z}\times l_{x}=35~\unicode[STIX]{x03BC}\text{m}\times 60~\unicode[STIX]{x03BC}\text{m}\times 3~\text{cm}$
;
$l_{y}\times l_{z}\times l_{x}=35~\unicode[STIX]{x03BC}\text{m}\times 60~\unicode[STIX]{x03BC}\text{m}\times 3~\text{cm}$
;
 $x$
is the flow direction as shown in figure 1(a). The particles have diameter
$x$
is the flow direction as shown in figure 1(a). The particles have diameter
 $D=12~\unicode[STIX]{x03BC}\text{m}$
and are highly confined:
$D=12~\unicode[STIX]{x03BC}\text{m}$
and are highly confined:
 $D/l_{y}\approx 1/3$
. Variations of behaviour can be described in terms of particle volume fraction,
$D/l_{y}\approx 1/3$
. Variations of behaviour can be described in terms of particle volume fraction,
 $\unicode[STIX]{x1D719}$
, and channel Reynolds number,
$\unicode[STIX]{x1D719}$
, and channel Reynolds number,
 $\mathit{Re}_{c}=l_{y}U/\unicode[STIX]{x1D708}$
;
$\mathit{Re}_{c}=l_{y}U/\unicode[STIX]{x1D708}$
;
 $\unicode[STIX]{x1D708}\approx 8\times 10^{-6}~\text{m}^{2}~\text{s}^{-1}$
is the kinematic viscosity of the liquid, and the average axial velocity is
$\unicode[STIX]{x1D708}\approx 8\times 10^{-6}~\text{m}^{2}~\text{s}^{-1}$
is the kinematic viscosity of the liquid, and the average axial velocity is
 $U=0.7$
–2.7 m s
$U=0.7$
–2.7 m s
 $^{-1}$
, yielding
$^{-1}$
, yielding
 $\mathit{Re}_{c}=30$
–120. The authors use particle Reynolds number
$\mathit{Re}_{c}=30$
–120. The authors use particle Reynolds number
 $\mathit{Re}_{p}=(D/l_{y})^{2}\mathit{Re}_{c}$
, which determines the disturbance flow caused by the particles.
$\mathit{Re}_{p}=(D/l_{y})^{2}\mathit{Re}_{c}$
, which determines the disturbance flow caused by the particles.
The ordering observed in KHD results first from the tendency to inertially focus due to lateral migration to preferred positions in the cross-section, and second from hydrodynamic interactions (HIs) between particles. The HIs are influenced by inertia and confinement. At small
 $\unicode[STIX]{x1D719}$
, the particles focus to the mid-plane in the longer dimension of the cross-section (
$\unicode[STIX]{x1D719}$
, the particles focus to the mid-plane in the longer dimension of the cross-section (
 $Z$
), at locations to either side of the centreline in the other dimension (
$Z$
), at locations to either side of the centreline in the other dimension (
 $Y$
). However, as shown in figure 1(a), the particles enter from only one of two arms entering the channel, so that isolation and ordering are mostly into a single line. It is thus convenient to use the length fraction
$Y$
). However, as shown in figure 1(a), the particles enter from only one of two arms entering the channel, so that isolation and ordering are mostly into a single line. It is thus convenient to use the length fraction
 $\langle L_{f}\rangle =\langle N\rangle D/L$
with
$\langle L_{f}\rangle =\langle N\rangle D/L$
with
 $\langle N\rangle$
the average number of particles within the viewing frame of length
$\langle N\rangle$
the average number of particles within the viewing frame of length
 $L$
. For
$L$
. For
 $\langle L_{f}\rangle \approx 0.1$
, the preferred axial spacing undergoes a transition from
$\langle L_{f}\rangle \approx 0.1$
, the preferred axial spacing undergoes a transition from
 $d_{x}/D\approx 5$
at
$d_{x}/D\approx 5$
at
 $\mathit{Re}_{p}=2.8$
to
$\mathit{Re}_{p}=2.8$
to
 $d_{x}\approx 2.5D$
at
$d_{x}\approx 2.5D$
at
 $\mathit{Re}_{p}=8.3$
.
$\mathit{Re}_{p}=8.3$
.
The change in preferred locations was probed using simulations, by the lattice-Boltzmann technique for suspensions (Ladd Reference Ladd1994), of the relative trajectories of particles. While confinement results in flow reversal zones even in Stokes flow (Zurita-Gotor, Blawzdziewicz & Wajnryb Reference Zurita-Gotor, Blawzdziewicz and Wajnryb2007), the adoption of fixed separations regardless of initial condition requires fluid mechanical nonlinearity, i.e.
 $\mathit{Re}_{p}\neq 0$
. In figure 2, the trajectories of particles show that at
$\mathit{Re}_{p}\neq 0$
. In figure 2, the trajectories of particles show that at
 $\mathit{Re}_{p}=2.8$
, particles starting at a range of positions relative to the first (at the focusing position) all approach, reverse and then move to the same separation: once in this location, the particles occupy the same cross-section location and move together axially at a nearly fixed separation of
$\mathit{Re}_{p}=2.8$
, particles starting at a range of positions relative to the first (at the focusing position) all approach, reverse and then move to the same separation: once in this location, the particles occupy the same cross-section location and move together axially at a nearly fixed separation of
 $d_{x}/D\approx 5$
. At
$d_{x}/D\approx 5$
. At
 $\mathit{Re}_{p}=8.3$
, these pair simulations show that particles which start at small
$\mathit{Re}_{p}=8.3$
, these pair simulations show that particles which start at small
 $Z$
adopt
$Z$
adopt
 $d_{x}/D\approx 5$
, whereas those starting at smaller
$d_{x}/D\approx 5$
, whereas those starting at smaller
 $Z$
move to
$Z$
move to
 $2<d_{x}/D<2.5$
; intermediate separations are not found. In a many-body system, the presence of a particle at
$2<d_{x}/D<2.5$
; intermediate separations are not found. In a many-body system, the presence of a particle at
 $d_{x}/D\approx 2.5$
would force a particle which, under isolated-pair conditions, might move to
$d_{x}/D\approx 2.5$
would force a particle which, under isolated-pair conditions, might move to
 $d_{x}/D\approx 5$
(relative to the first) to a position of
$d_{x}/D\approx 5$
(relative to the first) to a position of
 $d_{x}/D\approx 2.5$
relative to the second, and the process is thus able to order the particles at the fixed smaller separation.
$d_{x}/D\approx 2.5$
relative to the second, and the process is thus able to order the particles at the fixed smaller separation.
Figure 2. Computed trajectories of a second particle released at various separations relative to a first at the focusing point for (a)
 $\mathit{Re}_{p}=2.8$
and (b)
$\mathit{Re}_{p}=2.8$
and (b)
 $\mathit{Re}_{p}=8.3$
.
$\mathit{Re}_{p}=8.3$
.
With increase in
 $\langle L_{f}\rangle$
(increase of
$\langle L_{f}\rangle$
(increase of
 $\unicode[STIX]{x1D719}$
) at fixed
$\unicode[STIX]{x1D719}$
) at fixed
 $\mathit{Re}_{p}$
,
$\mathit{Re}_{p}$
,
 $d_{x}/D$
decreases to accommodate the particles at the focusing position as shown in figure 1(b):
$d_{x}/D$
decreases to accommodate the particles at the focusing position as shown in figure 1(b):
 $d_{x}/D\approx 3.2$
for
$d_{x}/D\approx 3.2$
for
 $\langle L_{f}\rangle =0.3$
and
$\langle L_{f}\rangle =0.3$
and
 $\mathit{Re}_{p}=2.8$
, considerably smaller than
$\mathit{Re}_{p}=2.8$
, considerably smaller than
 $d_{x}/D\approx 5$
seen at
$d_{x}/D\approx 5$
seen at
 $\langle L_{f}\rangle =0.1$
. Further increase of the loading to
$\langle L_{f}\rangle =0.1$
. Further increase of the loading to
 $\langle L_{f}\rangle =0.6$
is shown in the same figure to result in a loss of the stable axial order with fluctuating separations.
$\langle L_{f}\rangle =0.6$
is shown in the same figure to result in a loss of the stable axial order with fluctuating separations.
3 Future
Microfluidic platforms provide a ‘laboratory on a chip’ where scientific experimentation can be performed in remarkably small volumes. A range of basic processes, such as microscale separation (Zhou et al.
Reference Zhou, Giridar, Kasper and Papautsky2014) or mixing, can be performed on-chip. For particle-laden flows, this supports examination of reaction chemistry at particle surfaces or cellular interactions with solution components, among many possibilities.
The work of KHD is motivated by applications in medical diagnostics, where microfluidics has the potential to revolutionize cytometry and cell sorting. In cell sorting, regular arrival times of an ordered train facilitate rapid detection and isolation, supporting high throughput screening to find rare cells. The ordering described in KHD does, however, become more difficult when applied to cell populations, where there is size dispersion and deformability. Evidence for the potential of methods which use both inertia and deformability to discriminate cell populations has been provided by Hur et al. (Reference Hur, Henderson-MacLenna, McCabe and Di Carlo2011), but much is left to be done. Another example is to follow the ordering by encapsulation of the particles (or cells) into drops using flow focusing, a standard microfluidic element (Anna, Bontoux & Stone Reference Anna, Bontoux and Stone2003) which brings an immiscible sheath fluid around the main stream to cause drop pinch-off. If controlled to each contain one cell, each drop serves as a picolitre to nanolitre environment for a single cell. If ordered particles and ordered cell streams can be combined to have a single particle and a single cell in a drop, assaying tools can be introduced on the particle to deduce the cellular response.
The work of KHD has developed clear understanding of inertial migration and the particle ordering which follows. While applied to a specific geometry, both in terms of channel and confinement ratio, the approach provides a methodology applicable to general conditions. Ultimately, there is a real need for mechanistic understanding of the phenomena involved in inertial microfluidic systems, such that a computed flow of the fluid alone could be used to predict the cross-sectional location of particles. This is presently lacking, but does not seem far out of reach. Such understanding could be used in a description of the particle dynamics in terms of forces on particles immersed in inertial flows in conduits of arbitrary form. Regardless of the form of the tools developed, fully elaborating the fluid mechanical phenomena involved in particle ordering in microchannels will remove a critical hurdle to rational development of a suite of powerful microfluidic methods.
$\mathit{Re}_{p}=2.8$, showing stable ordering at
$\langle L_{f}\rangle =0.3$ and loss of stability at
$\langle L_{f}\rangle =0.6$.

$\mathit{Re}_{p}=2.8$ and (b)
$\mathit{Re}_{p}=8.3$.




1 Introduction
The recent work of Kahkeshani, Haddadi & Di Carlo (Reference Kahkeshani, Haddadi and Di Carlo2016), hereafter KHD, shows that particles in a microchannel flow can adopt strikingly regular patterns, with many particles moving at nearly fixed axial separation. Phenomena leading to particle ordering are explored, motivated by the utility of ordering in such applications as cell sorting.
As shown by figure 1 (and in movies provided as supplementary material available at https://doi.org/10.1017/jfm.2016.51), the particles enter the channel randomly and form lines or ‘trains’ (as described by Matas et al. Reference Matas, Glezer, Morris and Guazzelli2004). This structure results from lateral migration combined with hydrodynamic interactions between particles. Lateral migration within the cross-section can be a consequence of particle deformability or non-Newtonian fluid rheology. However, in KHD, the fluid is Newtonian and the particles are undeformed, leaving only inertia to drive migration. Inertial effects may be surprising for microchannel flows, but the low-viscosity liquid (mostly water) yields channel Reynolds numbers of $\mathit{Re}_{c}=O(100)$
.
$\mathit{Re}_{c}=O(100)$
.
Inertial migration was described by Segré & Silberberg (Reference Segré and Silberberg1962), who found focusing to a preferred radius, $r^{\ast }$
, in a circular tube. The basis for the preferred radius was presented by Ho & Leal (Reference Ho and Leal1974), while theory based on a point-particle approximation (Schonberg & Hinch Reference Schonberg and Hinch1989) shows that
$r^{\ast }$
, in a circular tube. The basis for the preferred radius was presented by Ho & Leal (Reference Ho and Leal1974), while theory based on a point-particle approximation (Schonberg & Hinch Reference Schonberg and Hinch1989) shows that
 $r^{\ast }$
moves toward the boundary with increasing
$r^{\ast }$
moves toward the boundary with increasing
 $\mathit{Re}_{c}$
.
$\mathit{Re}_{c}$
.
Microfluidic technology has generated interest in non-circular conduits and conditions of strong confinement, for which the particle size is a quite large fraction of the cross-section. In KHD, the particle diameter is fully one-third of the narrow dimension of a rectangular channel. For these conditions, point-particle theories are suspect, and what is known is deduced from experiment and simulation. For example, experiments by Miura, Itano & Sugihara-Seki (Reference Miura, Itano and Sugihara-Seki2014) show migration in a square channel to focusing points which vary with $\mathit{Re}_{c}$
, in partial agreement with discrete-particle simulations by Chun & Ladd (Reference Chun and Ladd2006). A combination of experiments and numerical simulation for rectangular geometries in Humphry et al. (Reference Humphry, Kulkarni, Weitz, Morris and Stone2010) was able to capture the evolution to the focusing positions in a rectangular channel, and gave some guidance to the basis for ‘train’ formation. This particle-train formation, and how the particle spacing depends on solid fraction and flow rate, are the subject of KHD.
$\mathit{Re}_{c}$
, in partial agreement with discrete-particle simulations by Chun & Ladd (Reference Chun and Ladd2006). A combination of experiments and numerical simulation for rectangular geometries in Humphry et al. (Reference Humphry, Kulkarni, Weitz, Morris and Stone2010) was able to capture the evolution to the focusing positions in a rectangular channel, and gave some guidance to the basis for ‘train’ formation. This particle-train formation, and how the particle spacing depends on solid fraction and flow rate, are the subject of KHD.
Figure 1. (a) Schematic of the microfluidic channel, showing particle entry only from arm 2 at left, and the form of the ordering into trains at right. (b) Relative separation with time and images of particle ordering for different linear densities at $\mathit{Re}_{p}=2.8$
, showing stable ordering at
$\mathit{Re}_{p}=2.8$
, showing stable ordering at
 $\langle L_{f}\rangle =0.3$
and loss of stability at
$\langle L_{f}\rangle =0.3$
and loss of stability at
 $\langle L_{f}\rangle =0.6$
.
$\langle L_{f}\rangle =0.6$
.
2 Overview
In KHD, pressure-driven flow is studied in a rectangular channel with dimensions $l_{y}\times l_{z}\times l_{x}=35~\unicode[STIX]{x03BC}\text{m}\times 60~\unicode[STIX]{x03BC}\text{m}\times 3~\text{cm}$
;
$l_{y}\times l_{z}\times l_{x}=35~\unicode[STIX]{x03BC}\text{m}\times 60~\unicode[STIX]{x03BC}\text{m}\times 3~\text{cm}$
;
 $x$
is the flow direction as shown in figure 1(a). The particles have diameter
$x$
is the flow direction as shown in figure 1(a). The particles have diameter
 $D=12~\unicode[STIX]{x03BC}\text{m}$
and are highly confined:
$D=12~\unicode[STIX]{x03BC}\text{m}$
and are highly confined:
 $D/l_{y}\approx 1/3$
. Variations of behaviour can be described in terms of particle volume fraction,
$D/l_{y}\approx 1/3$
. Variations of behaviour can be described in terms of particle volume fraction,
 $\unicode[STIX]{x1D719}$
, and channel Reynolds number,
$\unicode[STIX]{x1D719}$
, and channel Reynolds number,
 $\mathit{Re}_{c}=l_{y}U/\unicode[STIX]{x1D708}$
;
$\mathit{Re}_{c}=l_{y}U/\unicode[STIX]{x1D708}$
;
 $\unicode[STIX]{x1D708}\approx 8\times 10^{-6}~\text{m}^{2}~\text{s}^{-1}$
is the kinematic viscosity of the liquid, and the average axial velocity is
$\unicode[STIX]{x1D708}\approx 8\times 10^{-6}~\text{m}^{2}~\text{s}^{-1}$
is the kinematic viscosity of the liquid, and the average axial velocity is
 $U=0.7$
–2.7 m s
$U=0.7$
–2.7 m s
 $^{-1}$
, yielding
$^{-1}$
, yielding
 $\mathit{Re}_{c}=30$
–120. The authors use particle Reynolds number
$\mathit{Re}_{c}=30$
–120. The authors use particle Reynolds number
 $\mathit{Re}_{p}=(D/l_{y})^{2}\mathit{Re}_{c}$
, which determines the disturbance flow caused by the particles.
$\mathit{Re}_{p}=(D/l_{y})^{2}\mathit{Re}_{c}$
, which determines the disturbance flow caused by the particles.
The ordering observed in KHD results first from the tendency to inertially focus due to lateral migration to preferred positions in the cross-section, and second from hydrodynamic interactions (HIs) between particles. The HIs are influenced by inertia and confinement. At small $\unicode[STIX]{x1D719}$
, the particles focus to the mid-plane in the longer dimension of the cross-section (
$\unicode[STIX]{x1D719}$
, the particles focus to the mid-plane in the longer dimension of the cross-section (
 $Z$
), at locations to either side of the centreline in the other dimension (
$Z$
), at locations to either side of the centreline in the other dimension (
 $Y$
). However, as shown in figure 1(a), the particles enter from only one of two arms entering the channel, so that isolation and ordering are mostly into a single line. It is thus convenient to use the length fraction
$Y$
). However, as shown in figure 1(a), the particles enter from only one of two arms entering the channel, so that isolation and ordering are mostly into a single line. It is thus convenient to use the length fraction
 $\langle L_{f}\rangle =\langle N\rangle D/L$
with
$\langle L_{f}\rangle =\langle N\rangle D/L$
with
 $\langle N\rangle$
the average number of particles within the viewing frame of length
$\langle N\rangle$
the average number of particles within the viewing frame of length
 $L$
. For
$L$
. For
 $\langle L_{f}\rangle \approx 0.1$
, the preferred axial spacing undergoes a transition from
$\langle L_{f}\rangle \approx 0.1$
, the preferred axial spacing undergoes a transition from
 $d_{x}/D\approx 5$
at
$d_{x}/D\approx 5$
at
 $\mathit{Re}_{p}=2.8$
to
$\mathit{Re}_{p}=2.8$
to
 $d_{x}\approx 2.5D$
at
$d_{x}\approx 2.5D$
at
 $\mathit{Re}_{p}=8.3$
.
$\mathit{Re}_{p}=8.3$
.
The change in preferred locations was probed using simulations, by the lattice-Boltzmann technique for suspensions (Ladd Reference Ladd1994), of the relative trajectories of particles. While confinement results in flow reversal zones even in Stokes flow (Zurita-Gotor, Blawzdziewicz & Wajnryb Reference Zurita-Gotor, Blawzdziewicz and Wajnryb2007), the adoption of fixed separations regardless of initial condition requires fluid mechanical nonlinearity, i.e. $\mathit{Re}_{p}\neq 0$
. In figure 2, the trajectories of particles show that at
$\mathit{Re}_{p}\neq 0$
. In figure 2, the trajectories of particles show that at
 $\mathit{Re}_{p}=2.8$
, particles starting at a range of positions relative to the first (at the focusing position) all approach, reverse and then move to the same separation: once in this location, the particles occupy the same cross-section location and move together axially at a nearly fixed separation of
$\mathit{Re}_{p}=2.8$
, particles starting at a range of positions relative to the first (at the focusing position) all approach, reverse and then move to the same separation: once in this location, the particles occupy the same cross-section location and move together axially at a nearly fixed separation of
 $d_{x}/D\approx 5$
. At
$d_{x}/D\approx 5$
. At
 $\mathit{Re}_{p}=8.3$
, these pair simulations show that particles which start at small
$\mathit{Re}_{p}=8.3$
, these pair simulations show that particles which start at small
 $Z$
adopt
$Z$
adopt
 $d_{x}/D\approx 5$
, whereas those starting at smaller
$d_{x}/D\approx 5$
, whereas those starting at smaller
 $Z$
move to
$Z$
move to
 $2<d_{x}/D<2.5$
; intermediate separations are not found. In a many-body system, the presence of a particle at
$2<d_{x}/D<2.5$
; intermediate separations are not found. In a many-body system, the presence of a particle at
 $d_{x}/D\approx 2.5$
would force a particle which, under isolated-pair conditions, might move to
$d_{x}/D\approx 2.5$
would force a particle which, under isolated-pair conditions, might move to
 $d_{x}/D\approx 5$
(relative to the first) to a position of
$d_{x}/D\approx 5$
(relative to the first) to a position of
 $d_{x}/D\approx 2.5$
relative to the second, and the process is thus able to order the particles at the fixed smaller separation.
$d_{x}/D\approx 2.5$
relative to the second, and the process is thus able to order the particles at the fixed smaller separation.
Figure 2. Computed trajectories of a second particle released at various separations relative to a first at the focusing point for (a) $\mathit{Re}_{p}=2.8$
and (b)
$\mathit{Re}_{p}=2.8$
and (b)
 $\mathit{Re}_{p}=8.3$
.
$\mathit{Re}_{p}=8.3$
.
With increase in $\langle L_{f}\rangle$
(increase of
$\langle L_{f}\rangle$
(increase of
 $\unicode[STIX]{x1D719}$
) at fixed
$\unicode[STIX]{x1D719}$
) at fixed
 $\mathit{Re}_{p}$
,
$\mathit{Re}_{p}$
,
 $d_{x}/D$
decreases to accommodate the particles at the focusing position as shown in figure 1(b):
$d_{x}/D$
decreases to accommodate the particles at the focusing position as shown in figure 1(b):
 $d_{x}/D\approx 3.2$
for
$d_{x}/D\approx 3.2$
for
 $\langle L_{f}\rangle =0.3$
and
$\langle L_{f}\rangle =0.3$
and
 $\mathit{Re}_{p}=2.8$
, considerably smaller than
$\mathit{Re}_{p}=2.8$
, considerably smaller than
 $d_{x}/D\approx 5$
seen at
$d_{x}/D\approx 5$
seen at
 $\langle L_{f}\rangle =0.1$
. Further increase of the loading to
$\langle L_{f}\rangle =0.1$
. Further increase of the loading to
 $\langle L_{f}\rangle =0.6$
is shown in the same figure to result in a loss of the stable axial order with fluctuating separations.
$\langle L_{f}\rangle =0.6$
is shown in the same figure to result in a loss of the stable axial order with fluctuating separations.
3 Future
Microfluidic platforms provide a ‘laboratory on a chip’ where scientific experimentation can be performed in remarkably small volumes. A range of basic processes, such as microscale separation (Zhou et al. Reference Zhou, Giridar, Kasper and Papautsky2014) or mixing, can be performed on-chip. For particle-laden flows, this supports examination of reaction chemistry at particle surfaces or cellular interactions with solution components, among many possibilities.
The work of KHD is motivated by applications in medical diagnostics, where microfluidics has the potential to revolutionize cytometry and cell sorting. In cell sorting, regular arrival times of an ordered train facilitate rapid detection and isolation, supporting high throughput screening to find rare cells. The ordering described in KHD does, however, become more difficult when applied to cell populations, where there is size dispersion and deformability. Evidence for the potential of methods which use both inertia and deformability to discriminate cell populations has been provided by Hur et al. (Reference Hur, Henderson-MacLenna, McCabe and Di Carlo2011), but much is left to be done. Another example is to follow the ordering by encapsulation of the particles (or cells) into drops using flow focusing, a standard microfluidic element (Anna, Bontoux & Stone Reference Anna, Bontoux and Stone2003) which brings an immiscible sheath fluid around the main stream to cause drop pinch-off. If controlled to each contain one cell, each drop serves as a picolitre to nanolitre environment for a single cell. If ordered particles and ordered cell streams can be combined to have a single particle and a single cell in a drop, assaying tools can be introduced on the particle to deduce the cellular response.
The work of KHD has developed clear understanding of inertial migration and the particle ordering which follows. While applied to a specific geometry, both in terms of channel and confinement ratio, the approach provides a methodology applicable to general conditions. Ultimately, there is a real need for mechanistic understanding of the phenomena involved in inertial microfluidic systems, such that a computed flow of the fluid alone could be used to predict the cross-sectional location of particles. This is presently lacking, but does not seem far out of reach. Such understanding could be used in a description of the particle dynamics in terms of forces on particles immersed in inertial flows in conduits of arbitrary form. Regardless of the form of the tools developed, fully elaborating the fluid mechanical phenomena involved in particle ordering in microchannels will remove a critical hurdle to rational development of a suite of powerful microfluidic methods.
Supplementary movies
Supplementary movies are available at https://doi.org/10.1017/jfm.2016.51.