Article contents
High-speed granular chute flows
Published online by Cambridge University Press: 31 August 2012
Abstract
This paper reports experimental findings on the flow of sand down a steep chute. Nearly all granular flow models have a maximum value for the friction and therefore predict that flows on steep slopes will accelerate at a constant rate until the interaction with the ambient fluid becomes important. This prediction has not been tested by previous work, which has focused on relatively low slope angles where steady, fully developed flows occur after short distances. We test this by investigating flows over a much greater range of slope angles (30–50 ) and flow depths (4–130 particle diameters). We examine flows with two basal conditions, one flat and frictional, the other bumpy. The latter imposes a no-slip condition for slow, deep flows, but permits some degree of slip for high flow velocities. The data suggests that friction can be much larger than theories such as the
) and flow depths (4–130 particle diameters). We examine flows with two basal conditions, one flat and frictional, the other bumpy. The latter imposes a no-slip condition for slow, deep flows, but permits some degree of slip for high flow velocities. The data suggests that friction can be much larger than theories such as the 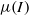 rheology proposed by Jop, Forterre & Pouliquen (Nature, vol. 441, 2006) suggest and that there may be constant velocity states above the angle of vanishing
rheology proposed by Jop, Forterre & Pouliquen (Nature, vol. 441, 2006) suggest and that there may be constant velocity states above the angle of vanishing 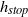 . Although these flows do not vary in time, all but the flows on the bumpy base at low inclinations accelerate down the slope. A recirculation mechanism sustains flows with a maximum mass flux of
. Although these flows do not vary in time, all but the flows on the bumpy base at low inclinations accelerate down the slope. A recirculation mechanism sustains flows with a maximum mass flux of 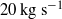 , allowing observations to be made at multiple points for each flow for an indefinite period. Flows with Froude number in the range 0.1–25 and bulk inertial number 0.1–2.7 were observed in the dense regime, with surface velocities in the range 0.2–5.6
, allowing observations to be made at multiple points for each flow for an indefinite period. Flows with Froude number in the range 0.1–25 and bulk inertial number 0.1–2.7 were observed in the dense regime, with surface velocities in the range 0.2–5.6 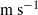 . Previous studies have focused on
. Previous studies have focused on 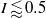 . We show that a numerical implementation of the
. We show that a numerical implementation of the 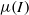 rheology does not fully capture the accelerating dynamics or the transverse velocity profile on the bumpy base. We also observe the transverse separation of the flow into a dense core flanked by dilute regions and the formation of longitudinal vortices.
rheology does not fully capture the accelerating dynamics or the transverse velocity profile on the bumpy base. We also observe the transverse separation of the flow into a dense core flanked by dilute regions and the formation of longitudinal vortices.
JFM classification
- Type
- Papers
- Information
- Copyright
- Copyright © Cambridge University Press 2012
References
- 51
- Cited by


