Published online by Cambridge University Press: 06 June 2022
We report direct numerical simulations (DNS) of the Nusselt number  $Nu$, the vertical profiles of mean temperature
$Nu$, the vertical profiles of mean temperature  $\varTheta (z)$ and temperature variance
$\varTheta (z)$ and temperature variance  $\varOmega (z)$ across the thermal boundary layer (BL) in closed turbulent Rayleigh–Bénard convection (RBC) with slippery conducting surfaces (
$\varOmega (z)$ across the thermal boundary layer (BL) in closed turbulent Rayleigh–Bénard convection (RBC) with slippery conducting surfaces ( $z$ is the vertical distance from the bottom surface). The DNS study was conducted in three RBC samples: a three-dimensional cuboid with length
$z$ is the vertical distance from the bottom surface). The DNS study was conducted in three RBC samples: a three-dimensional cuboid with length  $L = H$ and width
$L = H$ and width  $W = H/4$ (
$W = H/4$ ( $H$ is the sample height), and two-dimensional rectangles with aspect ratios
$H$ is the sample height), and two-dimensional rectangles with aspect ratios  $\varGamma \equiv L/H = 1$ and
$\varGamma \equiv L/H = 1$ and  $10$. The slip length
$10$. The slip length  $b$ for top and bottom plates varied from
$b$ for top and bottom plates varied from  $0$ to
$0$ to  $\infty$. The Rayleigh numbers
$\infty$. The Rayleigh numbers  $Ra$ were in the range
$Ra$ were in the range  $10^{6} \leqslant Ra \leqslant 10^{10}$ and the Prandtl number
$10^{6} \leqslant Ra \leqslant 10^{10}$ and the Prandtl number  $Pr$ was fixed at
$Pr$ was fixed at  $4.3$. As
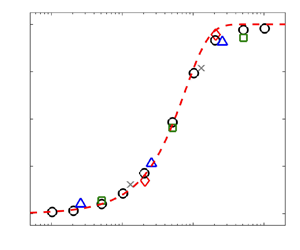
$4.3$. As  $b$ increases, the normalised
$b$ increases, the normalised  $Nu/Nu_0$ (
$Nu/Nu_0$ ( $Nu_0$ is the global heat transport for
$Nu_0$ is the global heat transport for  $b = 0$) from the three samples for different
$b = 0$) from the three samples for different  $Ra$ and
$Ra$ and  $\varGamma$ can be well described by the same function
$\varGamma$ can be well described by the same function  $Nu/Nu_0 = N_0 \tanh (b/\lambda _0) + 1$, with
$Nu/Nu_0 = N_0 \tanh (b/\lambda _0) + 1$, with  $N_0 = 0.8 \pm 0.03$. Here
$N_0 = 0.8 \pm 0.03$. Here  $\lambda _0 \equiv L/(2Nu_0)$ is the thermal boundary layer thickness for
$\lambda _0 \equiv L/(2Nu_0)$ is the thermal boundary layer thickness for  $b = 0$. Considering the BL fluctuations for
$b = 0$. Considering the BL fluctuations for  $Pr>1$, one can derive solutions of temperature profiles
$Pr>1$, one can derive solutions of temperature profiles  $\varTheta (z)$ and
$\varTheta (z)$ and  $\varOmega (z)$ near the thermal BL for
$\varOmega (z)$ near the thermal BL for  $b \geqslant 0$. When
$b \geqslant 0$. When  $b=0$, the solutions are equivalent to those reported by Shishkina et al. (Phys. Rev. Lett., vol. 114, 2015, 114302) and Wang et al. (Phys. Rev. Fluids, vol. 1, 2016, 082301(R)), respectively, for no-slip plates. For
$b=0$, the solutions are equivalent to those reported by Shishkina et al. (Phys. Rev. Lett., vol. 114, 2015, 114302) and Wang et al. (Phys. Rev. Fluids, vol. 1, 2016, 082301(R)), respectively, for no-slip plates. For  $b > 0$, the derived solutions are in excellent agreement with our DNS data for slippery plates.
$b > 0$, the derived solutions are in excellent agreement with our DNS data for slippery plates.