Abe, H., Kawamura, H. & Matsuo, Y.
2001
Direct numerical simulation of a fully developed turbulent channel flow with respect to the Reynolds number dependence. Trans. ASME J. Fluids Engng
123 (2), 382–393.
Alekseev, V. V., Gachechiladze, I. A., Kiknadze, G. I. & Oleinikov, V. G.
1998
Tornado-like energy transfer on three-dimensional concavities of reliefs-structure of self-organizing flow, their visualisation, and surface streamlining mechanisms. In Transactions of the 2nd Russian Nat. Conf. of Heat Transfer, Heat Transfer Intensification Radiation and Complex Heat Transfer, vol. 6, pp. 33–42. Publishing House of Moscow Energy Institute (MEI).
Balakumar, P. & Widnall, S. E.
1986
Application of unsteady aerodynamics to large-eddy breakup devices in a turbulent flow. Phys. Fluids
29 (6), 1779–1787.
Barthlott, W. & Neinhuis, C.
1997
Purity of the sacred lotus, or escape from contamination in biological surfaces. Planta
202 (1), 1–8.
Bechert, D. W. & Bartenwerfer, M.
1989
The viscous flow on surfaces with longitudinal ribs. J. Fluid Mech.
206, 105–129.
Bechert, D. W., Bruse, M. & Hage, W.
2000
Experiments with three-dimensional riblets as an idealized model of shark skin. Exp. Fluids
28 (5), 403–412.
Bechert, D. W., Bruse, M., Hage, W., Van Der Hoeven, J. G. T. & Hoppe, G.
1997
Experiments on drag-reducing surfaces and their optimization with an adjustable geometry. J. Fluid Mech.
338 (5), 59–87.
Burgess, N. K., Oliveira, M. M. & Ligrani, P. M.
2003
Nusselt number behavior on deep dimpled surfaces within a channel. Trans. ASME J. Heat Transfer
125, 11.
Cabal, A., Szumbarski, J. & Floryan, J. M.
2001
Numerical simulation of flows over corrugated walls. Comput. Fluids
30 (6), 753–776.
Chang, M. J., Chow, L. C. & Chang, W. S.
1991
Improved alternating-direction implicit method for solving transient three-dimensional heat diffusion problems. Numer. Heat Transfer B
19 (1), 69–84.
Chen, Y., Chew, Y. T. & Khoo, B. C.
2010
Turbulent flow manipulation by passive devices. In Proceedings of the 13th Asian Congress of Fluid Mechanics, pp. 613–616. The Asian Fluid Mechanics Committee (AFMC).
Choi, H., Moin, P. & Kim, J.
1993
Direct numerical simulation of turbulent flow over riblets. J. Fluid Mech.
255, 503–539.
Choi, K.-S.
1989
Near-wall structure of a turbulent boundary layer with riblets. J. Fluid Mech.
208, 417–458.
Choi, K.-S., Jukes, T. & Whalley, R.
2011
Turbulent boundary-layer control with plasma actuators. Phil. Trans. R. Soc. Lond. A
369 (1940), 1443–1458.
Daniello, R. J., Waterhouse, N. E. & Rothstein, J. P.
2009
Drag reduction in turbulent flows over superhydrophobic surfaces. Phys. Fluids
21 (8), 085103.
Darcy, H.
1857
Recherches Expérimentales Relatives au Mouvement de l’Eau dans les Tuyaux. Mallet-Bachelier.
Dean, B. & Bhushan, B.
2010
Shark-skin surfaces for fluid-drag reduction in turbulent flow: a review. Phil. Trans. R. Soc. Lond. A
368 (1929), 4775–4806.
Douglas, J.
1955
On the numerical integration of ∂
2
u/∂x
2 + ∂
2
u/∂y
2 = ∂u/∂t by implicit methods. J. Soc. Ind. Appl. Maths
3 (1), 42–45.
Eckert, E. R. G. & Irvine, T. F. Jr.
1956
Flow in corners of passages with noncircular cross sections. Trans. ASME
78 (4), 709.
Gao, L. C. & McCarthy, T. J.
2006
A perfectly hydrophobic surface (𝜃a/𝜃r = 180/180). J. Am. Chem. Soc.
128 (28), 9052–9053.
García-Mayoral, R. & Jiménez, J.
2011
Drag reduction by riblets. Phil. Trans. R. Soc. Lond. A
369 (1940), 1412–1427.
Graham, J. M. R.
1998
The effect of a two-dimensional cascade of thin streamwise plates on homogeneous turbulence. J. Fluid Mech.
356, 125–147.
Hagen, G.
1854
Uber den einfluss der temperatur auf die bewegung des wasser in röhren. Math. Abh. Akad. Wiss.
17.
Hoepffner, J. & Fukagata, K.
2009
Pumping or drag reduction?
J. Fluid Mech.
635, 171–187.
Incropera, F. P. & DeWitt, D. P.
2002
Fundamentals of Heat and Mass Transfer, 5th edn. Wiley.
Itoh, M., Tamano, S., Iguchi, R., Yokota, K., Akino, N., Hino, R. & Kubo, S.
2006
Turbulent drag reduction by the seal fur surface. Phys. Fluids
18, 065102.
Iuso, G., Onorato, M., Spazzini, P. G. & Di Cicca, G. M.
2002
Wall turbulence manipulation by large-scale streamwise vortices. J. Fluid Mech.
473, 23–58.
Joseph, P., Cottin-Bizonne, C., Benoit, J.-M., Ybert, C., Journet, C., Tabeling, P. & Bocquet, L.
2006
Slippage of water past superhydrophobic carbon nanotube forests in microchannels. Phys. Rev. Lett.
97 (15), 156104.
Keating, A. & Piomelli, U.
2006
A dynamic stochastic forcing method as a wall-layer model for large-eddy simulation. J. Turbul.
7, N12.
Kim, J.
2011
Physics and control of wall turbulence for drag reduction. Phil. Trans. R. Soc. Lond. A
369 (1940), 1396–1411.
Kim, J., Moin, P. & Moser, R.
1987
Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech.
177, 133–166.
Lienhart, H., Breuer, M. & Köksoy, C.
2008
Drag reduction by dimples?-a complementary experimental/numerical investigation. Intl J. Heat Fluid Flow
29 (3), 783–791.
Martell, M., Perot, J. B. & Rothstein, J. P.
2009
Direct numerical simulations of turbulent flows over superhydrophobic surfaces. J. Fluid Mech.
620, 31–41.
Min, T., Kang, S. M., Speyer, J. L. & Kim, J.
2006
Sustained sub-laminar drag in a fully developed channel flow. J. Fluid Mech.
558, 309–318.
Mohammadi, A. & Floryan, J. M.
2015
Numerical analysis of laminar-drag-reducing grooves. Trans. ASME J. Fluids Engng
137 (4), 041201.
Mohammadi, M. & Floryan, J. M.
2013a
Groove optimization for drag reduction. Phys. Fluids
25 (11), 113601.
Mohammadi, M. & Floryan, J. M.
2013b
Pressure losses in grooved channels. J. Fluid Mech.
725, 23–54.
Moin, P. & Kim, J.
1982
Numerical investigation of turbulent channel flow. J. Fluid Mech.
118, 341–377.
Moody, L. F.
1944
Friction factors for pipe flow. Trans. ASME
66 (8), 671–684.
Moradi, H. V. & Floryan, J. M.
2013
Flows in annuli with longitudinal grooves. J. Fluid Mech.
716, 280–315.
Moser, R. D., Kim, J. & Mansour, N. N.
1999
Direct numerical simulation of turbulent channel flow up to Re
𝜏 = 590. Phys. Fluids
11, 943.
Nikuradse, J.1933 Strömungsgesetze in rauhen rohren. VDI-Forschungscheft 361; also NACA TM 1292 (1950).
Ou, J., Perot, B. & Rothstein, J. P.
2004
Laminar drag reduction in microchannels using ultrahydrophobic surfaces. Phys. Fluids
16 (12), 4635–4643.
Ou, J. & Rothstein, J. P.
2005
Direct velocity measurements of the flow past drag-reducing ultrahydrophobic surfaces. Phys. Fluids
17 (10), 103606.
Park, H. W., Park, H. M. & Kim, J.
2013
A numerical study of the effects of superhydrophobic surface on skin-friction drag in turbulent channel flow. Phys. Fluids
25 (11), 110815.
Pope, S. B.
2000
Turbulent Flows. Cambridge University Press.
Quadrio, M.
2011
Drag reduction in turbulent boundary layers by in-plane wall motion. Phil. Trans. R. Soc. Lond. A
369 (1940), 1428–1442.
Quadrio, M., Floryan, J. M. & Luchini, P.
2007
Effect of streamwise-periodic wall transpiration on turbulent friction drag. J. Fluid Mech.
576, 425–444.
Quéré, D.
2008
Wetting and roughness. Annu. Rev. Mater. Res.
38, 71–99.
Reyssat, M., Yeomans, J. M. & Quéré, D.
2008
Impalement of fakir drops. Europhys. Lett.
81, 26006.
Rothstein, J. P.
2010
Slip on superhydrophobic surfaces. Annu. Rev. Fluid Mech.
42, 89–109.
Sagong, W., Kim, C., Choi, S., Jeon, W. P. & Choi, H.
2008
Does the sailfish skin reduce the skin friction like the shark skin?
Phys. Fluids
20, 101510.
Sahlin, A., Alfredsson, P. H. & Johansson, A. V.
1986
Direct drag measurements for a flat plate with passive boundary layer manipulators. Phys. Fluids
29 (3), 696–700.
Sahlin, A., Johansson, A. V. & Alfredsson, P. H.
1988
The possibility of drag reduction by outer layer manipulators in turbulent boundary layers. Phys. Fluids
31 (10), 2814–2820.
Samaha, M. A., Tafreshi, H. V. & Gad-el Hak, M.
2011
Modeling drag reduction and meniscus stability of superhydrophobic surfaces comprised of random roughness. Phys. Fluids
23 (1), 012001.
Savill, A. M. & Mumford, J. C.
1988
Manipulation of turbulent boundary layers by outer-layer devices: skin-friction and flow-visualization results. J. Fluid Mech.
191, 389–418.
Schoppa, W. & Hussain, F.
1998
A large-scale control strategy for drag reduction in turbulent boundary layers. Phys. Fluids
10, 1049.
Shur, M., Spalart, P. R., Strelets, M. & Travin, A.
1999
Detached-eddy simulation of an airfoil at high angle of attack. In Fourth International Symposium on Engineering Turbulence Modelling and Experiments, pp. 669–678. Elsevier.
Sirovich, L. & Karlsson, S.
1997
Turbulent drag reduction by passive mechanisms. Nature
388, 753–755.
Spalart, P. R. & Allmaras, S. R.
1992
A one-equation turbulence model for aerodynamic flows. AIAA Paper 1992-04-39
1 (2), 5–21.
Spalart, P. R., Jou, W. H. & Allmaras, M. S. S. R.
1997
Comments on the feasibility of les for wings and on hybrid RANS/LES approach. In Proceedings of the First AFOSR International Conference on DNS/LES, p. 137. Greyden Press.
Sudo, S., Tsuyuki, K., Ito, Y. & Ikohagi, T.
2002
A study on the surface shape of fish scales. JSME Intl J. C
45 (4), 1100–1105.
Tay, C. M. J., Khoo, B. C. & Chew, Y. T.
2015
Mechanics of drag reduction by shallow dimples in channel flow. Phys. Fluids
27 (3), 035109.
Truesdell, R., Mammoli, A., Vorobieff, P., van Swol, F. & Brinker, C. J.
2006
Drag reduction on a patterned superhydrophobic surface. Phys. Rev. Lett.
97 (4), 044504.
Tu, S., Aliabadi, S., Patel, R. & Watts, M.
2009
An implementation of the Spalart–Allmaras DES model in an implicit unstructured hybrid finite volume/element solver for incompressible turbulent flow. Intl J. Numer. Meth. Fluids
59 (9), 1051–1062.
Veldhuis, L. L. M. & Vervoort, E.2009 Drag effect of a dented surface in a turbulent flow. AIAA Paper 2009-3950; San Antonio, Texas.
Walsh, M. J.
1980
Drag characteristics of V-groove and transverse curvature riblets. In Viscous Flow Drag Reduction, pp. 168–184. AIAA.
Walsh, M. J.
1983
Riblets as a viscous drag reduction technique. AIAA J.
21, 485–486.
Walsh, M. J. & Lindeman, A. M.1984 Optimization and application of riblets for turbulent drag reduction. AIAA Paper 84-0347.
Walsh, M. J. & Weinstein, L. M.1978 Drag and heat transfer on surfaces with small longitudinal fins. AIAA Paper 78-1161.
Wang, Z., Yeo, K. S. & Khoo, B. C.
2006
DNS of low Reynolds number turbulent flows in dimpled channels. J. Turbul.
7, 37.
Wesseling, P. & Oosterlee, C. W.
2001
Geometric multigrid with applications to computational fluid dynamics. J. Comput. Appl. Maths
128 (1–2), 311–334.
Zhang, X., Shi, F., Niu, J., Jiang, Y. G. & Wang, Z. Q.
2008
Superhydrophobic surfaces: from structural control to functional application. J. Mater. Chem.
18 (6), 621–633.
Zhou, M., Li, J., Wu, C. X., Zhou, X. K. & Cai, L.
2011
Fluid drag reduction on superhydrophobic surfaces coated with carbon nanotube forests (cnts). Soft Matt.
7 (9), 4391–4396.
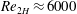$Re_{2H}\approx 6000$
) using both analytical and numerical methodologies. The results demonstrate that the long-wavelength grooves can increase discharge by 20 %–150 %, depending on the groove amplitude and the type of flow, while the short-wavelength grooves reduce the discharge. It has been shown that the reduced geometry model applies to the analysis of turbulent flows and the performance of grooves of arbitrary form is well approximated by the performance of grooves whose shape is represented by the dominant Fourier mode. The flow patterns, the turbulent kinetic energy as well as the Reynolds stresses were examined to identify the mechanisms leading to an increase in discharge. It is shown that the increase in discharge results from the rearrangement of the bulk fluid movement and not from the suppression of turbulence intensity. The turbulent kinetic energy and the Reynolds stresses are rearranged while their volume-averaged intensities remain the same as in the smooth channel. Analysis of the interaction of the groove patterns on both walls demonstrates that the converging–diverging configuration results in the greatest increase in discharge while the wavy channel configuration results in a reduction in discharge.
