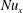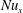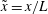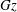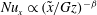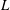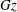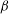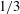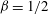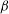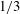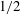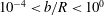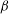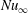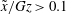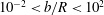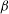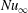1. Introduction
The classical Graetz–Nusselt problem concerns a fluid of uniform temperature
![]() $T_{0}$
flowing in an insulated cylindrical tube. The flow is laminar and hydrodynamically fully developed, and has constant physical properties (see figure 1). At
$T_{0}$
flowing in an insulated cylindrical tube. The flow is laminar and hydrodynamically fully developed, and has constant physical properties (see figure 1). At
![]() $x=0$
the fluid enters a tube section with a constant wall temperature
$x=0$
the fluid enters a tube section with a constant wall temperature
![]() $T_{1}$
. Neglecting viscous dissipation and axial heat conduction, Graetz (Reference Graetz1882, Reference Graetz1885) and Nusselt (Reference Nusselt1910) independently found a mathematical solution to this problem, describing the temperature profile for
$T_{1}$
. Neglecting viscous dissipation and axial heat conduction, Graetz (Reference Graetz1882, Reference Graetz1885) and Nusselt (Reference Nusselt1910) independently found a mathematical solution to this problem, describing the temperature profile for
![]() $x>0$
. The problem was solved for both a uniform (Graetz Reference Graetz1882) and a parabolic (Graetz Reference Graetz1885; Nusselt Reference Nusselt1910) fluid velocity profile. From the temperature distribution the local heat flux at the wall can be obtained, which is commonly expressed by the local Nusselt number
$x>0$
. The problem was solved for both a uniform (Graetz Reference Graetz1882) and a parabolic (Graetz Reference Graetz1885; Nusselt Reference Nusselt1910) fluid velocity profile. From the temperature distribution the local heat flux at the wall can be obtained, which is commonly expressed by the local Nusselt number
![]() $\mathit{Nu}_{x}$
, a dimensionless heat transfer coefficient (Eckert & Drake Reference Eckert and Drake1972; Bird, Stewart & Lightfoot Reference Bird, Stewart and Lightfoot2007). The Nusselt number
$\mathit{Nu}_{x}$
, a dimensionless heat transfer coefficient (Eckert & Drake Reference Eckert and Drake1972; Bird, Stewart & Lightfoot Reference Bird, Stewart and Lightfoot2007). The Nusselt number
where
![]() $h_{x}$
is the local heat transfer coefficient,
$h_{x}$
is the local heat transfer coefficient,
![]() $D=2R$
is the diameter of the tube and
$D=2R$
is the diameter of the tube and
![]() $k$
is the thermal conductivity, can be interpreted as the ratio of convective to conductive radial heat transfer (Jakob Reference Jakob1949; Shah & London Reference Shah and London1978). The Nusselt number
$k$
is the thermal conductivity, can be interpreted as the ratio of convective to conductive radial heat transfer (Jakob Reference Jakob1949; Shah & London Reference Shah and London1978). The Nusselt number
![]() $\mathit{Nu}_{x}$
is a function of the dimensionless downstream position
$\mathit{Nu}_{x}$
is a function of the dimensionless downstream position
![]() $\tilde{x}=x/L$
,
$\tilde{x}=x/L$
,
![]() $L$
being the length of the non-insulated section of the tube, and the Graetz number
$L$
being the length of the non-insulated section of the tube, and the Graetz number
![]() $\mathit{Gz}$
only. The Graetz number is defined as (Jakob Reference Jakob1949; Shah & London Reference Shah and London1978)
$\mathit{Gz}$
only. The Graetz number is defined as (Jakob Reference Jakob1949; Shah & London Reference Shah and London1978)
where
![]() $u_{av}$
is the average fluid velocity and
$u_{av}$
is the average fluid velocity and
![]() ${\it\alpha}$
is the thermal diffusivity. It is the product of the Reynolds number
${\it\alpha}$
is the thermal diffusivity. It is the product of the Reynolds number
![]() $\mathit{Re}=u_{av}D/{\it\nu}$
, the Prandtl number
$\mathit{Re}=u_{av}D/{\it\nu}$
, the Prandtl number
![]() $\mathit{Pr}={\it\nu}/{\it\alpha}$
and the ratio
$\mathit{Pr}={\it\nu}/{\it\alpha}$
and the ratio
![]() $D/L$
, and can be interpreted as the ratio of axial advective to radial diffusive heat transport.
$D/L$
, and can be interpreted as the ratio of axial advective to radial diffusive heat transport.

Figure 1. The Graetz–Nusselt problem concerns transport of heat between a hydrodynamically fully developed fluid flow with
![]() ${\rm\Theta}=(T_{1}-T)/(T_{1}-T_{0})=1$
and a tube with a constant wall temperature
${\rm\Theta}=(T_{1}-T)/(T_{1}-T_{0})=1$
and a tube with a constant wall temperature
![]() ${\rm\Theta}=0$
for
${\rm\Theta}=0$
for
![]() $\tilde{x}>0$
. The velocity profile of the inflowing fluid is a function of the tube radius
$\tilde{x}>0$
. The velocity profile of the inflowing fluid is a function of the tube radius
![]() $\tilde{r}$
and the slip length
$\tilde{r}$
and the slip length
![]() $\tilde{b}$
, where
$\tilde{b}$
, where
![]() $0\leqslant \tilde{b}\leqslant \infty$
. The profile is parabolic for
$0\leqslant \tilde{b}\leqslant \infty$
. The profile is parabolic for
![]() $\tilde{b}=0$
and uniform for
$\tilde{b}=0$
and uniform for
![]() $\tilde{b}=\infty$
. The contour map gives an example of a temperature profile.
$\tilde{b}=\infty$
. The contour map gives an example of a temperature profile.
The temperature profiles found by Graetz and Nusselt involve infinite series in terms of eigenvalues and eigenfunctions. When
![]() $\tilde{x}/\mathit{Gz}>0.1$
, the first terms of the series solutions dominate. This results in a developed Nusselt number
$\tilde{x}/\mathit{Gz}>0.1$
, the first terms of the series solutions dominate. This results in a developed Nusselt number
![]() $\mathit{Nu}_{\infty }=3.66$
for parabolic flow and
$\mathit{Nu}_{\infty }=3.66$
for parabolic flow and
![]() $\mathit{Nu}_{\infty }=5.78$
for plug flow (Shah & London Reference Shah and London1978). The flow is said to be thermally fully developed. For
$\mathit{Nu}_{\infty }=5.78$
for plug flow (Shah & London Reference Shah and London1978). The flow is said to be thermally fully developed. For
![]() $\tilde{x}/\mathit{Gz}<0.01$
, when the flow is thermally developing, and in particular when
$\tilde{x}/\mathit{Gz}<0.01$
, when the flow is thermally developing, and in particular when
![]() $x\rightarrow 0$
, a very large number of terms are required to obtain the Nusselt number with sufficient accuracy. Lévêque (Reference Lévêque1928) circumvented this problem by assuming that in the entrance region the thermal boundary layer is thin compared with the viscous boundary layer (Eckert & Drake Reference Eckert and Drake1972; Shah & London Reference Shah and London1978; Bird et al.
Reference Bird, Stewart and Lightfoot2007). In that case curvature effects can be neglected. Furthermore, it can be assumed that the bulk extends to infinity, and that the velocity profile is linear. Lévêque showed that
$x\rightarrow 0$
, a very large number of terms are required to obtain the Nusselt number with sufficient accuracy. Lévêque (Reference Lévêque1928) circumvented this problem by assuming that in the entrance region the thermal boundary layer is thin compared with the viscous boundary layer (Eckert & Drake Reference Eckert and Drake1972; Shah & London Reference Shah and London1978; Bird et al.
Reference Bird, Stewart and Lightfoot2007). In that case curvature effects can be neglected. Furthermore, it can be assumed that the bulk extends to infinity, and that the velocity profile is linear. Lévêque showed that
with
![]() ${\it\beta}=1/3$
for a parabolic velocity profile and
${\it\beta}=1/3$
for a parabolic velocity profile and
![]() ${\it\beta}=1/2$
for a uniform velocity profile. Essentially, complete solutions for the Graetz–Nusselt problem found in the literature are a combination of the methods of Graetz and Lévêque (Shah & London Reference Shah and London1978).
${\it\beta}=1/2$
for a uniform velocity profile. Essentially, complete solutions for the Graetz–Nusselt problem found in the literature are a combination of the methods of Graetz and Lévêque (Shah & London Reference Shah and London1978).
There are special cases where the no-slip or the no-shear boundary condition does not hold. The effects of slip phenomena encountered in rarefied gas flows, which include velocity and temperature jumps at the tube wall (Eckert & Drake Reference Eckert and Drake1972; Karniadakis, Beskok & Aluru Reference Karniadakis, Beskok and Aluru2005), were first investigated by Sparrow & Lin (Reference Sparrow and Lin1962). Both wall slip and temperature jump are a function of the Knudsen number
![]() $\mathit{Kn}$
, the ratio of mean free path to tube diameter. Their results show that
$\mathit{Kn}$
, the ratio of mean free path to tube diameter. Their results show that
![]() $\mathit{Nu}_{\infty }$
decreases with increasing mean free path, which implies increasing wall slip and larger temperature jumps. Barron et al. (Reference Barron, Wang, Ameel and Warrington1997) found that, for a given Graetz number, the Nusselt number becomes larger with increasing slip. Although they explicitly incorporated the temperature jump in the boundary conditions, it was ignored in the calculation of the eigenvalues (Ezquerra Larrodé, Housiadas & Drossinos Reference Ezquerra Larrodé, Housiadas and Drossinos2000). It is crucial to account for the temperature jump at the wall for rarefied gas flows, since the effect of this temperature jump is dominant over the influence of wall slip (Ezquerra Larrodé et al.
Reference Ezquerra Larrodé, Housiadas and Drossinos2000; Colin Reference Colin2011).
$\mathit{Nu}_{\infty }$
decreases with increasing mean free path, which implies increasing wall slip and larger temperature jumps. Barron et al. (Reference Barron, Wang, Ameel and Warrington1997) found that, for a given Graetz number, the Nusselt number becomes larger with increasing slip. Although they explicitly incorporated the temperature jump in the boundary conditions, it was ignored in the calculation of the eigenvalues (Ezquerra Larrodé, Housiadas & Drossinos Reference Ezquerra Larrodé, Housiadas and Drossinos2000). It is crucial to account for the temperature jump at the wall for rarefied gas flows, since the effect of this temperature jump is dominant over the influence of wall slip (Ezquerra Larrodé et al.
Reference Ezquerra Larrodé, Housiadas and Drossinos2000; Colin Reference Colin2011).
In continuum flows, i.e. liquid and gas flows for which
![]() $\mathit{Kn}<10^{-2}$
, a temperature jump is not present (Eckert & Drake Reference Eckert and Drake1972; Karniadakis et al.
Reference Karniadakis, Beskok and Aluru2005). Moreover, in most situations the no-slip boundary condition is correct (Eckert & Drake Reference Eckert and Drake1972; Lauga, Brenner & Stone Reference Lauga, Brenner, Stone, Tropea, Yarin and Foss2007). However, with the rise of micro- and nanofluidics it became apparent that the no-slip boundary condition for liquid flows does not always hold (Lauga et al.
Reference Lauga, Brenner, Stone, Tropea, Yarin and Foss2007). Intrinsic slip lengths vary from nearly zero (Bocquet & Barrat Reference Bocquet and Barrat2007; Rothstein Reference Rothstein2010) to almost infinity (Whitby & Quirke Reference Whitby and Quirke2007; Majumder, Chopra & Hinds Reference Majumder, Chopra and Hinds2011). Here, the slip length is defined by Navier’s slip condition (Navier Reference Navier1823),
$\mathit{Kn}<10^{-2}$
, a temperature jump is not present (Eckert & Drake Reference Eckert and Drake1972; Karniadakis et al.
Reference Karniadakis, Beskok and Aluru2005). Moreover, in most situations the no-slip boundary condition is correct (Eckert & Drake Reference Eckert and Drake1972; Lauga, Brenner & Stone Reference Lauga, Brenner, Stone, Tropea, Yarin and Foss2007). However, with the rise of micro- and nanofluidics it became apparent that the no-slip boundary condition for liquid flows does not always hold (Lauga et al.
Reference Lauga, Brenner, Stone, Tropea, Yarin and Foss2007). Intrinsic slip lengths vary from nearly zero (Bocquet & Barrat Reference Bocquet and Barrat2007; Rothstein Reference Rothstein2010) to almost infinity (Whitby & Quirke Reference Whitby and Quirke2007; Majumder, Chopra & Hinds Reference Majumder, Chopra and Hinds2011). Here, the slip length is defined by Navier’s slip condition (Navier Reference Navier1823),
which states that the liquid velocity at the wall
![]() $u_{s}$
is proportional to the slip length
$u_{s}$
is proportional to the slip length
![]() $b$
and the velocity gradient
$b$
and the velocity gradient
![]() $\partial _{r}u$
at the wall. This implies that the classical Graetz–Nusselt solutions are not applicable to this type of flow.
$\partial _{r}u$
at the wall. This implies that the classical Graetz–Nusselt solutions are not applicable to this type of flow.
In this paper we present numerical and analytical solutions to the Graetz–Nusselt problem for continuum flows with finite slip. The effects of wall slip on both the exponent
![]() ${\it\beta}$
and
${\it\beta}$
and
![]() $\mathit{Nu}_{\infty }$
, characteristic for heat transport in the thermally developing and thermally developed regimes, are investigated. The results reveal distinct transition points for
$\mathit{Nu}_{\infty }$
, characteristic for heat transport in the thermally developing and thermally developed regimes, are investigated. The results reveal distinct transition points for
![]() ${\it\beta}$
and
${\it\beta}$
and
![]() $\mathit{Nu}_{\infty }$
when the slip length
$\mathit{Nu}_{\infty }$
when the slip length
![]() $b$
goes from zero to infinity. These transition points are explained both mathematically and physically.
$b$
goes from zero to infinity. These transition points are explained both mathematically and physically.
2. Mathematical model
2.1. Heat equation
A schematic representation of the Graetz–Nusselt problem is provided in figure 1. Here, under the assumptions given in § 1, the governing equation describing stationary heat transport in a cylindrical system can be written as
where
![]() $u(r,b)$
describes the velocity profile of the laminar fluid flow in the
$u(r,b)$
describes the velocity profile of the laminar fluid flow in the
![]() $x$
-direction. The boundary conditions are
$x$
-direction. The boundary conditions are
![]() $T(0,r)=T_{0}$
and
$T(0,r)=T_{0}$
and
![]() $T(x,R)=T_{1}$
. At
$T(x,R)=T_{1}$
. At
![]() $x=0$
, the flow is hydrodynamically fully developed. Solution of the Navier–Stokes equation for stationary slip flow in the axial direction yields the following expression for the velocity profile:
$x=0$
, the flow is hydrodynamically fully developed. Solution of the Navier–Stokes equation for stationary slip flow in the axial direction yields the following expression for the velocity profile:
where
![]() $\tilde{u} =u/u_{av}$
,
$\tilde{u} =u/u_{av}$
,
![]() $\tilde{r}=r/R$
and
$\tilde{r}=r/R$
and
![]() $\tilde{b}=b/R$
. Here,
$\tilde{b}=b/R$
. Here,
![]() $\tilde{u}$
can be interpreted as the sum of the variable velocity
$\tilde{u}$
can be interpreted as the sum of the variable velocity
![]() $\tilde{u} _{v}(\tilde{r},\tilde{b})=2(1-\tilde{r}^{2})/(1+4\tilde{b})$
and the slip velocity
$\tilde{u} _{v}(\tilde{r},\tilde{b})=2(1-\tilde{r}^{2})/(1+4\tilde{b})$
and the slip velocity
![]() $\tilde{u} _{s}(\tilde{b})=4\tilde{b}/(1+4\tilde{b})$
. The heat equation can now be non-dimensionalised using
$\tilde{u} _{s}(\tilde{b})=4\tilde{b}/(1+4\tilde{b})$
. The heat equation can now be non-dimensionalised using
![]() ${\rm\Theta}=(T_{1}-T)/(T_{1}-T_{0})$
and
${\rm\Theta}=(T_{1}-T)/(T_{1}-T_{0})$
and
![]() $\tilde{x}=x/L$
,
$\tilde{x}=x/L$
,
with
![]() ${\rm\Theta}(0,\tilde{r})=1$
and
${\rm\Theta}(0,\tilde{r})=1$
and
![]() ${\rm\Theta}(\tilde{x},1)=0$
.
${\rm\Theta}(\tilde{x},1)=0$
.
2.2. Nusselt number
Using Fourier’s law of thermal conduction, the local heat transfer coefficient
![]() $h_{x}$
can be written as
$h_{x}$
can be written as
![]() $h_{x}=-k/(\left\langle T\right\rangle -T_{1})\left.\partial _{r}T\right|_{r=R}$
(full mathematical and numerical details are given in the supplementary data available at http://dx.doi.org/10.1017/jfm.2014.733). By rewriting the temperature gradient in dimensionless form using the dimensionless flow-averaged temperature
$h_{x}=-k/(\left\langle T\right\rangle -T_{1})\left.\partial _{r}T\right|_{r=R}$
(full mathematical and numerical details are given in the supplementary data available at http://dx.doi.org/10.1017/jfm.2014.733). By rewriting the temperature gradient in dimensionless form using the dimensionless flow-averaged temperature
![]() $\left\langle {\rm\Theta}\right\rangle =(T_{1}-\left\langle T\right\rangle )/(T_{1}-T_{0})$
, we find for the local Nusselt number that
$\left\langle {\rm\Theta}\right\rangle =(T_{1}-\left\langle T\right\rangle )/(T_{1}-T_{0})$
, we find for the local Nusselt number that
When
![]() $\tilde{x}/\mathit{Gz}>0.1$
,
$\tilde{x}/\mathit{Gz}>0.1$
,
![]() $\mathit{Nu}_{x}\rightarrow \mathit{Nu}_{\infty }$
.
$\mathit{Nu}_{x}\rightarrow \mathit{Nu}_{\infty }$
.
2.3. Analytical expressions for thermally developing flow
To find an analytical expression for
![]() $\mathit{Nu}_{x}$
near the entrance of the pipe, the Lévêque approximation is followed. In that case, the governing equation can be solved in a two-dimensional Cartesian coordinate system:
$\mathit{Nu}_{x}$
near the entrance of the pipe, the Lévêque approximation is followed. In that case, the governing equation can be solved in a two-dimensional Cartesian coordinate system:
Here, the wall is located at
![]() $y=0$
, i.e. the direction of the
$y=0$
, i.e. the direction of the
![]() $y$
-axis is the reverse of that of the
$y$
-axis is the reverse of that of the
![]() $r$
-axis. Then, with
$r$
-axis. Then, with
![]() ${\tilde{y}}=y/R$
, the velocity profile becomes
${\tilde{y}}=y/R$
, the velocity profile becomes
![]() $\tilde{u} =4({\tilde{y}}+\tilde{b})/(1+4\tilde{b})$
.
$\tilde{u} =4({\tilde{y}}+\tilde{b})/(1+4\tilde{b})$
.
The analytical expressions for
![]() $\mathit{Nu}_{x}$
for no-slip and no-shear flow are known (Bird et al.
Reference Bird, Stewart and Lightfoot2007). For
$\mathit{Nu}_{x}$
for no-slip and no-shear flow are known (Bird et al.
Reference Bird, Stewart and Lightfoot2007). For
![]() $\tilde{b}=0$
one can derive that
$\tilde{b}=0$
one can derive that
where
![]() ${\rm\Gamma}$
denotes the gamma function. For no-shear flow, i.e.
${\rm\Gamma}$
denotes the gamma function. For no-shear flow, i.e.
![]() $b=\infty$
, one finds
$b=\infty$
, one finds
Thus,
![]() ${\it\beta}=1/3$
for parabolic flow and
${\it\beta}=1/3$
for parabolic flow and
![]() ${\it\beta}=1/2$
for uniform flow.
${\it\beta}=1/2$
for uniform flow.
To arrive at an analytical expression for
![]() $\mathit{Nu}_{x}$
for finite slip (i.e.
$\mathit{Nu}_{x}$
for finite slip (i.e.
![]() $0<\tilde{b}<\infty$
), (2.5) is non-dimensionalised using
$0<\tilde{b}<\infty$
), (2.5) is non-dimensionalised using
![]() $Y=y/b$
and
$Y=y/b$
and
![]() $X=x{\it\alpha}(R+4b)/(4u_{av}b^{3})=(\tilde{x}/\mathit{Gz})(1+4\tilde{b})/\tilde{b}^{3}$
. This gives
$X=x{\it\alpha}(R+4b)/(4u_{av}b^{3})=(\tilde{x}/\mathit{Gz})(1+4\tilde{b})/\tilde{b}^{3}$
. This gives
with
![]() ${\rm\Theta}(0,Y)=1$
,
${\rm\Theta}(0,Y)=1$
,
![]() ${\rm\Theta}(X,0)=0$
and
${\rm\Theta}(X,0)=0$
and
![]() ${\rm\Theta}(X,\infty )=1$
. To reduce the number of variables, we perform the Laplace transformation
${\rm\Theta}(X,\infty )=1$
. To reduce the number of variables, we perform the Laplace transformation
where
![]() $\bar{{\rm\Theta}}$
is the Laplace transform of
$\bar{{\rm\Theta}}$
is the Laplace transform of
![]() ${\rm\Theta}$
. Furthermore,
${\rm\Theta}$
. Furthermore,
![]() $\mathscr{L}_{X}[\partial _{Y}^{2}{\rm\Theta}]=\partial _{Y}^{2}\bar{{\rm\Theta}}$
. The governing equation now becomes
$\mathscr{L}_{X}[\partial _{Y}^{2}{\rm\Theta}]=\partial _{Y}^{2}\bar{{\rm\Theta}}$
. The governing equation now becomes
with
![]() $\bar{{\rm\Theta}}(p,0)=0$
and
$\bar{{\rm\Theta}}(p,0)=0$
and
![]() $\bar{{\rm\Theta}}(p,\infty )=1/p$
. Introduction of
$\bar{{\rm\Theta}}(p,\infty )=1/p$
. Introduction of
![]() $\hat{{\rm\Theta}}=\bar{{\rm\Theta}}-1/p$
and subsequent rewriting yields
$\hat{{\rm\Theta}}=\bar{{\rm\Theta}}-1/p$
and subsequent rewriting yields
with
![]() $\hat{{\rm\Theta}}(p,0)=-1/p$
and
$\hat{{\rm\Theta}}(p,0)=-1/p$
and
![]() $\hat{{\rm\Theta}}(p,\infty )=0$
. To convert this expression into an ordinary differential equation (ODE), we define
$\hat{{\rm\Theta}}(p,\infty )=0$
. To convert this expression into an ordinary differential equation (ODE), we define
![]() ${\it\eta}=p^{1/3}(1+Y)$
. Now the Airy equation is found,
${\it\eta}=p^{1/3}(1+Y)$
. Now the Airy equation is found,
with
![]() $\hat{{\rm\Theta}}(p^{1/3})=-1/p$
and
$\hat{{\rm\Theta}}(p^{1/3})=-1/p$
and
![]() $\hat{{\rm\Theta}}(\infty )=0$
. Its general solution of the first kind is the Airy function
$\hat{{\rm\Theta}}(\infty )=0$
. Its general solution of the first kind is the Airy function
![]() $\text{Ai}({\it\eta})$
, with
$\text{Ai}({\it\eta})$
, with
![]() $\lim _{{\it\eta}\rightarrow \infty }\text{Ai}({\it\eta})=0$
. Then the solutions for
$\lim _{{\it\eta}\rightarrow \infty }\text{Ai}({\it\eta})=0$
. Then the solutions for
![]() $\hat{{\rm\Theta}}$
and
$\hat{{\rm\Theta}}$
and
![]() $\bar{{\rm\Theta}}$
become
$\bar{{\rm\Theta}}$
become
To obtain
![]() ${\rm\Theta}$
, we take the inverse Laplace transform in
${\rm\Theta}$
, we take the inverse Laplace transform in
![]() $X$
, giving
$X$
, giving
For
![]() $\mathit{Nu}_{x}$
we can derive that, given that
$\mathit{Nu}_{x}$
we can derive that, given that
![]() $\left\langle {\rm\Theta}\right\rangle =1$
following the Lévêque approximation,
$\left\langle {\rm\Theta}\right\rangle =1$
following the Lévêque approximation,
Then, finally, we obtain
The function
![]() $g(X)$
is universal, as it does not depend on
$g(X)$
is universal, as it does not depend on
![]() $\tilde{b}$
. The slip length affects the scaling between
$\tilde{b}$
. The slip length affects the scaling between
![]() $X$
and
$X$
and
![]() $\tilde{x}/\mathit{Gz}$
, so it determines which part of the function
$\tilde{x}/\mathit{Gz}$
, so it determines which part of the function
![]() $g(X)$
is relevant. The supplementary information provides a description of how to evaluate
$g(X)$
is relevant. The supplementary information provides a description of how to evaluate
![]() $g(X)$
.
$g(X)$
.
2.4. Thermal and viscous boundary layer thickness
The thermal boundary layer thickness
![]() $\tilde{{\it\lambda}}_{T}$
is defined as
$\tilde{{\it\lambda}}_{T}$
is defined as
![]() $\tilde{{\it\lambda}}_{T}=1-\tilde{r}({\rm\Theta}=0.99)$
. When
$\tilde{{\it\lambda}}_{T}=1-\tilde{r}({\rm\Theta}=0.99)$
. When
![]() ${\rm\Theta}(\tilde{x}/\mathit{Gz},0)<0.99$
,
${\rm\Theta}(\tilde{x}/\mathit{Gz},0)<0.99$
,
![]() $\tilde{{\it\lambda}}_{T}=1$
.
$\tilde{{\it\lambda}}_{T}=1$
.
The viscous boundary layer
![]() $\tilde{{\it\delta}}_{{\it\nu}}$
is defined as follows. It corresponds to the point
$\tilde{{\it\delta}}_{{\it\nu}}$
is defined as follows. It corresponds to the point
![]() $\tilde{r}=1-\tilde{{\it\delta}}_{{\it\nu}}$
where the parabolic velocity component
$\tilde{r}=1-\tilde{{\it\delta}}_{{\it\nu}}$
where the parabolic velocity component
![]() $\tilde{u} _{v}(\tilde{r})$
equals
$\tilde{u} _{v}(\tilde{r})$
equals
![]() $c$
times the slip velocity
$c$
times the slip velocity
![]() $\tilde{u} _{s}$
at the wall. Thus,
$\tilde{u} _{s}$
at the wall. Thus,
![]() $\tilde{{\it\delta}}_{{\it\nu}}(\tilde{u} _{v}=c\tilde{u} _{s})=1-(1-2c\tilde{b})^{1/2}$
. When
$\tilde{{\it\delta}}_{{\it\nu}}(\tilde{u} _{v}=c\tilde{u} _{s})=1-(1-2c\tilde{b})^{1/2}$
. When
![]() $\tilde{b}\geqslant 1/(2c)$
,
$\tilde{b}\geqslant 1/(2c)$
,
![]() $\tilde{{\it\delta}}_{{\it\nu}}=1$
. It should be noted that, for a given
$\tilde{{\it\delta}}_{{\it\nu}}=1$
. It should be noted that, for a given
![]() $\tilde{b}$
and
$\tilde{b}$
and
![]() $c$
,
$c$
,
![]() $\tilde{{\it\delta}}_{{\it\nu}}$
is fixed for all
$\tilde{{\it\delta}}_{{\it\nu}}$
is fixed for all
![]() $\tilde{x}/\mathit{Gz}$
, while
$\tilde{x}/\mathit{Gz}$
, while
![]() $\tilde{{\it\lambda}}_{T}=f(\tilde{x}/\mathit{Gz})$
.
$\tilde{{\it\lambda}}_{T}=f(\tilde{x}/\mathit{Gz})$
.
2.5. Numerical procedure
Numerically, the Graetz–Nusselt problem for finite slip was solved using the pdepe solver in matlab (MathWorks). The relative and absolute tolerances for the pdepe solver were set at
![]() $10^{-6}$
and
$10^{-6}$
and
![]() $10^{-12}$
respectively. To calculate
$10^{-12}$
respectively. To calculate
![]() $\partial _{\tilde{r}}{\rm\Theta}$
at
$\partial _{\tilde{r}}{\rm\Theta}$
at
![]() $\tilde{r}=1$
the matlab function pdeval was utilised.
$\tilde{r}=1$
the matlab function pdeval was utilised.
Because heat transport mainly occurs near the inlet and near the wall, the
![]() $\tilde{x}\times \tilde{r}=82\times 101$
mesh was refined near these boundaries. The exponent
$\tilde{x}\times \tilde{r}=82\times 101$
mesh was refined near these boundaries. The exponent
![]() ${\it\beta}$
was evaluated in two distinct manners. The fitting of a straight line through
${\it\beta}$
was evaluated in two distinct manners. The fitting of a straight line through
![]() $\log _{10}(\mathit{Nu}_{x})$
for
$\log _{10}(\mathit{Nu}_{x})$
for
![]() $-7\leqslant \log _{10}(\tilde{x}/\mathit{Gz})\leqslant -4$
using the polyfit algorithm gives a specific constant value for
$-7\leqslant \log _{10}(\tilde{x}/\mathit{Gz})\leqslant -4$
using the polyfit algorithm gives a specific constant value for
![]() ${\it\beta}$
for each
${\it\beta}$
for each
![]() $\tilde{b}$
, which is referred to as
$\tilde{b}$
, which is referred to as
![]() ${\it\beta}_{f}$
. The gradient of
${\it\beta}_{f}$
. The gradient of
![]() $\log _{10}(\mathit{Nu}_{x})$
or
$\log _{10}(\mathit{Nu}_{x})$
or
![]() $\log _{10}(g(X))$
to
$\log _{10}(g(X))$
to
![]() $\log _{10}(\tilde{x}/\mathit{Gz})$
, calculated by employing the second-order-accurate gradient algorithm, gives a local value for
$\log _{10}(\tilde{x}/\mathit{Gz})$
, calculated by employing the second-order-accurate gradient algorithm, gives a local value for
![]() ${\it\beta}$
for each position, which is referred to as
${\it\beta}$
for each position, which is referred to as
![]() ${\it\beta}_{l}$
. Here,
${\it\beta}_{l}$
. Here,
![]() $\mathit{Nu}_{\infty }$
is taken as the average of
$\mathit{Nu}_{\infty }$
is taken as the average of
![]() $\mathit{Nu}_{x}$
for
$\mathit{Nu}_{x}$
for
![]() $\tilde{x}/\mathit{Gz}\geqslant 0.1$
. To compute
$\tilde{x}/\mathit{Gz}\geqslant 0.1$
. To compute
![]() $\left\langle {\rm\Theta}\right\rangle$
the trapz script was utilised. The value of
$\left\langle {\rm\Theta}\right\rangle$
the trapz script was utilised. The value of
![]() $\tilde{{\it\lambda}}_{T}$
was approximated by linear interpolation using the two grid points closest to
$\tilde{{\it\lambda}}_{T}$
was approximated by linear interpolation using the two grid points closest to
![]() ${\rm\Theta}=0.99$
.
${\rm\Theta}=0.99$
.

Figure 2. (a) The local Nusselt number
![]() $\mathit{Nu}_{x}$
as a function of the position
$\mathit{Nu}_{x}$
as a function of the position
![]() $\tilde{x}/\mathit{Gz}$
for various slip lengths
$\tilde{x}/\mathit{Gz}$
for various slip lengths
![]() $\tilde{b}$
. The values of the scaling exponent
$\tilde{b}$
. The values of the scaling exponent
![]() ${\it\beta}$
and the developed Nusselt number
${\it\beta}$
and the developed Nusselt number
![]() $\mathit{Nu}_{\infty }$
for the limiting cases of no-slip (
$\mathit{Nu}_{\infty }$
for the limiting cases of no-slip (
![]() $\tilde{b}=0$
) and no-shear flow (
$\tilde{b}=0$
) and no-shear flow (
![]() $\tilde{b}=\infty$
) are also indicated. (b) The scaling exponent
$\tilde{b}=\infty$
) are also indicated. (b) The scaling exponent
![]() ${\it\beta}_{f}$
(obtained by fitting) and the developed Nusselt number
${\it\beta}_{f}$
(obtained by fitting) and the developed Nusselt number
![]() $\mathit{Nu}_{\infty }$
as a function of the slip length
$\mathit{Nu}_{\infty }$
as a function of the slip length
![]() $\tilde{b}$
. Remarkably, these two curves transition at different values of
$\tilde{b}$
. Remarkably, these two curves transition at different values of
![]() $\tilde{b}$
.
$\tilde{b}$
.
3. Results and discussion
3.1. Nusselt profiles
In figure 2(a) the Nusselt profiles are displayed for a wide range of slip lengths
![]() $\tilde{b}$
. The profiles reveal that for
$\tilde{b}$
. The profiles reveal that for
![]() $\tilde{b}<10^{-4}$
the classical Graetz–Nusselt solution for no-slip flow is approached, with
$\tilde{b}<10^{-4}$
the classical Graetz–Nusselt solution for no-slip flow is approached, with
![]() ${\it\beta}=1/3$
. For
${\it\beta}=1/3$
. For
![]() $\tilde{b}>10^{2}$
the classical solution for no-shear flow is recovered, for which
$\tilde{b}>10^{2}$
the classical solution for no-shear flow is recovered, for which
![]() ${\it\beta}=1/2$
. For intermediate values of
${\it\beta}=1/2$
. For intermediate values of
![]() $\tilde{b}$
, the figure shows that first the exponent
$\tilde{b}$
, the figure shows that first the exponent
![]() ${\it\beta}$
(the slope) starts to change value, followed by an increase of
${\it\beta}$
(the slope) starts to change value, followed by an increase of
![]() $\mathit{Nu}_{\infty }$
.
$\mathit{Nu}_{\infty }$
.
The dependence of
![]() ${\it\beta}_{f}$
and
${\it\beta}_{f}$
and
![]() $\mathit{Nu}_{\infty }$
on the slip length
$\mathit{Nu}_{\infty }$
on the slip length
![]() $\tilde{b}$
is shown in figure 2(b). This figure illustrates that the transition points for
$\tilde{b}$
is shown in figure 2(b). This figure illustrates that the transition points for
![]() ${\it\beta}_{f}$
and
${\it\beta}_{f}$
and
![]() $\mathit{Nu}_{\infty }$
are located more than one order of magnitude apart. The exponent
$\mathit{Nu}_{\infty }$
are located more than one order of magnitude apart. The exponent
![]() ${\it\beta}_{f}$
changes value when
${\it\beta}_{f}$
changes value when
![]() $10^{-4}<\tilde{b}<10^{0}$
, while
$10^{-4}<\tilde{b}<10^{0}$
, while
![]() $\mathit{Nu}_{\infty }$
gradually increases from 3.66 to 5.78 when
$\mathit{Nu}_{\infty }$
gradually increases from 3.66 to 5.78 when
![]() $10^{-2}<\tilde{b}<10^{2}$
. This corresponds to the values for
$10^{-2}<\tilde{b}<10^{2}$
. This corresponds to the values for
![]() $\mathit{Nu}_{\infty }$
found by Barron et al. (Reference Barron, Wang, Ameel and Warrington1997), who solved the Graetz–Nusselt problem in the thermally developed regime for
$\mathit{Nu}_{\infty }$
found by Barron et al. (Reference Barron, Wang, Ameel and Warrington1997), who solved the Graetz–Nusselt problem in the thermally developed regime for
![]() $0\leqslant \tilde{b}\leqslant 0.24$
(Ezquerra Larrodé et al.
Reference Ezquerra Larrodé, Housiadas and Drossinos2000). It should be noted that a change in the range of
$0\leqslant \tilde{b}\leqslant 0.24$
(Ezquerra Larrodé et al.
Reference Ezquerra Larrodé, Housiadas and Drossinos2000). It should be noted that a change in the range of
![]() $\tilde{x}/\mathit{Gz}$
values used to compute
$\tilde{x}/\mathit{Gz}$
values used to compute
![]() ${\it\beta}_{f}$
results in a different transition point for
${\it\beta}_{f}$
results in a different transition point for
![]() ${\it\beta}_{f}$
. The use of larger values shifts the transition point upwards. Nonetheless, the distance between the transition points for
${\it\beta}_{f}$
. The use of larger values shifts the transition point upwards. Nonetheless, the distance between the transition points for
![]() ${\it\beta}_{f}$
and
${\it\beta}_{f}$
and
![]() $\mathit{Nu}_{\infty }$
remains of at least one order of magnitude.
$\mathit{Nu}_{\infty }$
remains of at least one order of magnitude.
The exponent
![]() ${\it\beta}$
is not necessarily a specific constant value for finite slip as it is for no-slip and no-shear flow. Therefore, the local exponent
${\it\beta}$
is not necessarily a specific constant value for finite slip as it is for no-slip and no-shear flow. Therefore, the local exponent
![]() ${\it\beta}_{l}$
was evaluated both numerically and analytically. In figure 3(a),
${\it\beta}_{l}$
was evaluated both numerically and analytically. In figure 3(a),
![]() ${\it\beta}_{l}$
is plotted versus
${\it\beta}_{l}$
is plotted versus
![]() $\tilde{x}/\mathit{Gz}$
for various slip lengths
$\tilde{x}/\mathit{Gz}$
for various slip lengths
![]() $\tilde{b}$
. The profiles confirm that for approximately
$\tilde{b}$
. The profiles confirm that for approximately
![]() $10^{-4}<\tilde{b}<10^{0}$
,
$10^{-4}<\tilde{b}<10^{0}$
,
![]() ${\it\beta}_{l}$
is not constant and depends on both the position and the slip length. Furthermore, we observe that
${\it\beta}_{l}$
is not constant and depends on both the position and the slip length. Furthermore, we observe that
![]() ${\it\beta}_{l}$
always transitions from
${\it\beta}_{l}$
always transitions from
![]() $1/2$
to
$1/2$
to
![]() $1/3$
, except for the limits
$1/3$
, except for the limits
![]() $\tilde{b}=0$
and
$\tilde{b}=0$
and
![]() $\tilde{b}=\infty$
.
$\tilde{b}=\infty$
.
The numerical and analytical results are in good agreement, but start to deviate when
![]() $\tilde{x}/\mathit{Gz}>10^{-5}$
. In that case the thermal and viscous boundary layer thicknesses are of the same order of magnitude (
$\tilde{x}/\mathit{Gz}>10^{-5}$
. In that case the thermal and viscous boundary layer thicknesses are of the same order of magnitude (
![]() $\tilde{{\it\lambda}}_{T}\approx 0.1$
for
$\tilde{{\it\lambda}}_{T}\approx 0.1$
for
![]() $\tilde{x}/\mathit{Gz}=10^{-4}$
). Consequently, the assumptions arising from the Lévêque approximation, and therefore also the analytical results, are no longer entirely valid.
$\tilde{x}/\mathit{Gz}=10^{-4}$
). Consequently, the assumptions arising from the Lévêque approximation, and therefore also the analytical results, are no longer entirely valid.
3.2. On
 ${\it\beta}$
and its transition point
${\it\beta}$
and its transition point
That
![]() ${\it\beta}_{l}$
must transition from
${\it\beta}_{l}$
must transition from
![]() $1/2$
to
$1/2$
to
![]() $1/3$
, except for
$1/3$
, except for
![]() $\tilde{b}=0$
and
$\tilde{b}=0$
and
![]() $\tilde{b}=\infty$
, can be demonstrated by inspection of the function
$\tilde{b}=\infty$
, can be demonstrated by inspection of the function
![]() $g(X)$
. First, as figure 3(b) reveals, the classical limits are recovered by this function, as
$g(X)$
. First, as figure 3(b) reveals, the classical limits are recovered by this function, as
![]() $\mathit{Nu}_{x}\propto g(X)$
. When
$\mathit{Nu}_{x}\propto g(X)$
. When
![]() $\tilde{b}\rightarrow 0$
, we would expect that
$\tilde{b}\rightarrow 0$
, we would expect that
![]() $g(X)\propto X^{-1/3}$
for
$g(X)\propto X^{-1/3}$
for
![]() $X\rightarrow \infty$
. Thus,
$X\rightarrow \infty$
. Thus,
When
![]() $\tilde{b}\rightarrow \infty$
, we would expect that for
$\tilde{b}\rightarrow \infty$
, we would expect that for
![]() $X\rightarrow 0$
,
$X\rightarrow 0$
,
![]() $g(X)\propto X^{-1/2}$
. Then,
$g(X)\propto X^{-1/2}$
. Then,
Second, for each value of
![]() $0<\tilde{b}<\infty$
we can choose
$0<\tilde{b}<\infty$
we can choose
![]() $\tilde{x}$
such that
$\tilde{x}$
such that
![]() $X\rightarrow 0$
. As in that case (3.2) is recovered, we find that for finite slip
$X\rightarrow 0$
. As in that case (3.2) is recovered, we find that for finite slip
![]() ${\it\beta}_{l}$
always transitions from
${\it\beta}_{l}$
always transitions from
![]() $1/2$
to
$1/2$
to
![]() $1/3$
. Consequently, it can be concluded that for a given slip length
$1/3$
. Consequently, it can be concluded that for a given slip length
![]() $\tilde{b}$
, the Nusselt profile in the thermally developing regime cannot be characterised by a single
$\tilde{b}$
, the Nusselt profile in the thermally developing regime cannot be characterised by a single
![]() ${\it\beta}_{f}$
value. The range of
${\it\beta}_{f}$
value. The range of
![]() $\tilde{x}/\mathit{Gz}$
values used for computing
$\tilde{x}/\mathit{Gz}$
values used for computing
![]() ${\it\beta}_{f}$
is determinant for the value of
${\it\beta}_{f}$
is determinant for the value of
![]() ${\it\beta}_{f}$
that is obtained. Nevertheless, comparison of figures 2(b) and 3(a) shows that
${\it\beta}_{f}$
that is obtained. Nevertheless, comparison of figures 2(b) and 3(a) shows that
![]() ${\it\beta}_{f}$
does reflect for what range of slip lengths
${\it\beta}_{f}$
does reflect for what range of slip lengths
![]() $\tilde{b}$
the exponent
$\tilde{b}$
the exponent
![]() ${\it\beta}$
changes value. Finally, since
${\it\beta}$
changes value. Finally, since
![]() ${\it\beta}_{l}\approx 5/12$
when
${\it\beta}_{l}\approx 5/12$
when
![]() $X=1$
, the dimensionless number
$X=1$
, the dimensionless number
![]() $X=(\tilde{x}/\mathit{Gz})(1+4\tilde{b})/\tilde{b}^{3}$
can be considered as a kind of criterion for the behaviour of
$X=(\tilde{x}/\mathit{Gz})(1+4\tilde{b})/\tilde{b}^{3}$
can be considered as a kind of criterion for the behaviour of
![]() ${\it\beta}$
:
${\it\beta}$
:
![]() ${\it\beta}\rightarrow 1/2$
when
${\it\beta}\rightarrow 1/2$
when
![]() $X\ll 1$
, whereas
$X\ll 1$
, whereas
![]() ${\it\beta}\rightarrow 1/3$
when
${\it\beta}\rightarrow 1/3$
when
![]() $X\gg 1$
.
$X\gg 1$
.

Figure 3. (a) The local scaling exponent
![]() ${\it\beta}_{l}$
versus the position
${\it\beta}_{l}$
versus the position
![]() $\tilde{x}/\mathit{Gz}$
for various slip lengths
$\tilde{x}/\mathit{Gz}$
for various slip lengths
![]() $\tilde{b}$
. (b) The limiting behaviour of
$\tilde{b}$
. (b) The limiting behaviour of
![]() $g(X)$
, from which
$g(X)$
, from which
![]() ${\it\beta}_{l}$
can be obtained analytically, is as expected:
${\it\beta}_{l}$
can be obtained analytically, is as expected:
![]() $g(X)\propto X^{-1/2}$
when
$g(X)\propto X^{-1/2}$
when
![]() $X\rightarrow 0$
, and
$X\rightarrow 0$
, and
![]() $g(X)\propto X^{-1/3}$
when
$g(X)\propto X^{-1/3}$
when
![]() $X\rightarrow \infty$
.
$X\rightarrow \infty$
.
Physically, the location of the transition regime for
![]() ${\it\beta}_{l}$
can be explained by considering the thickness of the thermal and viscous boundary layers. This is illustrated in figure 4(a). All heat transport takes place in the thermal boundary layer, where the temperature gradient at the wall,
${\it\beta}_{l}$
can be explained by considering the thickness of the thermal and viscous boundary layers. This is illustrated in figure 4(a). All heat transport takes place in the thermal boundary layer, where the temperature gradient at the wall,
![]() $\left.\partial _{\tilde{r}}{\rm\Theta}\right|_{\tilde{r}=1}$
, is most important. When the velocity in the thermal boundary layer, which is growing with
$\left.\partial _{\tilde{r}}{\rm\Theta}\right|_{\tilde{r}=1}$
, is most important. When the velocity in the thermal boundary layer, which is growing with
![]() $\tilde{x}$
, is dominated by the slip velocity
$\tilde{x}$
, is dominated by the slip velocity
![]() $\tilde{u} _{s}$
,
$\tilde{u} _{s}$
,
![]() ${\it\beta}_{l}\rightarrow 1/2$
. In that case, the velocity profile in the thermal boundary layer is approximately uniform, and thereby resembles a no-shear flow. Then, the left-hand side of (2.5) can be approximated as
${\it\beta}_{l}\rightarrow 1/2$
. In that case, the velocity profile in the thermal boundary layer is approximately uniform, and thereby resembles a no-shear flow. Then, the left-hand side of (2.5) can be approximated as
![]() $u\partial _{x}T=u_{v}\partial _{x}T+u_{s}\partial _{x}T\approx u_{s}\partial _{x}T$
. On the other hand, when the velocity in the thermal boundary layer is dominated by the parabolic velocity component
$u\partial _{x}T=u_{v}\partial _{x}T+u_{s}\partial _{x}T\approx u_{s}\partial _{x}T$
. On the other hand, when the velocity in the thermal boundary layer is dominated by the parabolic velocity component
![]() $\tilde{u} _{v}$
,
$\tilde{u} _{v}$
,
![]() ${\it\beta}_{l}\rightarrow 1/3$
. The flow profile in the thermal boundary layer resembles a no-slip flow, i.e.
${\it\beta}_{l}\rightarrow 1/3$
. The flow profile in the thermal boundary layer resembles a no-slip flow, i.e.
![]() $u\partial _{x}T\approx u_{v}\partial _{x}T$
, for which
$u\partial _{x}T\approx u_{v}\partial _{x}T$
, for which
![]() ${\it\beta}=1/3$
.
${\it\beta}=1/3$
.
The location where
![]() ${\it\beta}_{l}$
transitions from
${\it\beta}_{l}$
transitions from
![]() $1/2$
to
$1/2$
to
![]() $1/3$
can be predicted. In the thermal boundary layer, the slip velocity
$1/3$
can be predicted. In the thermal boundary layer, the slip velocity
![]() $\tilde{u} _{s}$
is dominating (i.e.
$\tilde{u} _{s}$
is dominating (i.e.
![]() $\tilde{u} _{v}\ll \tilde{u} _{s}$
) until the point
$\tilde{u} _{v}\ll \tilde{u} _{s}$
) until the point
![]() $(\tilde{x}/\mathit{Gz})_{1/2}$
. This location is estimated by calculating where
$(\tilde{x}/\mathit{Gz})_{1/2}$
. This location is estimated by calculating where
![]() $\tilde{{\it\lambda}}_{T}=\tilde{{\it\delta}}_{{\it\nu}}(\tilde{u} _{v}=0.1\tilde{u} _{s})$
. The parabolic velocity component starts to dominate in the thermal boundary layer (i.e.
$\tilde{{\it\lambda}}_{T}=\tilde{{\it\delta}}_{{\it\nu}}(\tilde{u} _{v}=0.1\tilde{u} _{s})$
. The parabolic velocity component starts to dominate in the thermal boundary layer (i.e.
![]() $\tilde{u} _{v}\gg \tilde{u} _{s}$
) from the point
$\tilde{u} _{v}\gg \tilde{u} _{s}$
) from the point
![]() $(\tilde{x}/\mathit{Gz})_{1/3}$
on. The point where
$(\tilde{x}/\mathit{Gz})_{1/3}$
on. The point where
![]() $\tilde{{\it\lambda}}_{T}=\tilde{{\it\delta}}_{{\it\nu}}(\tilde{u} _{v}=10\tilde{u} _{s})$
roughly corresponds to this location. This implies that the transition regime for
$\tilde{{\it\lambda}}_{T}=\tilde{{\it\delta}}_{{\it\nu}}(\tilde{u} _{v}=10\tilde{u} _{s})$
roughly corresponds to this location. This implies that the transition regime for
![]() ${\it\beta}_{l}$
is located between
${\it\beta}_{l}$
is located between
![]() $(\tilde{x}/\mathit{Gz})_{1/2}$
and
$(\tilde{x}/\mathit{Gz})_{1/2}$
and
![]() $(\tilde{x}/\mathit{Gz})_{1/3}$
. The locations of
$(\tilde{x}/\mathit{Gz})_{1/3}$
. The locations of
![]() $(\tilde{x}/\mathit{Gz})_{1/2}$
and
$(\tilde{x}/\mathit{Gz})_{1/2}$
and
![]() $(\tilde{x}/\mathit{Gz})_{1/3}$
are given in figure 4(b). As an example, for
$(\tilde{x}/\mathit{Gz})_{1/3}$
are given in figure 4(b). As an example, for
![]() $\tilde{b}=10^{-1}$
we find that
$\tilde{b}=10^{-1}$
we find that
![]() $(\tilde{x}/\mathit{Gz})_{1/2}=5\times 10^{-7}$
. This is in agreement with
$(\tilde{x}/\mathit{Gz})_{1/2}=5\times 10^{-7}$
. This is in agreement with
![]() ${\it\beta}_{l}$
for
${\it\beta}_{l}$
for
![]() $\tilde{b}=10^{-1}$
in figure 3(a).
$\tilde{b}=10^{-1}$
in figure 3(a).

Figure 4. (a) The location of the transition regime for
![]() ${\it\beta}_{l}$
can be explained physically by considering
${\it\beta}_{l}$
can be explained physically by considering
![]() $\tilde{{\it\lambda}}_{T}$
and
$\tilde{{\it\lambda}}_{T}$
and
![]() $\tilde{{\it\delta}}_{{\it\nu}}$
. When the slip velocity
$\tilde{{\it\delta}}_{{\it\nu}}$
. When the slip velocity
![]() $\tilde{u} _{s}$
dominates in the thermal boundary layer, which is the case when
$\tilde{u} _{s}$
dominates in the thermal boundary layer, which is the case when
![]() $\tilde{x}/\mathit{Gz}<(\tilde{x}/\mathit{Gz})_{1/2}$
,
$\tilde{x}/\mathit{Gz}<(\tilde{x}/\mathit{Gz})_{1/2}$
,
![]() ${\it\beta}_{l}\rightarrow 1/2$
. When the velocity in the thermal boundary layer is dominated by
${\it\beta}_{l}\rightarrow 1/2$
. When the velocity in the thermal boundary layer is dominated by
![]() $\tilde{u} _{v}$
,
$\tilde{u} _{v}$
,
![]() ${\it\beta}_{l}\rightarrow 1/3$
. This is true when
${\it\beta}_{l}\rightarrow 1/3$
. This is true when
![]() $\tilde{x}/\mathit{Gz}>(\tilde{x}/\mathit{Gz})_{1/3}$
. (b) The locations of
$\tilde{x}/\mathit{Gz}>(\tilde{x}/\mathit{Gz})_{1/3}$
. (b) The locations of
![]() $(\tilde{x}/\mathit{Gz})_{1/2}$
and
$(\tilde{x}/\mathit{Gz})_{1/2}$
and
![]() $(\tilde{x}/\mathit{Gz})_{1/3}$
as a function of the slip length
$(\tilde{x}/\mathit{Gz})_{1/3}$
as a function of the slip length
![]() $\tilde{b}$
are shown here. These points are estimated by saying that
$\tilde{b}$
are shown here. These points are estimated by saying that
![]() $\tilde{u} _{v}\ll \tilde{u} _{s}$
when
$\tilde{u} _{v}\ll \tilde{u} _{s}$
when
![]() $\tilde{u} _{v}=0.1\tilde{u} _{s}$
, and that
$\tilde{u} _{v}=0.1\tilde{u} _{s}$
, and that
![]() $\tilde{u} _{v}\gg \tilde{u} _{s}$
when
$\tilde{u} _{v}\gg \tilde{u} _{s}$
when
![]() $\tilde{u} _{v}=10\tilde{u} _{s}$
.
$\tilde{u} _{v}=10\tilde{u} _{s}$
.
3.3. On
 $\mathit{Nu}_{\infty }$
and its transition point
$\mathit{Nu}_{\infty }$
and its transition point
The developed Nusselt number
![]() $\mathit{Nu}_{\infty }$
concerns heat transfer in the thermally developed regime (
$\mathit{Nu}_{\infty }$
concerns heat transfer in the thermally developed regime (
![]() $\tilde{x}/\mathit{Gz}>0.1$
). In this regime the temperature and temperature gradient at the wall are approaching zero. This implies that
$\tilde{x}/\mathit{Gz}>0.1$
). In this regime the temperature and temperature gradient at the wall are approaching zero. This implies that
![]() $\mathit{Nu}_{\infty }$
can only be enhanced by increasing advective transport near the wall, where the temperature gradients are largest. Figure 5 demonstrates that when
$\mathit{Nu}_{\infty }$
can only be enhanced by increasing advective transport near the wall, where the temperature gradients are largest. Figure 5 demonstrates that when
![]() $\tilde{u} _{s}$
starts to change significantly with
$\tilde{u} _{s}$
starts to change significantly with
![]() $\tilde{b}$
,
$\tilde{b}$
,
![]() $\mathit{Nu}_{\infty }$
also transitions from 3.66 to 5.78, the limiting values for zero and infinite slip length.
$\mathit{Nu}_{\infty }$
also transitions from 3.66 to 5.78, the limiting values for zero and infinite slip length.
Replacement of
![]() $\tilde{u} _{s}$
by the velocity gradient at the wall,
$\tilde{u} _{s}$
by the velocity gradient at the wall,
![]() $\left.\partial _{\tilde{r}}\tilde{u} \right|_{\tilde{r}=1}$
, leads to the same conclusion, however. An increase in
$\left.\partial _{\tilde{r}}\tilde{u} \right|_{\tilde{r}=1}$
, leads to the same conclusion, however. An increase in
![]() $\tilde{u} _{s}$
implies that
$\tilde{u} _{s}$
implies that
![]() $\left|\partial _{\tilde{r}}\tilde{u} \right|$
must decrease. This follows from Navier’s slip condition,
$\left|\partial _{\tilde{r}}\tilde{u} \right|$
must decrease. This follows from Navier’s slip condition,
![]() $\tilde{u} _{s}=-\tilde{b}\left.\partial _{\tilde{r}}\tilde{u} \right|_{\tilde{r}=1}$
, which shows that the slip velocity and the velocity gradient at the wall are directly related to each other via the factor
$\tilde{u} _{s}=-\tilde{b}\left.\partial _{\tilde{r}}\tilde{u} \right|_{\tilde{r}=1}$
, which shows that the slip velocity and the velocity gradient at the wall are directly related to each other via the factor
![]() $-\tilde{b}$
. Moreover, from the definitions of
$-\tilde{b}$
. Moreover, from the definitions of
![]() $\tilde{u} _{s}=4\tilde{b}/(1+4\tilde{b})$
and
$\tilde{u} _{s}=4\tilde{b}/(1+4\tilde{b})$
and
![]() $\left.\partial _{\tilde{r}}\tilde{u} \right|_{\tilde{r}=1}=-4/(1+4\tilde{b})$
, we find that they have the same transition point, which is
$\left.\partial _{\tilde{r}}\tilde{u} \right|_{\tilde{r}=1}=-4/(1+4\tilde{b})$
, we find that they have the same transition point, which is
![]() $\tilde{b}=1/4$
. This is close to the transition point of
$\tilde{b}=1/4$
. This is close to the transition point of
![]() $\tilde{b}=0.4$
for
$\tilde{b}=0.4$
for
![]() $\mathit{Nu}_{\infty }$
. Furthermore, their derivatives to
$\mathit{Nu}_{\infty }$
. Furthermore, their derivatives to
![]() $\tilde{b}$
,
$\tilde{b}$
,
![]() $\partial _{\tilde{b}}\tilde{u} _{s}$
and
$\partial _{\tilde{b}}\tilde{u} _{s}$
and
![]() $\left.\partial _{\tilde{b}}(\partial _{\tilde{r}}\tilde{u} )\right|_{\tilde{r}=1}$
, are both proportional to
$\left.\partial _{\tilde{b}}(\partial _{\tilde{r}}\tilde{u} )\right|_{\tilde{r}=1}$
, are both proportional to
![]() $(1+4\tilde{b})^{-2}$
.
$(1+4\tilde{b})^{-2}$
.
Therefore, the change of neither
![]() $\tilde{u} _{s}$
nor
$\tilde{u} _{s}$
nor
![]() $\left.\partial _{\tilde{r}}\tilde{u} \right|_{\tilde{r}=1}$
with slip length
$\left.\partial _{\tilde{r}}\tilde{u} \right|_{\tilde{r}=1}$
with slip length
![]() $\tilde{b}$
fully explains the dependence of
$\tilde{b}$
fully explains the dependence of
![]() $\mathit{Nu}_{\infty }$
on
$\mathit{Nu}_{\infty }$
on
![]() $\tilde{b}$
. It is the relation between the velocity distribution and the slip length
$\tilde{b}$
. It is the relation between the velocity distribution and the slip length
![]() $\tilde{b}$
that explains how
$\tilde{b}$
that explains how
![]() $\mathit{Nu}_{\infty }$
depends on
$\mathit{Nu}_{\infty }$
depends on
![]() $\tilde{b}$
. Nevertheless, because heat transport is largest when temperature gradients are maximum, the change of
$\tilde{b}$
. Nevertheless, because heat transport is largest when temperature gradients are maximum, the change of
![]() $\tilde{u} _{s}$
with
$\tilde{u} _{s}$
with
![]() $\tilde{b}$
most dominantly affects the behaviour of
$\tilde{b}$
most dominantly affects the behaviour of
![]() $\mathit{Nu}_{\infty }$
. This is in agreement with the observation of Barrow & Humphreys (Reference Barrow and Humphreys1970) that, given an average fluid velocity, increase of the velocity at the wall leads to larger Nusselt numbers.
$\mathit{Nu}_{\infty }$
. This is in agreement with the observation of Barrow & Humphreys (Reference Barrow and Humphreys1970) that, given an average fluid velocity, increase of the velocity at the wall leads to larger Nusselt numbers.

Figure 5. The developed Nusselt number
![]() $\mathit{Nu}_{\infty }$
and slip velocity
$\mathit{Nu}_{\infty }$
and slip velocity
![]() $\tilde{u} _{s}$
versus the slip length
$\tilde{u} _{s}$
versus the slip length
![]() $\tilde{b}$
.
$\tilde{b}$
.
3.4. Employing wall slip to increase heat transfer
The Nusselt profiles in figure 2(a) suggest that heat transport can be optimised by employing wall slip, provided that the wall slip is large enough. Partial slip lengths are usually of the order of tens of nanometres for microscale systems (Rothstein Reference Rothstein2010). As a consequence, the maximum tube radius is approximately
![]() $1~{\rm\mu}\text{m}$
for
$1~{\rm\mu}\text{m}$
for
![]() ${\it\beta}$
to be significantly larger than
${\it\beta}$
to be significantly larger than
![]() $1/3$
. For
$1/3$
. For
![]() $\mathit{Nu}_{\infty }$
to be larger than 3.66, tube radii should be of the order of nanometres. However, the Graetz number is usually very small. For a typical liquid like water,
$\mathit{Nu}_{\infty }$
to be larger than 3.66, tube radii should be of the order of nanometres. However, the Graetz number is usually very small. For a typical liquid like water,
![]() $\mathit{Re}\sim 1$
and
$\mathit{Re}\sim 1$
and
![]() $\mathit{Pr}\sim 1$
. For both micro- and nanofluidics it is estimated that
$\mathit{Pr}\sim 1$
. For both micro- and nanofluidics it is estimated that
![]() $D/L<10^{-3}$
, implying that
$D/L<10^{-3}$
, implying that
![]() $\mathit{Gz}<10^{-3}$
. In that case, the temperature profile is almost instantaneously thermally developed, as this is then true for
$\mathit{Gz}<10^{-3}$
. In that case, the temperature profile is almost instantaneously thermally developed, as this is then true for
![]() $\tilde{x}\,>10^{-4}$
.
$\tilde{x}\,>10^{-4}$
.
Thus, enhancement of heat transfer by employing finite slip, while avoiding reaching the thermally developed regime, is possible if two conditions are met. First, the system should be designed such that
![]() $\mathit{Gz}>1$
. Second, the slip length should be of the order of the tube radius, i.e.
$\mathit{Gz}>1$
. Second, the slip length should be of the order of the tube radius, i.e.
![]() $\tilde{b}\sim 1$
. These conditions oppose one another. In nanofluidic systems, slip lengths
$\tilde{b}\sim 1$
. These conditions oppose one another. In nanofluidic systems, slip lengths
![]() $\tilde{b}$
of approximately
$\tilde{b}$
of approximately
![]() $10^{3}$
can be obtained (Whitby & Quirke Reference Whitby and Quirke2007; Majumder et al.
Reference Majumder, Chopra and Hinds2011). This implies that
$10^{3}$
can be obtained (Whitby & Quirke Reference Whitby and Quirke2007; Majumder et al.
Reference Majumder, Chopra and Hinds2011). This implies that
![]() $\tilde{b}$
is large enough to let
$\tilde{b}$
is large enough to let
![]() $\mathit{Nu}_{\infty }\rightarrow 5.78$
, albeit the thermally developing section is negligibly small. Additionally, for instance, highly slippery liquid-infused porous surfaces (Lafuma & Quéré Reference Lafuma and Quéré2011; Wong et al.
Reference Wong, Kang, Tang, Smythe, Hatton, Grinthal and Aizenberg2011) could be exploited to enhance heat transport.
$\mathit{Nu}_{\infty }\rightarrow 5.78$
, albeit the thermally developing section is negligibly small. Additionally, for instance, highly slippery liquid-infused porous surfaces (Lafuma & Quéré Reference Lafuma and Quéré2011; Wong et al.
Reference Wong, Kang, Tang, Smythe, Hatton, Grinthal and Aizenberg2011) could be exploited to enhance heat transport.
It should be noted that the results presented here are applicable to systems that display homogeneous wall slip. Distinct results are expected for systems concerning effective slip (Maynes, Webb & Davies Reference Maynes, Webb and Davies2008; Maynes et al. Reference Maynes, Webb, Crockett and Solovjov2012; Enright et al. Reference Enright, Hodes, Salamon and Muzychka2013). As such, the Graetz–Nusselt problem for heterogeneously slippery surfaces deserves to be studied separately.
4. Conclusion
This study provides numerical and analytical solutions to the Graetz–Nusselt problem for continuum flows with finite slip. The classical solutions to this problem concern no-slip and no-shear flow. These form the lower and upper limits of the solutions for partial slip, as the resulting Nusselt profiles gradually transition between these limits on increasing the wall slip from zero to infinity.
The heat transfer mechanism in the thermally developing regime depends on the velocity profile in the thermal boundary layer, and is a function of wall slip and position. The ratio of the parabolic velocity component to the slip velocity determines whether it resembles the transport mechanism for no-slip or for no-shear flow. The Nusselt number in the thermally developed regime depends on the fluid velocity profile only.
By considering slip lengths ranging from zero to infinity, this study is the first to connect the classical solutions to the Graetz–Nusselt problem. This is not only of fundamental interest, but also makes it possible to evaluate the influence of wall slip on heat transfer in many forced convection problems in science and engineering.
Acknowledgements
R.G.H.L. acknowledges the European Research Council for the ERC starting grant 307342-TRAM. D.L. acknowledges an ERC advanced grant.
Supplementary data
Supplementary data is available at http://dx.doi.org/10.1017/jfm.2014.733.