Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Nagata, R.
Watanabe, T.
and
Nagata, K.
2018.
Turbulent/non-turbulent interfaces in temporally evolving compressible planar jets.
Physics of Fluids,
Vol. 30,
Issue. 10,
Zhang, Xinxian
Watanabe, Tomoaki
and
Nagata, Koji
2019.
Passive scalar mixing near turbulent/non-turbulent interface in compressible turbulent boundary layers.
Physica Scripta,
Vol. 94,
Issue. 4,
p.
044002.
Zhuang, Yi
Tan, Huijun
Wang, Weixing
Li, Xin
and
Guo, Yunjie
2019.
Fractal features of turbulent/non-turbulent interface in a shock wave/turbulent boundary-layer interaction flow.
Journal of Fluid Mechanics,
Vol. 869,
Issue. ,
Ma, Kai
Li, Jiang
Li, Qiang
and
Liu, Yang
2020.
Experimental study on evolution characteristics of plane subsonic-supersonic shear layer.
Aerospace Science and Technology,
Vol. 100,
Issue. ,
p.
105791.
Kohan, Khashayar F.
and
Gaskin, Susan
2020.
The effect of the geometric features of the turbulent/non-turbulent interface on the entrainment of a passive scalar into a jet.
Physics of Fluids,
Vol. 32,
Issue. 9,
Zhang, Xinxian
2021.
Frontiers of Digital Transformation.
p.
155.
Gang, Dundian
Yi, Shi-he
and
Niu, Haibo
2021.
Visualization of supersonic flow over a rotating blunt cylinder at a high angle of attack.
Journal of Visualization,
Vol. 24,
Issue. 6,
p.
1123.
Ghasemi, Abbas
Yun, Sangsig
and
Li, Xianguo
2021.
Fractal structures arising from interfacial instabilities in bio-oil atomization.
Scientific Reports,
Vol. 11,
Issue. 1,
GANG, Dundian
YI, Shihe
ZHANG, Feng
and
NIU, Haibo
2022.
Effects of sweep angles on turbulent separation behaviors induced by blunt fin.
Chinese Journal of Aeronautics,
Vol. 35,
Issue. 3,
p.
90.
Tang, M.X.
Wu, Y.
Zong, H.H.
Luo, Y.H.
Yang, H.S.
and
Guo, S.G.
2022.
Experimental investigation of supersonic boundary-layer tripping with a spanwise pulsed spark discharge array.
Journal of Fluid Mechanics,
Vol. 931,
Issue. ,
Zhang, Xinxian
Watanabe, Tomoaki
and
Nagata, Koji
2023.
Reynolds number dependence of the turbulent/non-turbulent interface in temporally developing turbulent boundary layers.
Journal of Fluid Mechanics,
Vol. 964,
Issue. ,
Huang, Jianda
and
Bai, Honglei
2024.
Turbulent/non-turbulent interface of the turbulent boundary-layer over a spanwise-heterogeneous converging/diverging riblets rough wall.
Fluid Dynamics Research,
Vol. 56,
Issue. 2,
p.
025503.
Liu, Xiaolin
and
Yi, Shihe
2024.
Experimental investigation about the aerodynamic noise caused by hypersonic turbulence.
Physics of Fluids,
Vol. 36,
Issue. 1,
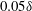 $0.05\unicode[STIX]{x1D6FF}$.
$0.05\unicode[STIX]{x1D6FF}$.



