The dynamics of an axisymmetric liquid bridge of a fluid of density 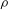${\it\rho}$, viscosity 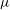${\it\mu}$ and surface tension ${\it\sigma}$ held between two co-axial disks of equal radius $e$ is studied when one disk is slowly moved with a velocity 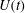$U(t)$. The analysis is performed using a one-dimensional model for thin bridges. We consider attached boundary conditions (the contact line is fixed to the boundary of the disk), neglect gravity and limit our analysis to short bridges such that there exists a stable equilibrium shape. This equilibrium is a Delaunay curve characterized by the two geometric parameters 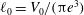$\ell _{0}=V_{0}/({\rm\pi}e^{3})$ and 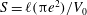$S=\ell ({\rm\pi}e^{2})/V_{0}$, where $V_{0}$ is the volume of fluid and 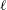$\ell$ the length of the bridge. Our objective is to analyse the departure of the dynamical solution from the static Delaunay shape as a function of 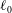$\ell _{0}$, 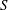$S$, the Ohnesorge number 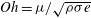$Oh={\it\mu}/\sqrt{{\it\rho}{\it\sigma}e}$, and the instantaneous velocity 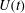$U(t)$ and acceleration 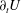$\partial _{t}U$ (non-dimensionalized using $e$ and 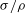${\it\sigma}/{\it\rho}$) of the disk. Using a perturbation theory for small velocity and acceleration, we show that (i) a non-homogeneous velocity field proportional to 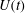$U(t)$ and independent of 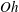$Oh$ is present within the bridge; (ii) the area correction to the equilibrium shape can be written as $U^{2}A_{i}+U\,Oh\,A_{v}+\partial _{t}UA_{a}$ where 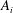$A_{i}$, 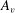$A_{v}$ and 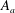$A_{a}$ are functions of 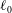$\ell _{0}$ and 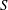$S$ only. The characteristics of the velocity field and the shape corrections are analysed in detail. For the case of a cylinder (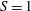$S=1$), explicit expressions are derived and used to provide some insight into the break-up that the deformation would induce. The asymptotic results are validated and tested by direct numerical simulations when the velocity is constant and when it oscillates. For the constant velocity case, we demonstrate that the theory provides a very good estimate of the dynamics for a large range of parameters. However, a systematic departure is observed for very small $Oh$ due to the persistence of free eigenmodes excited during the transient. These same eigenmodes also limit the applicability of the theory to oscillating bridges with large oscillating periods. Finally, the perturbation theory is applied to the cylindrical solution of Frankel & Weihs (J. Fluid Mech., vol. 155 (1985), pp. 289–307) obtained for constant velocity 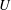$U$ when the contact lines are allowed to move. We show that it can be used to compute the correction associated with acceleration. Finally, the effect of gravity is discussed and shown to modify the equilibrium shape but not the main results obtained from the perturbation theory.