Hostname: page-component-84b7d79bbc-4hvwz Total loading time: 0 Render date: 2024-07-28T23:32:24.786Z Has data issue: false hasContentIssue false
  • English
  • Français

Flows in annuli with longitudinal grooves

Published online by Cambridge University Press:  25 January 2013

H. V. Moradi  and
J. M. Floryan
H. V. Moradi*
Affiliation:
Department of Mechanical and Materials Engineering, The University of Western Ontario, London, Ontario N6A 5B9, Canada
J. M. Floryan
Affiliation:
Department of Mechanical and Materials Engineering, The University of Western Ontario, London, Ontario N6A 5B9, Canada
*
†Email address for correspondence: hvafadar@uwo.ca
Get access Rights & Permissions [Opens in a new window]

Abstract

Analysis of pressure losses in laminar flows through annuli fitted with longitudinal grooves has been carried out. The additional pressure gradient required in order to maintain the same flow rate in the grooved annuli, as well as in the reference smooth annuli, is used as a measure of the loss. The groove-induced changes can be represented as a superposition of a pressure drop due to a change in the average position of the bounding cylinders and a pressure drop due to flow modulations induced by the shape of the grooves. The former effect can be evaluated analytically while the latter requires explicit computations. It has been demonstrated that a reduced-order model is an effective tool for extraction of the features of groove geometry that lead to flow modulations relevant to drag generation. One Fourier mode from the Fourier expansion representing the annulus geometry is sufficient to predict pressure losses with an accuracy sufficient for most applications in the case of equal-depth grooves. It is shown that the presence of the grooves may lead to a reduction of pressure loss in spite of an increase of the surface wetted area. The drag-decreasing grooves are characterized by the groove wavenumber $M/ {R}_{1} $ being smaller than a certain critical value, where 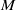$M$ denotes the number of grooves and 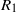${R}_{1} $ stands for the radius of the annulus. This number marginally depends on the groove amplitude and does not depend on the flow Reynolds number. It is shown that the drag reduction mechanism relies on the re-arrangement of the bulk flow that leads to the largest mass flow taking place in the area of the largest annulus opening. The form of the optimal grooves from the point of view of the maximum drag reduction has been determined. This form depends on the type of constraints imposed. In general, the optimal shape can be described using the reduced-order model involving only a few Fourier modes. It is shown that in the case of equal-depth grooves, the optimal shape can be approximated using a special form of trapezoid. In the case of unequal-depth grooves, where the groove depth needs to be determined as part of the optimization procedure, the optimal geometry, consisting of the optimal depth and the corresponding optimal shape, can be approximated using a delta function. The maximum possible drag reduction, corresponding to the optimal geometry, has been determined.

JFM classification

Flow Control: Drag reduction Flow Control: Flow Control
Type
Papers
Information
Journal of Fluid Mechanics , Volume 716 , 10 February 2013 , pp. 280 - 315
Copyright
©2013 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Asai, M. & Floryan, J. M. 2006 Experiments on the linear instability of flow in a wavy channel. Eur. J. Mech. (B/Fluids) 25, 971–986.Google Scholar
Bechert, D. W. & Bartenwerfer, M. 1989 The viscous flow on surfaces with longitudinal ribs. J. Fluid Mech. 206, 105–129.Google Scholar
Bechert, D. W., Bruse, M., Hage, W., Van Der Hoeven, J. G. T. & Hoppe, G. 1997 Experiments on drag-reducing surfaces and their optimization with an adjustable geometry. J. Fluid Mech. 338, 59–87.Google Scholar
Coleman, T. F. & Li, Y. 1994 On the convergence of reflective Newton method for large-scale nonlinear minimization subject to bounds. Math. Prog. 67, 189–224.CrossRefGoogle Scholar
Coleman, T. F. & Li, Y. 1996 An interior, trust region approach to nonlinear minimization subject to bounds. SIAM J. Optim. 6, 418–445.Google Scholar
Cotrell, D. L. & Pearlstein, A. L. 2006 Linear stability of spiral and annular Poiseuille flow for small radius ratio. J. Fluid Mech. 547, 1–20.Google Scholar
Darcy, H. 1857 Recherches Expérimentales Relatives au Mouvement de l’Eau dans les Tuyaux. Mallet-Bachelier.Google Scholar
Dou, H.-S. 2011 Physics of flow instability and turbulent transition in shear flows. Intl J. Phys. Sci. 6 (6), 1411–1425.Google Scholar
Dou, H. S., Khoo, B. C. & Tsai, H. M. 2010 Determining the critical conditions of turbulent transition in a fully developed annulus flow. J. Petrol. Sci. Engng 73, 41–47.CrossRefGoogle Scholar
Floryan, J. M. 1997 Stability of wall-bounded shear layers in the presence of simulated distributed surface roughness. J. Fluid Mech. 335, 29–55.Google Scholar
Floryan, J. M. 2002 Centrifugal instability of Couette flow over a wavy-wall. Phys. Fluids 14, 312–322.Google Scholar
Floryan, J. M. 2003 Vortex instability in a diverging–converging channel. J. Fluid Mech. 482, 17–50.Google Scholar
Floryan, J. M. 2005 Two-dimensional instability of flow in a rough channel. Phys. Fluids 17, 044101.Google Scholar
Floryan, J. M. 2007 Three-dimensional instabilities of laminar flow in a rough channel and the concept of hydraulically smooth wall. Eur. J. Mech. (B/Fluids) 26, 305–329.Google Scholar
Floryan, J. M. & Asai, M. 2011 On the transition between distributed and isolated surface roughness and its effect on the stability of channel flow. Phys. Fluids 23, 104101.Google Scholar
Floryan, J. M. & Floryan, C. 2010 Traveling wave instability in a diverging–converging channel. Fluid Dyn. Res. 42, 025509.Google Scholar
Freai, Ch., Lüscher, P. & Wintermantel, W. 2000 Thread-annular flow in vertical pipes. J. Fluid Mech. 410, 185–210.Google Scholar
Frohnapfel, B., Jovanović, J. & Delgado, A. 2007 Experimental investigations of turbulent drag reduction by surface-embedded grooves. J. Fluid Mech. 590, 107–116.CrossRefGoogle Scholar
Gamrat, G., Favre-Marinet, M., Le Person, S., Baviére, R. & Ayela, F. 2008 An experimental study and modeling of roughness effects on laminar flow in microchannels. J. Fluid Mech. 594, 399–423.Google Scholar
Garcia-Mayoral, R. & Jimenez, J. 2011 Hydrodynamic stability and breakdown of the viscous regime over riblets. J. Fluid Mech. 678, 317–347.Google Scholar
Hagen, G. 1854 Uber den Einfluss der Temperatur auf die Bewegung des Wasser in Röhren. Math. Abh. Akad. Wiss. 17.Google Scholar
Heaton, C. J. 2008 Linear instability of annular Poiseuille flow. J. Fluid Mech. 610, 391–406.Google Scholar
Herwig, H., Gloss, D. & Wenterodt, T. 2008 A new approach to understanding and modelling the influence of wall roughness on friction factors for pipe and channel flows. J. Fluid Mech. 613, 35–53.Google Scholar
Jimenez, J. 2004 Turbulent flows over rough walls. Annu. Rev. Fluid Mech. 36, 173–196.CrossRefGoogle Scholar
Jung, Y. C. & Bhushan, B. 2010 Biomimetic structures for fluid drag reduction in laminar and turbulent flows. J. Phys.: Condens. Matter 22, 035104 1–9.Google Scholar
Lucini, P., Manzo, F. & Pozzi, A. 1991 Resistance of grooved surface to parallel flow and cross-flow. J. Fluid Mech. 228, 87–109.Google Scholar
Mohammadi, A. & Floryan, J. M. 2011 Pressure losses in grooved channels. Expert Systems in Fluid Dynamics Research Laboratory Rep. ESFD-4/2011. Department of Mechanical and Materials Engineering, The University of Western Ontario.Google Scholar
Mohammadi, A. & Floryan, J. M. 2012 Mechanism of drag generation by surface corrugation. Phys. Fluids 24, 013602.Google Scholar
Moody, L. F. & Princeton, N. J. 1944 Friction factors for pipe flow. Trans. ASME 66, 671–684.Google Scholar
Moradi, H. V. & Floryan, J. M. 2012 Algorithm for analysis of flows in ribbed annuli. Intl J. Numer. Meth. Fluids 68, 805–838.Google Scholar
Morini, G. L. 2004 Single-phase convective heat transfer in microchannels: a review of experimental results. Intl J. Therm. Sci. 43, 631–651.Google Scholar
Morkovin, M. V. 1990 On roughness-induced transition: facts, views and speculations. In Instability and Transition (ed. Hussaini, M. Y. & Voigt, R. G.). ICASE/NASA LARC Series , vol. 1, pp. 281–295. Springer.Google Scholar
Nikuradse, J. 1933 Strömungsgesetze in Rauhen Rohren. VDI-Forschungscheft 361; also NACA TM 1292 (1950).Google Scholar
Nye, J. F. 1969 A calculation on the sliding of ice over a wavy surface using a Newtonian viscous approximation. Proc. R. Soc.Lond. A 311, 445–467.Google Scholar
Papautsky, I., Brazzle, J., Ameel, T. & Frazier, A. B. 1999 Laminar fluid behavior in microchannels using micropolar fluid theory. Sensors Actuators A 73, 101–108.Google Scholar
Reynolds, O. 1883 An experimental investigation of the circumstances which determine whether the motion of water shall be direct or sinuous, and of the law of resistance in parallel channels. Phil. Trans. R. Soc. Lond. 174, 935–982.Google Scholar
Saric, W. S., Carrillo, R. B. & Reibert, M. S. 1998 Nonlinear stability and transition in 3-D boundary layers. Meccanica 33, 469–487.Google Scholar
Schlichting, H. 1979 Boundary Layer Theory, 7th edn. McGraw-Hill.Google Scholar
Sharp, K. V. & Adrian, R. J. 2004 Transition from laminar to turbulent flow in liquid filled microtubes. Exp. Fluids 36, 741–747.CrossRefGoogle Scholar
Sobhan, C. B. & Garimella, S. V. 2001 A comparative analysis of studies on heat transfer and fluid flow in microchannels. Microscale Therm. Engng 5, 293–311.Google Scholar
Szumbarski, J. & Floryan, J. M. 2006 Transient disturbance growth in a corrugated channel. J. Fluid Mech. 568, 243–272.Google Scholar
Tasos, C. P., Georgios, C. G. & Andreas, N. A. 1999 Viscous Fluid Flow. CRC.Google Scholar
Valdes, J. R., Miana, M. J., Pelegay, J. L., Nunez, J. L. & Pütz, T. 2007 Numerical investigation of the influence of roughness on the laminar incompressible fluid flow through annular microchannels. Intl J. Heat Mass Transfer 50, 1865–1878.Google Scholar
Walton, A. G., Labadin, J. & Yiong, S. P. 2010 Axial flow between sliding, non-concentric cylinders with applications to thread injection. Q. J. Mech. Appl. Maths 63, 315–334.Google Scholar
Walsh, M. J. 1980 Drag characteristics of V-groove and transverse curvature riblets. In Viscous Drag Reduction (ed. Hough, G. R.), vol. 72, pp. 168–184. AIAA.Google Scholar
Walsh, M. J. 1983 Riblets as a viscous drag reduction technique. AIAA J. 21, 485–486.CrossRefGoogle Scholar