Hostname: page-component-76fb5796d-2lccl Total loading time: 0 Render date: 2024-04-26T13:04:33.532Z Has data issue: false hasContentIssue false
  • English
  • Français

Flow-induced vibration of two cylinders in tandem and staggered arrangements

Published online by Cambridge University Press:  02 November 2017

Martin D. Griffith Open the ORCID record for Martin D. Griffith [Opens in a new window] ,
David Lo Jacono ,
John Sheridan  and
Justin S. Leontini
Martin D. Griffith
Affiliation:
Swinburne University of Technology, Hawthorn, Victoria 3122, Australia Fluids Laboratory for Aeronautical and Industrial Research (FLAIR), Department of Mechanical and Aerospace Engineering, Monash University, Melbourne, Victoria 3800, Australia
David Lo Jacono
Affiliation:
Institut de Mécanique des Fluides de Toulouse (IMFT), Université de Toulouse, CNRS, INPT, UPS, 31400 Toulouse, France
John Sheridan
Affiliation:
Fluids Laboratory for Aeronautical and Industrial Research (FLAIR), Department of Mechanical and Aerospace Engineering, Monash University, Melbourne, Victoria 3800, Australia
Justin S. Leontini
Affiliation:
Swinburne University of Technology, Hawthorn, Victoria 3122, Australia
Get access Rights & Permissions [Opens in a new window]

Abstract

A numerical study of the flow-induced vibration of two elastically mounted cylinders in tandem and staggered arrangements at Reynolds number 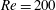$Re=200$ is presented. The cylinder centres are set at a streamwise distance of 1.5 cylinder diameters, placing the rear cylinder in the near-wake region of the front cylinder for the tandem arrangement. The cross-stream or lateral offset is varied between 0 and 5 cylinder diameters. The two cylinders are identical, with the same elastic mounting, and constrained to oscillate only in the cross-flow direction. The variation of flow behaviours is examined for static cylinders and for elastic mountings of a range of spring stiffnesses, or reduced velocity. At least seven major modes of flow response are identified, delineated by whether the oscillation is effectively symmetric, and the strength of the influence of the flow through the gap between the two cylinders. Submodes of these are also identified based on whether or not the flow remains periodic. More subtle temporal behaviours, such as period doubling, quasi-periodicity and chaos, are also identified and mapped. Across all of these regimes, the amplitudes of vibration and the magnitude of the fluid forces are quantified. The modes identified span the parameter space between two important limiting cases: two static bodies at varying lateral offset; and two elastically mounted bodies in a tandem configuration at varying spring stiffnesses. Some similarity in the response of extremely stiff or static bodies and extremely slack bodies is shown. This is explained by the fact that the slack bodies are free to move to an equilibrium position and stop, effectively becoming a static system. However, the most complex behaviour appears between these limits, when the bodies are in reasonably close proximity, and the natural structural frequency is close to the vortex shedding frequency of a single cylinder. This appears to be driven by the interplay between a series of time scales, including the vortex formation time, the advection time across the gap between the cylinders and the oscillation period of both bodies. This points out an important difference between this multi-body system and the classic single-cylinder vortex-induced vibration: two bodies in close proximity will not oscillate in a synchronised, periodic manner when their natural structural frequencies are close to the nominal vortex shedding frequency of a single cylinder.

JFM classification

Vortex Flows: Vortex shedding Wakes/Jets: Wakes/Jets
Type
Papers
Information
Journal of Fluid Mechanics , Volume 833 , 25 December 2017 , pp. 98 - 130
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alam, M. M. & Sakamoto, H. 2005 Investigation of Strouhal frequencies of two staggered bluff bodies and detection of multistable flow by wavelets. J. Fluids Struct. 20, 425–449.CrossRefGoogle Scholar
Assi, G. R. S. 2014 Wake-induced vibration of tandem and staggered cylinders with two degrees of freedom. J. Fluids Struct. 50, 340–357.CrossRefGoogle Scholar
Assi, G. R. S., Bearman, P. W. & Meneghini, J. R. 2010 On the wake-induced vibration of tandem circular cylinders: the vortex interaction excitation mechanism. J. Fluid Mech. 661, 365–401.CrossRefGoogle Scholar
Barkley, D. & Henderson, R. D. 1996 Three-dimensional Floquet stability analysis of the wake of a circular cylinder. J. Fluid Mech. 322, 215–241.CrossRefGoogle Scholar
Borazjani, I. & Sotiropoulos, F. 2009 Vortex-induced vibrations of two cylinders in tandem arrangement in the proximity-wake interference region. J. Fluid Mech. 621, 321–364.Google Scholar
Carmo, B. S., Assi, G. R. S. & Meneghini, J. R. 2013 Computational simulation of the flow-induced vibration of a circular cylinder subjected to wake interference. J. Fluids Struct. 41, 99–108.Google Scholar
Deng, J., Ren, A.-L., Zou, J.-F. & Shao, X.-M. 2006 Three-dimensional flow around two circular cylinders in tandem arrangement. Fluid Dyn. Res. 38, 386–404.CrossRefGoogle Scholar
Griffith, M. D. & Leontini, J. S. 2017 Sharp interface immersed boundary methods and their application to vortex-induced vibration of a cylinder. J. Fluids Struct. 72, 38–58.CrossRefGoogle Scholar
Griffith, M. D., Lo Jacono, D., Sheridan, J. & Leontini, J. S. 2016 Passive heaving of elliptical cylinders with active pitching – from cylinders towards flapping foils. J. Fluids Struct. 67, 124–141.Google Scholar
Hu, J. C. & Zhou, Y. 2008 Flow structure behind two staggered circular cylinders. Part 1. Downstream evolution and classification. J. Fluid Mech. 607, 51–80.CrossRefGoogle Scholar
Huera-Huarte, F. J. & Gharib, M. 2011 Flow-induced vibrations of a side-by-side arrangement of two flexible circular cylinders. J. Fluids Struct. 27, 354–366.Google Scholar
Leontini, J. S., Thompson, M. C. & Hourigan, K. 2006 The beginning of branching behaviour of vortex-induced vibration during two-dimensional flow. J. Fluids Struct. 22, 857–864.CrossRefGoogle Scholar
Leontini, J. S., Thompson, M. C. & Hourigan, K. 2007 Three-dimensional transition in the wake of a transversely oscillating cylinder. J. Fluid Mech. 577, 79–104.CrossRefGoogle Scholar
Mittal, R., Dong, H., Bozkurttas, M., Najjar, F. M., Vargas, A. & von Loebbecke, A. 2008 A versatile sharp interface immersed boundary method for incompressible flows with complex boundaries. J. Comput. Phys. 227, 4825–4852.CrossRefGoogle ScholarPubMed
Newmark, N. M. 1959 A method of computation for structural dynamics. J. Engng Mech. 85 (3), 67–94.Google Scholar
Raghavan, K. & Bernitsas, M. M. 2011 Experimental investigation of Reynolds number effect on vortex induced vibration of rigid cylinders on elastic supports. Ocean Engng 38, 719–731.CrossRefGoogle Scholar
Singh, S. P. & Mittal, S. 2005 Vortex-induced oscillations at low Reynolds numbers: hysteresis and vortex-shedding modes. J. Fluids Struct. 20, 1085–1104.CrossRefGoogle Scholar
Sumner, D., Price, S. & Paidoussis, M. 2000 Flow-pattern identification for two staggered circular cylinders in cross-flow. J. Fluid Mech. 411, 263–303.CrossRefGoogle Scholar
Thompson, M. C., Hourigan, K. & Sheridan, J. 1996 Three-dimensional instabilities in the wake of a circular cylinder. Exp. Therm. Fluid Sci. 12, 190–196.CrossRefGoogle Scholar
Tong, F., Cheng, L. & Zhao, M. 2015 Numerical simulations of steady flow past two cylinders in staggered arrangements. J. Fluid Mech. 765, 114–149.Google Scholar
Tsui, Y. T. 1986 On wake-induced vibration of a conductor in the wake of another via a 3-D finite element method. J. Sound Vib. 107 (1), 39–58.Google Scholar
Wang, H., Yang, W., Nguyen, K. D. & Yu, G. 2014 Wake-induced vibrations of an elastically mounted cylinder located downstream of a stationary larger cylinder at low Reynolds numbers. J. Fluids Struct. 50, 479–496.Google Scholar
Williamson, C. H. K. 1988 The existence of two stages in the transition to three dimensionality of a cylinder wake. Phys. Fluids 31, 3165–3168.CrossRefGoogle Scholar
Williamson, C. H. K. & Govardhan, R. N. 2004 Vortex-induced vibrations. Annu. Rev. Fluid Mech. 36, 413–455.Google Scholar
Williamson, C. H. K. & Roshko, A. 1988 Vortex formation in the wake of an oscillating cylinder. J. Fluids Struct. 2, 355–381.Google Scholar
Yu, K. R., Étienne, S., Scolan, Y.-M., Hay, A., Fontaine, E. & Pelletier, D. 2016 Flow-induced vibrations of in-line cylinder arrangements at low Reynolds numbers. J. Fluids Struct. 60, 37–61.CrossRefGoogle Scholar
Zdravkovich, M. M. 1987 The effects of interference between circular cylinders in cross flow. J. Fluids Struct. 1 (2), 239–261.CrossRefGoogle Scholar
Zhao, M. 2013 Flow induced vibration of two rigidly coupled circular cylinders in tandem and side-by-side arrangements at a low Reynolds number of 150. Phys. Fluids 25, 123601.Google Scholar
Zhou, Y. & Alam, M. M. 2016 Wake of two interacting circular cylinders: a review. Intl J. Heat Fluid Flow 62, 510–537.Google Scholar