1 Introduction
The human heart is made of two separate volumetric pumps, the right and the left, shaded in blue and red respectively in figure 1. The former feeds the pulmonary circulation, which drives the blood flow through the lungs, and works with limited pressure differences
![]() ${\approx}2000$
Pa (15 mmHg). The left heart is, in contrast, stronger since it feeds the systemic circulation carrying oxygenated blood to the whole body (except for the lungs). The left part has, therefore, to withstand the largest pressure differences which are in the range 1.6–
${\approx}2000$
Pa (15 mmHg). The left heart is, in contrast, stronger since it feeds the systemic circulation carrying oxygenated blood to the whole body (except for the lungs). The left part has, therefore, to withstand the largest pressure differences which are in the range 1.6–
![]() $2.1\times 10^{4}$
Pa (120–160 mmHg) between atrium and ventricle in a healthy adult.
$2.1\times 10^{4}$
Pa (120–160 mmHg) between atrium and ventricle in a healthy adult.

Figure 1. Schematic description of the heart functioning. (Picture adapted from www.texasheart.org.)
The valves ensure the correct flow direction and prevent blood regurgitation. Those of the right heart are subjected to reduced fluid dynamic loads and usually are not impaired. In contrast, the aortic and mitral valves, which direct the blood from the ventricle to the aorta and from the atrium to the ventricle respectively, are subjected to the most damage.
A very simple schematic of the heart is given in figure 1; here, we limit the description to only the dynamics of the left part. During diastole, the blood from the left atrium enters the left ventricle, through the mitral valve, and recirculates in it. As systole starts, the myocardium contracts and the blood is ejected, through the aortic valve, from the left ventricle to the aorta. Although several surgical procedures are available to repair and remodel the natural valves, in some cases their replacement is unavoidable and, in those cases, choice of the optimal prosthesis is crucial. Worldwide, 280 000 valve replacements are performed each year, and this number is constantly increasing, with a projection of approximately 800 000 by 2050 due to the increasing age of the population and a growing percentage of the population accessing advanced medical care. Aortic and mitral valve replacements are almost equally distributed (Pibarot & Dumesnil Reference Pibarot and Dumesnil2009). However, while the former has already been the topic of extensive medical and scientific research, the latter has been less explored and its post-operative effects on the left ventricle dynamics still need to be analysed in detail. The main reason for this difference is that the outflow of the aortic valve goes directly into the aorta, which operates passively. In contrast, the flow produced by the mitral valve interacts directly with the left ventricle, whose dynamics is the result of the interplay between the active contraction/relaxation of the myocardium and the surface loads produced by the blood. Furthermore, the structure and the tissues composing the ventricular wall develop and change in response to the pressure and shear stresses exerted by the flow. This implies that any change in the mitral flow can lead to pathological conditions and ventricle impairment.
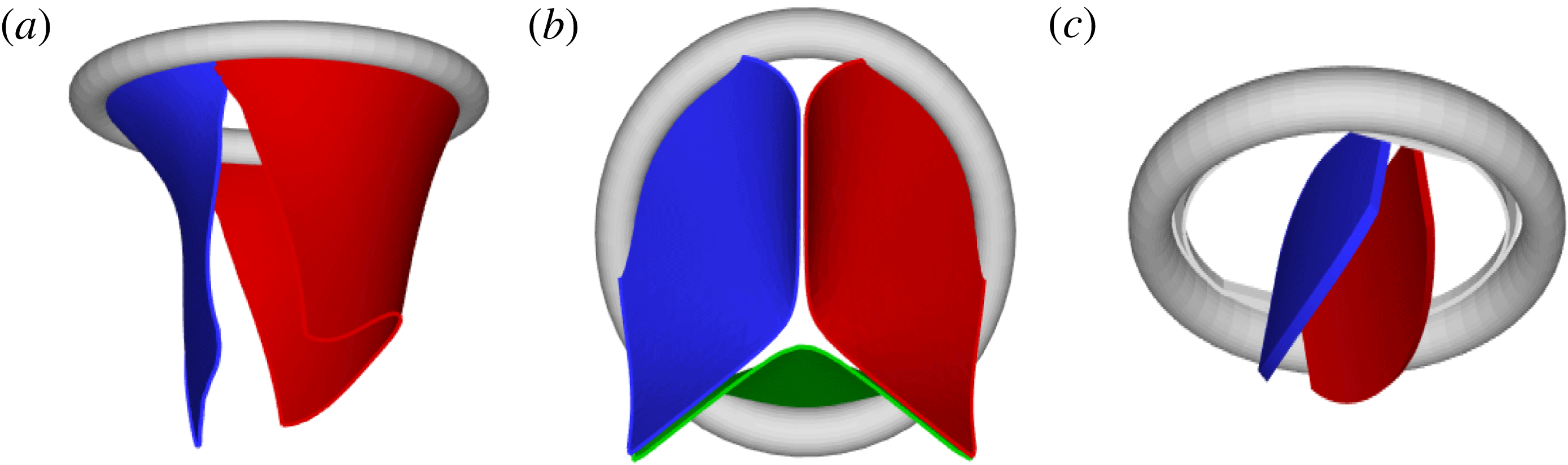
Figure 2. Different geometries of the mitral valve: (a) natural, (b) biological prosthesis, (c) mechanical prosthesis.
Accordingly, the aim of the present study is to investigate how the flow structure inside the left ventricle is altered by a mitral valve replacement for different volume fractions ejected by the left ventricle. This requires the simultaneous consideration of different prosthetic valve models (figure 2) and various levels of ventricle pumping efficiency. Concerning the first point, two alternatives are available: biological and mechanical valves. The former (figure 2 b) are prosthetic devices made of biological tissues (bovine pericardium or porcine heart valves) and have three flexible leaflets, differently from the native mitral valve which is made of two asymmetrical leaflets. These valves have good haemodynamics and reduced propensity to damage the blood cells (haemolysis) or produce clots (thrombogenesis). The drawback is, however, that their lifetime is around 15–20 years and they need to be replaced beyond this operating time. Semilunar mechanical valves (figure 2 c), instead, are made of pyrolytic carbon. They regulate the flow direction by two rigid leaflets hinged to an annular frame. The main advantage of mechanical valves is their lifelong duration. Therefore, they are indicated for patients with life expectation beyond 15 years. Their main drawback is the altered haemodynamics (de Tullio et al. Reference de Tullio, Cristallo, Balaras and Verzicco2009; Querzoli, Fortini & Cenedese Reference Querzoli, Fortini and Cenedese2010), which requires lifelong anticoagulation therapy to prevent clot formation, with its accompanying risk of bleeding and haemorrhagic events.
The pumping function of the ventricle can be quantified by its ejection fraction (
![]() $EF$
). Let
$EF$
). Let
![]() $V^{\ast }(t)$
be the volume of blood in the ventricle during the heart cycle, with a maximum
$V^{\ast }(t)$
be the volume of blood in the ventricle during the heart cycle, with a maximum
![]() $V_{M}^{\ast }$
at the end of the diastolic phase, when the myocardium is fully relaxed, and a minimum
$V_{M}^{\ast }$
at the end of the diastolic phase, when the myocardium is fully relaxed, and a minimum
![]() $V_{m}^{\ast }$
at the end of the systolic phase, when the myocardium ends its contraction. The difference
$V_{m}^{\ast }$
at the end of the systolic phase, when the myocardium ends its contraction. The difference
![]() $V_{M}^{\ast }-V_{m}^{\ast }$
is the amount of blood ejected from the ventricle during one cycle and the ratio
$V_{M}^{\ast }-V_{m}^{\ast }$
is the amount of blood ejected from the ventricle during one cycle and the ratio
![]() $(V_{M}^{\ast }-V_{m}^{\ast })/V_{M}^{\ast }=EF$
is the ejection fraction. Although this parameter has some variation among individuals, values of
$(V_{M}^{\ast }-V_{m}^{\ast })/V_{M}^{\ast }=EF$
is the ejection fraction. Although this parameter has some variation among individuals, values of
![]() $50\,\%\leqslant EF\leqslant 70\,\%$
are considered physiological,
$50\,\%\leqslant EF\leqslant 70\,\%$
are considered physiological,
![]() $40\,\%\leqslant EF\leqslant 50\,\%$
pathological and
$40\,\%\leqslant EF\leqslant 50\,\%$
pathological and
![]() $EF\leqslant 35\,\%$
life threatening.
$EF\leqslant 35\,\%$
life threatening.
Due to the synergistic interaction between the mitral flow and the ventricle dynamics, it is likely that the flow alterations induced by a prosthetic valve will have different impacts on the ventricular flow depending on its pumping efficiency. In the literature, there are a large number of studies focusing on specific aspects of the mitral flow or on the mitral valve dynamics. Among many, Faludi et al. (Reference Faludi, Szulik, D’hooge, Herijgers, Rademakers, Pedrizzetti and Voig2010), Pedrizzetti G. & Tonti (Reference Pedrizzetti G. and Tonti2010) and Querzoli et al. (Reference Querzoli, Fortini and Cenedese2010) have underlined the strong influence the mitral valve has on the diastolic flow structure, and Einstein et al. (Reference Einstein, Kunzelman, Reinhall, Nicosia and Cochran2005), Wattona et al. (Reference Wattona, Luob, Yinc, Bernaccad and Wheatleyd D.2008) and Griffith et al. (Reference Griffith, Luo, McQueen and Peskin2009) have focused on the dynamics of mitral valve leaflets. Moreover, McQueen & Peskin (Reference McQueen and Peskin2000) and Mihalef et al. (Reference Mihalef, Ionasec, Shuarma, Georgescu, Voigt, Suehling and Comanicu2011) have studied the effect of combining realistic intra-ventricular flow with a physiological mitral valve using patient-specific models without fluid–structure interaction. Vukićević et al. (Reference Vukićević, Fortini, Querzoli, Espa and Pedrizzetti2012) underlined the role of the asymmetrical structure of the native mitral valve and investigated the flow generated by a mechanical asymmetrical prosthesis. Recently, Seo et al. (Reference Seo, Vedula, Abraham, Lardo, Dawoud, Luo and Mittal2014) have analysed how the morphology and kinematics of the mitral valve can affect the left ventricular flow using a physiological mitral valve. The motion of the leaflets was, however, prescribed; thus, the synergistic interaction of the flow and the structure dynamics was imposed rather than captured by the solution.
In order to fill this gap and to simulate the complete system with the minimum number of assumptions, in this paper, a full fluid–structure interaction (FSI) model for the left ventricle and the mitral valve is used, obtaining a more realistic representation of the phenomenon. In this way, both the valve and the ventricle dynamics are determined by their interaction with the flow, which, in turn, depends on the motion of the boundaries. To limit the computational effort, we focus on two representative values of
![]() $EF$
, 60 % and 40 % respectively for healthy and pathological ventricles. Each case is simulated over several heart cycles (10 for all production runs and five for the refined cases) and the system dynamics is phase-averaged. First, the configuration with the natural mitral valve is investigated, for either healthy or impaired ventricles, and it is used as a reference case. Then, the flows with prosthetic biological and mechanical bileaflet valves are analysed and their dynamics are compared. We also assess the differences between Newtonian and non-Newtonian fluid models for the blood, and the sensitivity of the dynamics to the material properties of the valve leaflets. We believe that this study can make an important contribution to the assessment of the performance of biological and mechanical prosthetic valves for different ventricle efficiencies, this being crucial information for surgeons in the decision process of heart valve replacement.
$EF$
, 60 % and 40 % respectively for healthy and pathological ventricles. Each case is simulated over several heart cycles (10 for all production runs and five for the refined cases) and the system dynamics is phase-averaged. First, the configuration with the natural mitral valve is investigated, for either healthy or impaired ventricles, and it is used as a reference case. Then, the flows with prosthetic biological and mechanical bileaflet valves are analysed and their dynamics are compared. We also assess the differences between Newtonian and non-Newtonian fluid models for the blood, and the sensitivity of the dynamics to the material properties of the valve leaflets. We believe that this study can make an important contribution to the assessment of the performance of biological and mechanical prosthetic valves for different ventricle efficiencies, this being crucial information for surgeons in the decision process of heart valve replacement.
The structure of the paper is as follows. In the next section, the problem, the numerical model and its experimental counterpart are described. In the same section, also the flow parameters, the validation and the convergence checks are given. In § 3, the results are presented and discussed, starting from the physiological flow produced by a natural valve. This will serve as a reference case against which the flows generated by biological and mechanical valves can be evaluated. In the same section, additional simulations are presented to assess the robustness of the reference results to the specific fluid model (Newtonian versus shear-thinning non-Newtonian), to the thickness and material properties of the leaflets and to the geometrical lumen of the mitral channel. In § 4, the results are discussed in the context of the clinical literature. Closing remarks and perspectives for future studies are given in the final section.
2 The problem
2.1 Numerical and experimental set-up
The set-up of the problem is given in figure 3, showing the experimental realization and its numerical counterpart. Figure 3(b) focuses on the core of a pulse duplicator of the systemic circulation described in Meschini et al. (Reference Meschini, de Tullio, Querzoli and Verzicco2016); on an AC electrical motor, controlled by an inverter, is splined a cam which, in its rotary motion, pushes a piston driving water into a sealed Plexiglas tank with a periodic mean velocity
![]() $U^{\ast }(t)$
(figure 4
a). This flow induces a passive variation of the total volume of the system which, due to incompressibility, is copied by the ventricle (figure 4
b). The time evolution of
$U^{\ast }(t)$
(figure 4
a). This flow induces a passive variation of the total volume of the system which, due to incompressibility, is copied by the ventricle (figure 4
b). The time evolution of
![]() $U^{\ast }(t)$
in figure 4(a) is that of a pathological elderly heart in which the passive filling phase (E-wave) is much stronger than the active counterpart (A-wave) when the left atrium contracts. The cross-section of the piston and the law
$U^{\ast }(t)$
in figure 4(a) is that of a pathological elderly heart in which the passive filling phase (E-wave) is much stronger than the active counterpart (A-wave) when the left atrium contracts. The cross-section of the piston and the law
![]() $U^{\ast }(t)$
determine the stroke volume, which, in the experiments, is fixed at
$U^{\ast }(t)$
determine the stroke volume, which, in the experiments, is fixed at
![]() $V_{e}^{\ast }=90~\text{cm}^{3}$
; the minimum ventricle volume
$V_{e}^{\ast }=90~\text{cm}^{3}$
; the minimum ventricle volume
![]() $V_{m}^{\ast }$
, in contrast, can be varied continuously by adding or removing water from the sealed Plexiglas box. In this way, the ejection fraction
$V_{m}^{\ast }$
, in contrast, can be varied continuously by adding or removing water from the sealed Plexiglas box. In this way, the ejection fraction
![]() $EF=V_{e}^{\ast }/(V_{e}^{\ast }+V_{m}^{\ast })$
can be adjusted to the desired value.
$EF=V_{e}^{\ast }/(V_{e}^{\ast }+V_{m}^{\ast })$
can be adjusted to the desired value.

Figure 3. (a) Numerical set-up for the left ventricle. The bullets indicate the positions, in the symmetry
![]() $x$
–
$x$
–
![]() $z$
plane, of some relevant numerical probes. The red one is the ‘apex’ probe used to detect the apical flow stagnation. The yellow ones are used to compute the transvalvular pressure drop and the velocity in the mitral jet. The green probe is located at the ventricle centroid (
$z$
plane, of some relevant numerical probes. The red one is the ‘apex’ probe used to detect the apical flow stagnation. The yellow ones are used to compute the transvalvular pressure drop and the velocity in the mitral jet. The green probe is located at the ventricle centroid (
![]() $x=0.1$
,
$x=0.1$
,
![]() $y=0$
,
$y=0$
,
![]() $z=1.15$
) in the end-systole configuration. (b) Experimental set-up containing the left ventricle.
$z=1.15$
) in the end-systole configuration. (b) Experimental set-up containing the left ventricle.
The ventricle is a 2–3 mm thick membrane made of a transparent silicone rubber of density
![]() $\unicode[STIX]{x1D70C}_{s}^{\ast }=1040~\text{kg}~\text{m}^{-3}$
and Young modulus
$\unicode[STIX]{x1D70C}_{s}^{\ast }=1040~\text{kg}~\text{m}^{-3}$
and Young modulus
![]() $E^{\ast }=1.5~\text{MPa}$
. The density of the rubber is almost identical to that of the myocardium (
$E^{\ast }=1.5~\text{MPa}$
. The density of the rubber is almost identical to that of the myocardium (
![]() $1040~\text{kg}~\text{m}^{-3}$
versus
$1040~\text{kg}~\text{m}^{-3}$
versus
![]() $1060~\text{kg}~\text{m}^{-3}$
), while it is three times stiffer than the biological tissue (
$1060~\text{kg}~\text{m}^{-3}$
), while it is three times stiffer than the biological tissue (
![]() $E=1.5$
MPa versus max
$E=1.5$
MPa versus max
![]() $E=0.5$
MPa), and this difference was compensated by making the ventricle thickness (
$E=0.5$
MPa), and this difference was compensated by making the ventricle thickness (
![]() ${\approx}2{-}3$
mm) approximately three times smaller than that of the myocardium (
${\approx}2{-}3$
mm) approximately three times smaller than that of the myocardium (
![]() ${\leqslant}1$
cm). This is, however, still far from the real case, considering that the myocardium is anisotropic, because of the fibre orientation, and hyperelastic. In addition, during the heart cycle, the myocardium changes its stiffness from 0.02 up to 0.5 MPa and it contracts actively rather than passively, adapting to the imposed inflow as in the present study.
${\leqslant}1$
cm). This is, however, still far from the real case, considering that the myocardium is anisotropic, because of the fibre orientation, and hyperelastic. In addition, during the heart cycle, the myocardium changes its stiffness from 0.02 up to 0.5 MPa and it contracts actively rather than passively, adapting to the imposed inflow as in the present study.
The ventricle is connected to two rigid pipes of inner diameter 19 mm and 24 mm which mimic the aortic and mitral channels respectively. The distal extrema of the pipes accommodate two rigid rings (dashed line in figure 3 b) in which different valves can be fitted; any of the valves of figure 2, or a simple check valve, can be used in both positions. For the present experiments, a check valve was used in the aortic position whereas a model of the native valve, made of silicone rubber, was placed in the mitral position.
The working fluid is water, whose kinematic viscosity
![]() $\unicode[STIX]{x1D708}^{\ast }=1.2\times 10^{-6}~\text{m}^{2}~\text{s}^{-1}$
is approximately four times smaller than that of whole blood (considered as a Newtonian fluid and with a haematocrit, the volume fraction of solid cells over the total volume, of 45 %). As the Reynolds number
$\unicode[STIX]{x1D708}^{\ast }=1.2\times 10^{-6}~\text{m}^{2}~\text{s}^{-1}$
is approximately four times smaller than that of whole blood (considered as a Newtonian fluid and with a haematocrit, the volume fraction of solid cells over the total volume, of 45 %). As the Reynolds number
![]() $Re=U_{M}^{\ast }D^{\ast }/\unicode[STIX]{x1D708}^{\ast }$
and the Womersley number
$Re=U_{M}^{\ast }D^{\ast }/\unicode[STIX]{x1D708}^{\ast }$
and the Womersley number
![]() $Wo=D^{\ast }/\sqrt{T^{\ast }\unicode[STIX]{x1D708}^{\ast }}$
, with
$Wo=D^{\ast }/\sqrt{T^{\ast }\unicode[STIX]{x1D708}^{\ast }}$
, with
![]() $U_{M}^{\ast }$
the maximum of
$U_{M}^{\ast }$
the maximum of
![]() $U^{\ast }(t)$
over the diastolic phase,
$U^{\ast }(t)$
over the diastolic phase,
![]() $T^{\ast }$
the period of the cardiac cycle and
$T^{\ast }$
the period of the cardiac cycle and
![]() $D^{\ast }$
the diameter of the mitral channel, with a full-scale model (
$D^{\ast }$
the diameter of the mitral channel, with a full-scale model (
![]() $D^{\ast }=24$
mm), the velocity
$D^{\ast }=24$
mm), the velocity
![]() $U_{M}^{\ast }$
has to be four times smaller than in a real heart if we wish to operate in dynamic similarity. In our experiment, this implies that the cam frequency must be four times smaller than that of the heart in order to operate in dynamic similarity. Accordingly, the rotation rate was fixed to 15 rpm to reproduce a heart at 60 beats per minute. For an ejection fraction
$U_{M}^{\ast }$
has to be four times smaller than in a real heart if we wish to operate in dynamic similarity. In our experiment, this implies that the cam frequency must be four times smaller than that of the heart in order to operate in dynamic similarity. Accordingly, the rotation rate was fixed to 15 rpm to reproduce a heart at 60 beats per minute. For an ejection fraction
![]() $EF=60\,\%$
, we have
$EF=60\,\%$
, we have
![]() $Re=4229$
and
$Re=4229$
and
![]() $Wo=11$
, which are typical values for a physiological condition.
$Wo=11$
, which are typical values for a physiological condition.

Figure 4. (a) The time evolution of the inflow/outflow velocity,
![]() $U^{\ast }(t)$
, over a cardiac cycle. (b) The time evolution of the volume,
$U^{\ast }(t)$
, over a cardiac cycle. (b) The time evolution of the volume,
![]() $V^{\ast }(t)$
, of the left ventricle. Both plots are in dimensional units.
$V^{\ast }(t)$
, of the left ventricle. Both plots are in dimensional units.
The fluid was seeded with pine pollen particles and the system was illuminated by a laser sheet so that the flow in the vertical
![]() $x$
–
$x$
–
![]() $z$
symmetry plane could be recorded by a high-speed camera at 1000 f.p.s. An advantage of having an experiment running four times slower than the real phenomenon is the higher time resolution of the flow measurements achievable within a given frame rate of the available camera. This time stretch, however, also affects the fluid/structure interaction, which is not in dynamic similitude unless the elastic properties of the material are changed. We note, however, that in the present set-up, all of the structures are very thin and the deformable ones are relatively soft; this implies that their dynamics is dominated by the balance between external loads and added mass (see the results of § 3.3) and not by the density and stiffness of the material. Of course, the latter would change the magnitude and distribution of the structural internal stresses considerably, which, however, have not been investigated in this study.
$z$
symmetry plane could be recorded by a high-speed camera at 1000 f.p.s. An advantage of having an experiment running four times slower than the real phenomenon is the higher time resolution of the flow measurements achievable within a given frame rate of the available camera. This time stretch, however, also affects the fluid/structure interaction, which is not in dynamic similitude unless the elastic properties of the material are changed. We note, however, that in the present set-up, all of the structures are very thin and the deformable ones are relatively soft; this implies that their dynamics is dominated by the balance between external loads and added mass (see the results of § 3.3) and not by the density and stiffness of the material. Of course, the latter would change the magnitude and distribution of the structural internal stresses considerably, which, however, have not been investigated in this study.
Images (
![]() $1024\times 1280$
pixels, 0.11 mm per pixel) were processed by a variant of the classical PIV algorithm, described in detail in Falchi, Querzoli & Romano (Reference Falchi, Querzoli and Romano2006), in order to compute the two-dimensional instantaneous velocity field. The final size of the interrogation windows was
$1024\times 1280$
pixels, 0.11 mm per pixel) were processed by a variant of the classical PIV algorithm, described in detail in Falchi, Querzoli & Romano (Reference Falchi, Querzoli and Romano2006), in order to compute the two-dimensional instantaneous velocity field. The final size of the interrogation windows was
![]() $31\times 31$
pixels, with a 50 % overlap. The uncertainty in the particle displacement measurement was approximately 0.1 pixel.
$31\times 31$
pixels, with a 50 % overlap. The uncertainty in the particle displacement measurement was approximately 0.1 pixel.
The computational model was aimed at reproducing as closely as possible the above described experiment. Figure 3(a) shows the computational domain, which is periodic in the two horizontal directions and allows for inflow/outflow in the vertical direction. Over the upper surface, an inflow is imposed through the mitral channel when
![]() $U(t)$
is positive and an outflow through the aortic channel when
$U(t)$
is positive and an outflow through the aortic channel when
![]() $U(t)$
is negative. The flow rate through the bottom wall is adjusted at each time step so to ensure incompressibility and to preserve the total fluid volume. In the numerical model, all of the variables are presented in non-dimensional form, with the velocities scaled by
$U(t)$
is negative. The flow rate through the bottom wall is adjusted at each time step so to ensure incompressibility and to preserve the total fluid volume. In the numerical model, all of the variables are presented in non-dimensional form, with the velocities scaled by
![]() $U_{M}^{\ast }$
, the lengths by
$U_{M}^{\ast }$
, the lengths by
![]() $D^{\ast }$
and the times by the cycle period
$D^{\ast }$
and the times by the cycle period
![]() $T^{\ast }$
; non-dimensional variables are indicated without superscript
$T^{\ast }$
; non-dimensional variables are indicated without superscript
![]() $\ast$
.
$\ast$
.
The mitral and aortic channels together with the valve planes (in red in figure 3 a) are modelled as a rigid structure which is used as a frame to anchor the deformable ventricle and the valve leaflets, respectively in grey, green and blue in figure 3(a).
In the experimental set-up, a simple check valve was placed in the aortic position. In order to replicate this simple behaviour, we used a porous medium in the aortic channel with a time-dependent porosity (de Tullio, Pedrizzetti & Verzicco Reference de Tullio, Pedrizzetti and Verzicco2011). During diastole, the medium porosity goes to zero, thus obstructing the duct and preventing fluid from entering the aortic channel. During systole, the porosity tends to infinity and fluid can leave the ventricle to enter the aorta.
The reference frame is as shown in figure 3(a), with the positive
![]() $z$
pointing vertically downward and the origin
$z$
pointing vertically downward and the origin
![]() $z=0$
at the mitral annulus. The
$z=0$
at the mitral annulus. The
![]() $x$
–
$x$
–
![]() $z$
plane at
$z$
plane at
![]() $y=0$
is a symmetry plane for the system.
$y=0$
is a symmetry plane for the system.
The flow volume is disseminated with 36 numerical probes which provide a continuous pointwise sampling of all velocity and vorticity components and the pressure. The most relevant are the ‘apex’ probe (the red bullet in figure 3
a at
![]() $z=2.5$
), the ‘centroid’ probe (the green bullet in figure 3
a at
$z=2.5$
), the ‘centroid’ probe (the green bullet in figure 3
a at
![]() $x=0.1$
,
$x=0.1$
,
![]() $y=0$
,
$y=0$
,
![]() $z=1.15$
) and the three ‘mitral’ probes (the yellow bullets at
$z=1.15$
) and the three ‘mitral’ probes (the yellow bullets at
![]() $z=0$
, 0.75 and 1.5) which are used to analyse the time evolution of velocity and pressure.
$z=0$
, 0.75 and 1.5) which are used to analyse the time evolution of velocity and pressure.
2.2 The numerical method
The computational model is basically that described by de Tullio & Pascazio (Reference de Tullio and Pascazio2016) and Spandan et al. (Reference Spandan, Meschini, de Tullio, Querzoli, Lohse and Verzicco2017), which consists of a flow solver two-way coupled with a structure solver. The resulting assembly is computationally efficient and flexible enough to allow for the solution of a wide range of problems ranging from multiphase flows to turbulence in complex geometries. All of the details of the algorithms, the validations and the convergence checks can be found in the above references; only the main features are summarized here.
The flow is incompressible and viscous; thus, its motion is described by the Navier–Stokes equations, which in non-dimensional form read
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \frac{\unicode[STIX]{x2202}\boldsymbol{u}}{\unicode[STIX]{x2202}t}+\boldsymbol{u}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}=-\unicode[STIX]{x1D735}p+\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D749}+\boldsymbol{f},\\ \displaystyle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{ u}=0.\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \frac{\unicode[STIX]{x2202}\boldsymbol{u}}{\unicode[STIX]{x2202}t}+\boldsymbol{u}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}=-\unicode[STIX]{x1D735}p+\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D749}+\boldsymbol{f},\\ \displaystyle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{ u}=0.\end{array}\right\}\end{eqnarray}$$
Here,
![]() $\boldsymbol{u}$
is the velocity,
$\boldsymbol{u}$
is the velocity,
![]() $p$
is the pressure and
$p$
is the pressure and
![]() $\boldsymbol{f}$
is a specific body force term which is used to enforce the boundary condition at the various fluid/structure interfaces. For all but one case, the blood has been considered as a Newtonian fluid since it is known that its non-Newtonian features become relevant only in vessels of diameter smaller than 15–20 red blood cell diameters (
$\boldsymbol{f}$
is a specific body force term which is used to enforce the boundary condition at the various fluid/structure interfaces. For all but one case, the blood has been considered as a Newtonian fluid since it is known that its non-Newtonian features become relevant only in vessels of diameter smaller than 15–20 red blood cell diameters (
![]() ${\sim}80$
–
${\sim}80$
–
![]() $100~\unicode[STIX]{x03BC}\text{m}$
) (Siginer, De Kee & Chhabra Reference Siginer, De Kee and Chhabra1999). The viscous term of (2.1) then reads
$100~\unicode[STIX]{x03BC}\text{m}$
) (Siginer, De Kee & Chhabra Reference Siginer, De Kee and Chhabra1999). The viscous term of (2.1) then reads
![]() $\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D749}=\unicode[STIX]{x1D6FB}^{2}\boldsymbol{u}/Re$
. The flow solver, however, can also simulate more complex constitutive relations (De Vita, de Tullio & Verzicco Reference De Vita, de Tullio and Verzicco2016). In one case (§ 3.2), in order to show the effect of a non-Newtonian fluid, the Carreau–Yasuda shear-thinning model has been used. In this fluid, the kinematic viscosity
$\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D749}=\unicode[STIX]{x1D6FB}^{2}\boldsymbol{u}/Re$
. The flow solver, however, can also simulate more complex constitutive relations (De Vita, de Tullio & Verzicco Reference De Vita, de Tullio and Verzicco2016). In one case (§ 3.2), in order to show the effect of a non-Newtonian fluid, the Carreau–Yasuda shear-thinning model has been used. In this fluid, the kinematic viscosity
![]() $\unicode[STIX]{x1D708}$
depends on the magnitude of the rate-of-strain tensor
$\unicode[STIX]{x1D708}$
depends on the magnitude of the rate-of-strain tensor
![]() $S=|\unicode[STIX]{x1D64E}|=|\unicode[STIX]{x1D735}\boldsymbol{u}+\unicode[STIX]{x1D735}\boldsymbol{u}^{\text{T}}|/2$
according to
$S=|\unicode[STIX]{x1D64E}|=|\unicode[STIX]{x1D735}\boldsymbol{u}+\unicode[STIX]{x1D735}\boldsymbol{u}^{\text{T}}|/2$
according to
![]() $\unicode[STIX]{x1D708}(S)=\unicode[STIX]{x1D708}_{\infty }+(\unicode[STIX]{x1D708}_{0}-\unicode[STIX]{x1D708}_{\infty })[1+(\unicode[STIX]{x1D706}S)^{2}]^{b}$
. With this fluid model, the viscous term of (2.1) becomes
$\unicode[STIX]{x1D708}(S)=\unicode[STIX]{x1D708}_{\infty }+(\unicode[STIX]{x1D708}_{0}-\unicode[STIX]{x1D708}_{\infty })[1+(\unicode[STIX]{x1D706}S)^{2}]^{b}$
. With this fluid model, the viscous term of (2.1) becomes
![]() $\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D749}=\unicode[STIX]{x1D735}\boldsymbol{\cdot }[2\unicode[STIX]{x1D708}(S)\unicode[STIX]{x1D64E}]/(\unicode[STIX]{x1D708}_{\infty }Re)$
, the Reynolds number being computed using the
$\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D749}=\unicode[STIX]{x1D735}\boldsymbol{\cdot }[2\unicode[STIX]{x1D708}(S)\unicode[STIX]{x1D64E}]/(\unicode[STIX]{x1D708}_{\infty }Re)$
, the Reynolds number being computed using the
![]() $\unicode[STIX]{x1D708}_{\infty }$
viscosity. As already done in De Vita et al. (Reference De Vita, de Tullio and Verzicco2016), in the present study we have also selected the parameters of the fluid model to mimic a healthy adult male with a haematocrit (ratio of the cell volume to the whole blood volume) of 40 %, which yields
$\unicode[STIX]{x1D708}_{\infty }$
viscosity. As already done in De Vita et al. (Reference De Vita, de Tullio and Verzicco2016), in the present study we have also selected the parameters of the fluid model to mimic a healthy adult male with a haematocrit (ratio of the cell volume to the whole blood volume) of 40 %, which yields
![]() $\unicode[STIX]{x1D706}=3.313$
s,
$\unicode[STIX]{x1D706}=3.313$
s,
![]() $b=-0.3216$
,
$b=-0.3216$
,
![]() $\unicode[STIX]{x1D708}_{\infty }=3.7\times 10^{-6}~\text{m}^{2}~\text{s}^{-1}$
and
$\unicode[STIX]{x1D708}_{\infty }=3.7\times 10^{-6}~\text{m}^{2}~\text{s}^{-1}$
and
![]() $\unicode[STIX]{x1D708}_{0}=4.3\unicode[STIX]{x1D708}_{\infty }$
.
$\unicode[STIX]{x1D708}_{0}=4.3\unicode[STIX]{x1D708}_{\infty }$
.
The structure deformation is solved using a spring–mass method which is based on an interaction potential approach (Tanaka, Wado & Nakamura Reference Tanaka, Wado and Nakamura2012) and applied to different problems by de Tullio & Pascazio (Reference de Tullio and Pascazio2016) and Spandan et al. (Reference Spandan, Meschini, de Tullio, Querzoli, Lohse and Verzicco2017). Here, the wet surfaces of the ventricle and mitral valve are discretized using triangular elements with a uniform distribution of the body mass on their vertices. The nodes are connected by springs of elastic constant
![]() $k_{e}$
, and two triangles sharing an edge have a bending stiffness
$k_{e}$
, and two triangles sharing an edge have a bending stiffness
![]() $k_{b}$
. When the resulting network deforms due to external forces, internal potential energy is stored in the system according to
$k_{b}$
. When the resulting network deforms due to external forces, internal potential energy is stored in the system according to
![]() $W=k_{e}(\ell -\ell _{0})^{2}/2+k_{b}(1-\cos (\unicode[STIX]{x1D703}-\unicode[STIX]{x1D703}_{0}))$
, where
$W=k_{e}(\ell -\ell _{0})^{2}/2+k_{b}(1-\cos (\unicode[STIX]{x1D703}-\unicode[STIX]{x1D703}_{0}))$
, where
![]() $\ell$
and
$\ell$
and
![]() $\unicode[STIX]{x1D703}$
are respectively the vector connecting two vertices of an edge and the angle between the normals of two triangles sharing that edge;
$\unicode[STIX]{x1D703}$
are respectively the vector connecting two vertices of an edge and the angle between the normals of two triangles sharing that edge;
![]() $\ell _{0}$
and
$\ell _{0}$
and
![]() $\unicode[STIX]{x1D703}_{0}$
are the same quantities in the reference stress-free configuration (figure 5). The internal forces in the structure can be computed through
$\unicode[STIX]{x1D703}_{0}$
are the same quantities in the reference stress-free configuration (figure 5). The internal forces in the structure can be computed through
![]() $\boldsymbol{F}_{int}=-\unicode[STIX]{x1D735}W$
, which, together with the external forces
$\boldsymbol{F}_{int}=-\unicode[STIX]{x1D735}W$
, which, together with the external forces
![]() $\boldsymbol{F}_{ext}$
, allows for the solution of Newton’s second law for each node
$\boldsymbol{F}_{ext}$
, allows for the solution of Newton’s second law for each node
![]() $m_{n}\ddot{\boldsymbol{x}}=\boldsymbol{F}_{int}+\boldsymbol{F}_{ext}$
, with
$m_{n}\ddot{\boldsymbol{x}}=\boldsymbol{F}_{int}+\boldsymbol{F}_{ext}$
, with
![]() $m_{n}$
the mass associated with the node. From the acceleration, by successive integrations, the velocity
$m_{n}$
the mass associated with the node. From the acceleration, by successive integrations, the velocity
![]() $\dot{\boldsymbol{x}}$
and the position
$\dot{\boldsymbol{x}}$
and the position
![]() $\boldsymbol{x}$
of the nodes are computed, thus yielding the updated configuration of the structure.
$\boldsymbol{x}$
of the nodes are computed, thus yielding the updated configuration of the structure.
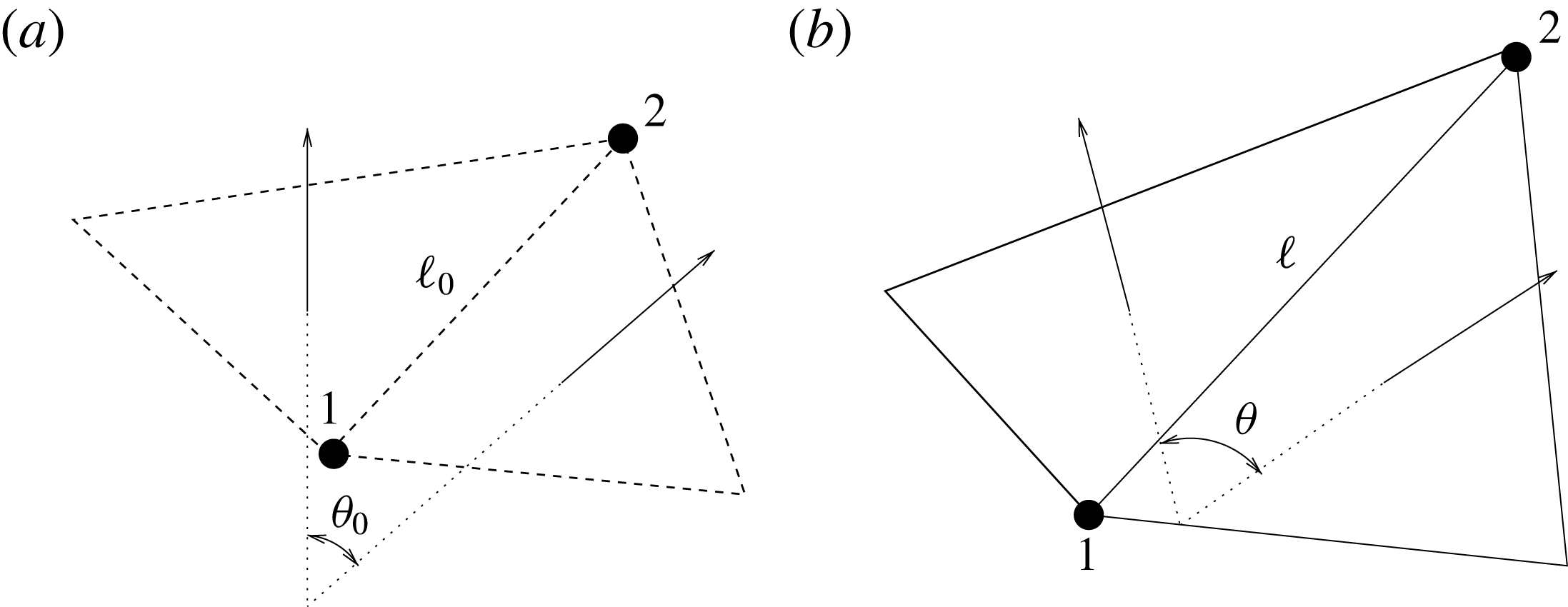
Figure 5. (a) Undeformed configuration of the structure. (b) Deformed structure configuration.
In the present study, in which the structures are essentially isotropic membranes, the elastic constants
![]() $k_{e}$
and
$k_{e}$
and
![]() $k_{b}$
are computed using the Van Gelder model (Reference Van Gelder1998) via
$k_{b}$
are computed using the Van Gelder model (Reference Van Gelder1998) via
![]() $k_{e}=Eh(A_{1}+A_{2})/\ell _{0}^{2}$
and
$k_{e}=Eh(A_{1}+A_{2})/\ell _{0}^{2}$
and
![]() $k_{b}=B2/\sqrt{3}$
, where
$k_{b}=B2/\sqrt{3}$
, where
![]() $E$
and
$E$
and
![]() $B$
are respectively the Young modulus of the material and the bending stiffness of the structure,
$B$
are respectively the Young modulus of the material and the bending stiffness of the structure,
![]() $h$
is the local membrane thickness, and
$h$
is the local membrane thickness, and
![]() $A_{1}$
and
$A_{1}$
and
![]() $A_{2}$
are the areas of the two triangles sharing the edge
$A_{2}$
are the areas of the two triangles sharing the edge
![]() $\ell _{0}$
. As shown in de Tullio & Pascazio (Reference de Tullio and Pascazio2016), the method can be extended to nonlinear as well as anisotropic materials. This is certainly the case for biological tissues, which are hyperelastic and orthotropic. In this investigation, however, with reference experiments performed with silicone rubber as membrane material, this additional feature was not necessary and it has not been activated in our simulations.
$\ell _{0}$
. As shown in de Tullio & Pascazio (Reference de Tullio and Pascazio2016), the method can be extended to nonlinear as well as anisotropic materials. This is certainly the case for biological tissues, which are hyperelastic and orthotropic. In this investigation, however, with reference experiments performed with silicone rubber as membrane material, this additional feature was not necessary and it has not been activated in our simulations.
The presence of the structure on the fluid, and vice versa, is enforced through immersed boundary (IB) methods. Two IB techniques are implemented in the code: the direct forcing of Fadlun et al. (Reference Fadlun, Verzicco, Orlandi and Mohd-Yosuf2000) is used for the rigid still parts, while for the moving and deformable surfaces, the moving-least-squares approach of Vannella & Balaras (Reference Vannella and Balaras2009) is used because, even if computationally more expensive, it yields smooth hydrodynamic loads which result in a more accurate description of the structure dynamics.
All of the above modules are controlled by an FSI algorithm which is implemented in either the ‘strong’ or the ‘loose’ coupling mode. After an extensive series of preliminary simulations, convergence checks and validations, it was determined that the most effective strategy is a loose coupling approach combined with a time substepping for the structure dynamics. Briefly, from the flow and structure at the time
![]() $t^{n}$
, the flow at the new time (
$t^{n}$
, the flow at the new time (
![]() $t^{n+1}=t^{n}+\unicode[STIX]{x0394}t$
) is computed; the hydrodynamic loads at the old and new times are then used to advance the structure with a time substep
$t^{n+1}=t^{n}+\unicode[STIX]{x0394}t$
) is computed; the hydrodynamic loads at the old and new times are then used to advance the structure with a time substep
![]() $\unicode[STIX]{x0394}t_{s}=\unicode[STIX]{x0394}t/S$
,
$\unicode[STIX]{x0394}t_{s}=\unicode[STIX]{x0394}t/S$
,
![]() $S$
being the number of substeps, until the time
$S$
being the number of substeps, until the time
![]() $t^{n+1}$
is reached. This procedure needs the flow solution and the IB procedure only once per time step and requires multiple solutions only of the structure part, which, being much faster than the rest, does not penalize the overall performance.
$t^{n+1}$
is reached. This procedure needs the flow solution and the IB procedure only once per time step and requires multiple solutions only of the structure part, which, being much faster than the rest, does not penalize the overall performance.
Since the present problem involves the dynamics of membranes in a fluid, an important component of the simulation is the model of their contact. A common practice is to introduce a repulsive force that increases as the distance between two bodies decreases (Tanaka et al. Reference Tanaka, Wado and Nakamura2012) to induce a ‘rebound’ when they get close enough. However, when a heart valve closes, the leaflets must stay in contact in order to prevent regurgitation, and an approach based on the repulsive force generates instabilities and stiffens the numerical problem. As an alternative, we have defined, over the computational mesh, an array that is null in the fluid phase and assumes a specific (integer) value in the cells occupied by each body. Its values are updated every time step, and when, during the integration, a triangle ends up in a non-null cell, it means that the position is already occupied by another triangle. In this case, the velocities of both surface elements are set to their average, so that they can still freely move together in space but cannot compenetrate. On the other hand, when the system dynamics brings two contacting triangles far apart, they can evolve according to the computed trajectory. We will see in the following that this approach allows the valve to close without prescribing a contact surface, but, at the same time, it prevents compenetration between the leaflets and between the leaflets and the ventricle.
Before concluding this section, we wish to mention that at the initial stage of this study, in order to save computational time, we have tried to prescribe the motion of the valve leaflets and to limit the fluid/structure interaction only to the ventricle dynamics. This approach resulted in considerable computational savings (more than 60 %–70 %), but it yielded results that were strongly dependent on the plausibility of the assigned (guessed) leaflet motion. Any mismatch between the real and the assigned leaflet position resulted in the generation of vortex structures that were shed from the valve and propagated into the flow. In addition, we will see that there is a substantial cycle-to-cycle variation in the flow. Therefore, even if the valve dynamics is properly guessed in a cycle, it might be not in another cycle, thus spoiling the overall quality of the solution.
2.3 Simulation parameters, grid convergence and experimental validation
All of the numerical simulations have been run for a set-up as in figure 3(a) on a mesh of
![]() $129^{3}$
nodes evenly distributed in all three directions. The ventricle has been discretized by
$129^{3}$
nodes evenly distributed in all three directions. The ventricle has been discretized by
![]() $3\times 10^{4}$
triangles while the two leaflets of the natural mitral valve (figure 3
a) have a total of
$3\times 10^{4}$
triangles while the two leaflets of the natural mitral valve (figure 3
a) have a total of
![]() $8\times 10^{3}$
triangles. The Lagrangian (triangle) resolution is approximately 70 % of the local Eulerian grid spacing, in order to correctly impose the boundary conditions on the bodies. The time integration has been performed at constant Courant number
$8\times 10^{3}$
triangles. The Lagrangian (triangle) resolution is approximately 70 % of the local Eulerian grid spacing, in order to correctly impose the boundary conditions on the bodies. The time integration has been performed at constant Courant number
![]() $CFL=0.2$
with a dynamic time step that adjusts during the integration so to maintain the CFL constant. The substepping for the integration of the structure is fixed at
$CFL=0.2$
with a dynamic time step that adjusts during the integration so to maintain the CFL constant. The substepping for the integration of the structure is fixed at
![]() $S=50$
. The specific values of the time-step size depend on the ejection fraction of the ventricle; typical figures for
$S=50$
. The specific values of the time-step size depend on the ejection fraction of the ventricle; typical figures for
![]() $EF=40\,\%$
(
$EF=40\,\%$
(
![]() $EF=60\,\%$
) are
$EF=60\,\%$
) are
![]() $1.5\times 10^{4}$
(
$1.5\times 10^{4}$
(
![]() $3\times 10^{4}$
) time steps per cycle with a single-processor equivalent CPU time of
$3\times 10^{4}$
) time steps per cycle with a single-processor equivalent CPU time of
![]() ${\approx}20$
h (
${\approx}20$
h (
![]() ${\approx}40$
h). The computational load increases steeply as the simulation is refined. For a run at
${\approx}40$
h). The computational load increases steeply as the simulation is refined. For a run at
![]() $EF=60\,\%$
on a mesh of
$EF=60\,\%$
on a mesh of
![]() $193^{3}$
nodes with
$193^{3}$
nodes with
![]() $4.2\times 10^{4}$
triangles for the ventricle and
$4.2\times 10^{4}$
triangles for the ventricle and
![]() $1.2\times 10^{4}$
for both leaflets, the number of time steps per cycle ramps up to
$1.2\times 10^{4}$
for both leaflets, the number of time steps per cycle ramps up to
![]() $5\times 10^{4}$
, with the single-processor equivalent CPU time
$5\times 10^{4}$
, with the single-processor equivalent CPU time
![]() ${\approx}170$
h. For the same physical case, in a further refined simulation, the number of computational nodes has been increased to
${\approx}170$
h. For the same physical case, in a further refined simulation, the number of computational nodes has been increased to
![]() $257^{3}$
, the triangular elements for all of the structures to
$257^{3}$
, the triangular elements for all of the structures to
![]() $6.8\times 10^{4}$
and the required number of time steps per cycle to
$6.8\times 10^{4}$
and the required number of time steps per cycle to
![]() ${\approx}9.2\times 10^{4}$
, and the single-processor equivalent CPU time is slightly smaller than 2000 h. Due to the large computational cost of the refined cases, the simulations on the
${\approx}9.2\times 10^{4}$
, and the single-processor equivalent CPU time is slightly smaller than 2000 h. Due to the large computational cost of the refined cases, the simulations on the
![]() $193^{3}$
and
$193^{3}$
and
![]() $257^{3}$
grids were run ‘only’ for five heart cycles, while all of the other production cases were run for 10 heart cycles.
$257^{3}$
grids were run ‘only’ for five heart cycles, while all of the other production cases were run for 10 heart cycles.
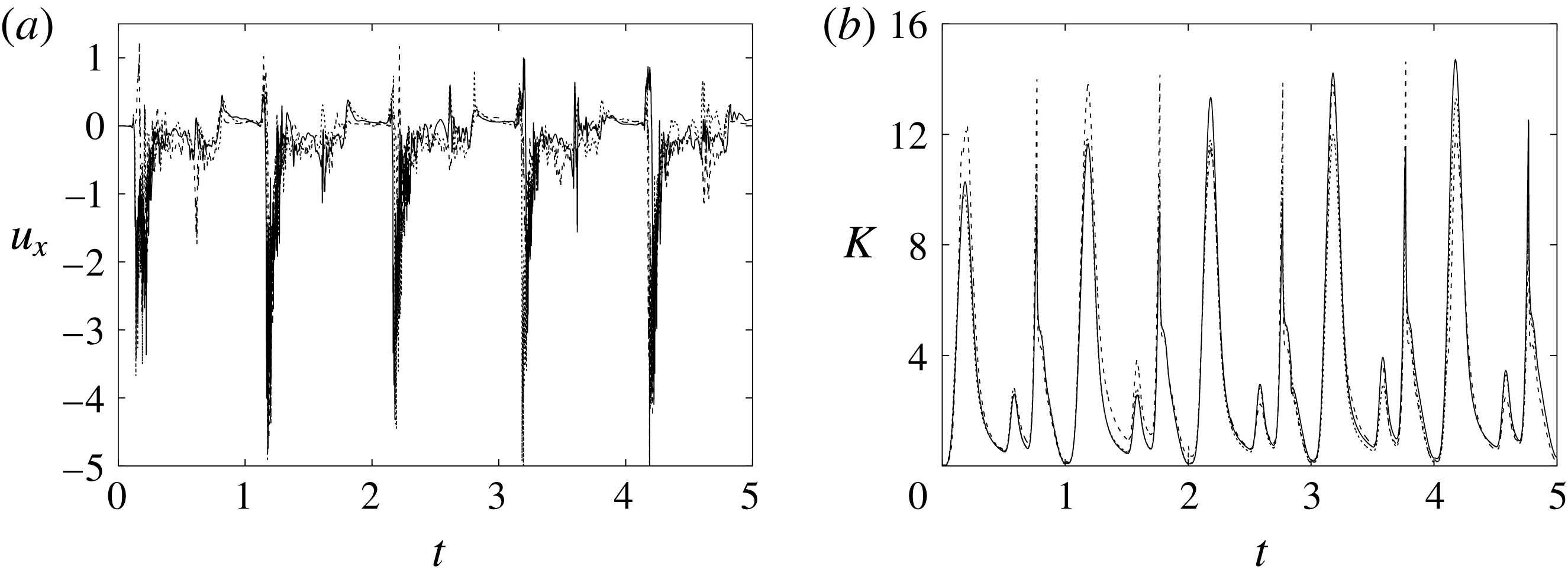
Figure 6. (a) Plot of the instantaneous values of the
![]() $x$
-velocity component at the probe placed at the apex of the left ventricle. (b) Kinetic energy of the flow inside the left ventricle. Curves:
$x$
-velocity component at the probe placed at the apex of the left ventricle. (b) Kinetic energy of the flow inside the left ventricle. Curves:
![]() $\cdots \cdots$
, grid with
$\cdots \cdots$
, grid with
![]() $257^{3}$
nodes; – – – –, grid with
$257^{3}$
nodes; – – – –, grid with
![]() $193^{3}$
nodes; ——, grid with
$193^{3}$
nodes; ——, grid with
![]() $129^{3}$
nodes. The inflow/outflow curve is as in figure 4(a).
$129^{3}$
nodes. The inflow/outflow curve is as in figure 4(a).
Figure 6 shows the time series for the
![]() $x$
component of the velocity sampled at the ventricle apex probe (see figure 3
a) and for the kinetic energy of the flow inside the ventricle: the results are shown for the very fine (
$x$
component of the velocity sampled at the ventricle apex probe (see figure 3
a) and for the kinetic energy of the flow inside the ventricle: the results are shown for the very fine (
![]() $257^{3}$
), refined (
$257^{3}$
), refined (
![]() $193^{3}$
) and basic (
$193^{3}$
) and basic (
![]() $129^{3}$
) meshes. There is substantial agreement among the results, although a considerable cycle-to-cycle variation can be noted, which makes instantaneous comparison of the various quantities difficult. This is due to the dynamics of the small scales that are produced by the turbulent cascade transferring energy from the largest flow scales up to the smallest dissipative structures. The small flow scales tend to have chaotic dynamics and can only be described statistically. In the present case, in order to filter out these turbulent fluctuations, the data have been phase-averaged over 10 cycles (five for the finer grids) and the results are reported in figure 7(a,b), evidencing an improvement of the agreement, which, however, still shows non-negligible differences. For this reason, in figure 7(a), in addition to the phase-averaged data, three instantaneous profiles from each case are reported in the background. It can be noted that the amplitude of the instantaneous fluctuations can be up to five times larger than the differences between the phase-averaged profiles, thus suggesting that it is the insufficient statistical convergence rather than the inadequate spatial resolution that produces the discrepancies. As a confirmation of this conjecture, we note that the largest deviations occur in those parts of the cycle where the fluctuations are the largest. Additional evidence of the resolution quality comes from the instantaneous flow snapshots and the spatial profiles (shown later in this paper), which do not evidence the
$129^{3}$
) meshes. There is substantial agreement among the results, although a considerable cycle-to-cycle variation can be noted, which makes instantaneous comparison of the various quantities difficult. This is due to the dynamics of the small scales that are produced by the turbulent cascade transferring energy from the largest flow scales up to the smallest dissipative structures. The small flow scales tend to have chaotic dynamics and can only be described statistically. In the present case, in order to filter out these turbulent fluctuations, the data have been phase-averaged over 10 cycles (five for the finer grids) and the results are reported in figure 7(a,b), evidencing an improvement of the agreement, which, however, still shows non-negligible differences. For this reason, in figure 7(a), in addition to the phase-averaged data, three instantaneous profiles from each case are reported in the background. It can be noted that the amplitude of the instantaneous fluctuations can be up to five times larger than the differences between the phase-averaged profiles, thus suggesting that it is the insufficient statistical convergence rather than the inadequate spatial resolution that produces the discrepancies. As a confirmation of this conjecture, we note that the largest deviations occur in those parts of the cycle where the fluctuations are the largest. Additional evidence of the resolution quality comes from the instantaneous flow snapshots and the spatial profiles (shown later in this paper), which do not evidence the
![]() $\unicode[STIX]{x1D6FF}$
-waves (or wiggles) that typically appear when an energy-conserving integration scheme is employed with coarse spatial resolution.
$\unicode[STIX]{x1D6FF}$
-waves (or wiggles) that typically appear when an energy-conserving integration scheme is employed with coarse spatial resolution.
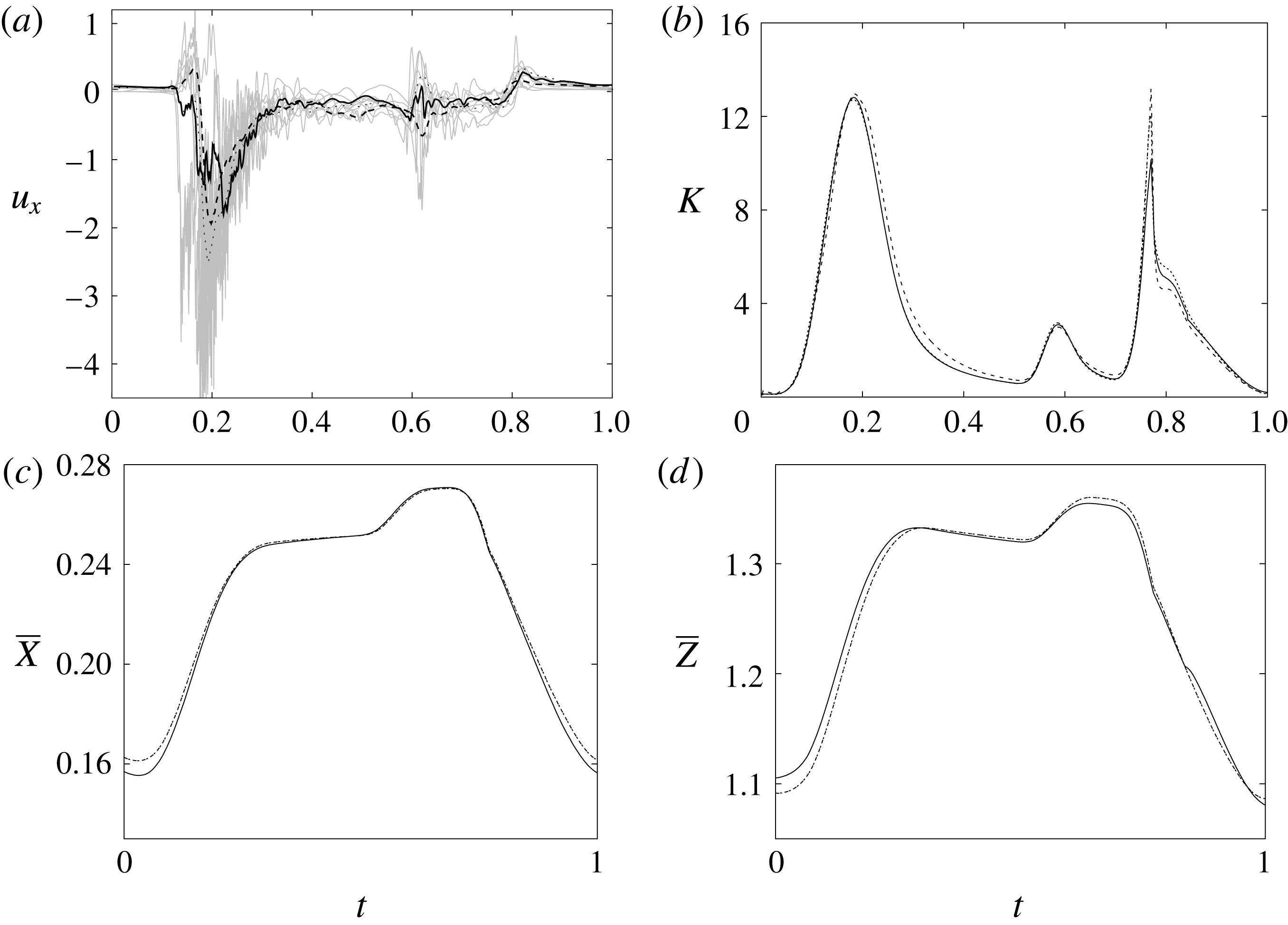
Figure 7. (a) Phase-averaged values of the
![]() $x$
-velocity at the apex probe. The grey profiles in the background are instantaneous values (three for each case) reported to evidence the amplitude of the fluctuations. (b) Phase-averaged kinetic energy of the flow inside the ventricle. (c) Phase-averaged
$x$
-velocity at the apex probe. The grey profiles in the background are instantaneous values (three for each case) reported to evidence the amplitude of the fluctuations. (b) Phase-averaged kinetic energy of the flow inside the ventricle. (c) Phase-averaged
![]() $X$
-centroid of the ventricle contour. (d) Phase-averaged
$X$
-centroid of the ventricle contour. (d) Phase-averaged
![]() $Z$
-centroid of the ventricle contour. Curves:
$Z$
-centroid of the ventricle contour. Curves:
![]() $\cdots \cdots$
, grid with
$\cdots \cdots$
, grid with
![]() $257^{3}$
nodes; – – – –, grid with
$257^{3}$
nodes; – – – –, grid with
![]() $193^{3}$
nodes; ——, grid with
$193^{3}$
nodes; ——, grid with
![]() $129^{3}$
nodes. The inflow/outflow curve is as in figure 4(a).
$129^{3}$
nodes. The inflow/outflow curve is as in figure 4(a).
Since in these simulations not only the flow but also the structure dynamics is part of the solution, in figure 7(c,d), we report the time evolution of the
![]() $\overline{X}$
- and
$\overline{X}$
- and
![]() $\overline{Z}$
-centroids of the ventricle. An additional quantity that has been monitored in this grid refinement check is the evolution of the velocity magnitude at the probe located at the centroid of the ventricle, and the instantaneous as well as the phase-averaged values are reported in figure 8, again showing satisfactory agreement. The agreement of the profiles in figure 8(b) looks better than that in figure 7(a), and, as explained above, this is due to the smaller fluctuations (compare figures 8
a and 6
a), which ease the convergence of the phase-averaged quantities.
$\overline{Z}$
-centroids of the ventricle. An additional quantity that has been monitored in this grid refinement check is the evolution of the velocity magnitude at the probe located at the centroid of the ventricle, and the instantaneous as well as the phase-averaged values are reported in figure 8, again showing satisfactory agreement. The agreement of the profiles in figure 8(b) looks better than that in figure 7(a), and, as explained above, this is due to the smaller fluctuations (compare figures 8
a and 6
a), which ease the convergence of the phase-averaged quantities.
The motion of the valve leaflet results properly captured by the combination of Eulerian/Lagrangian meshes of this study is also shown in figure 8(c) for the posterior mitral leaflet.
Before concluding this discussion on the grid refinement check, it is worthwhile to mention that the Reynolds number
![]() $Re=4229$
of the flow is computed using the peak velocity of the E-wave (figure 4
a), which lasts only for a small fraction of the cycle. In this problem, the cycle-averaged velocity is zero and its root mean square (r.m.s.) is only
$Re=4229$
of the flow is computed using the peak velocity of the E-wave (figure 4
a), which lasts only for a small fraction of the cycle. In this problem, the cycle-averaged velocity is zero and its root mean square (r.m.s.) is only
![]() $0.158~V_{peak}$
, with the Reynolds number reduced proportionally. In addition, the flow is pulsatile and the time window during which the Reynolds number remains large is too short to allow the flow to transition to fully developed turbulence (in which the energy cascades down up to the Kolmogorov scale). This implies that the usual order of magnitude estimates used for homogeneous isotropic turbulence of statistically steady flows do not apply directly here and the only reliable check is a grid refinement, as described above.
$0.158~V_{peak}$
, with the Reynolds number reduced proportionally. In addition, the flow is pulsatile and the time window during which the Reynolds number remains large is too short to allow the flow to transition to fully developed turbulence (in which the energy cascades down up to the Kolmogorov scale). This implies that the usual order of magnitude estimates used for homogeneous isotropic turbulence of statistically steady flows do not apply directly here and the only reliable check is a grid refinement, as described above.
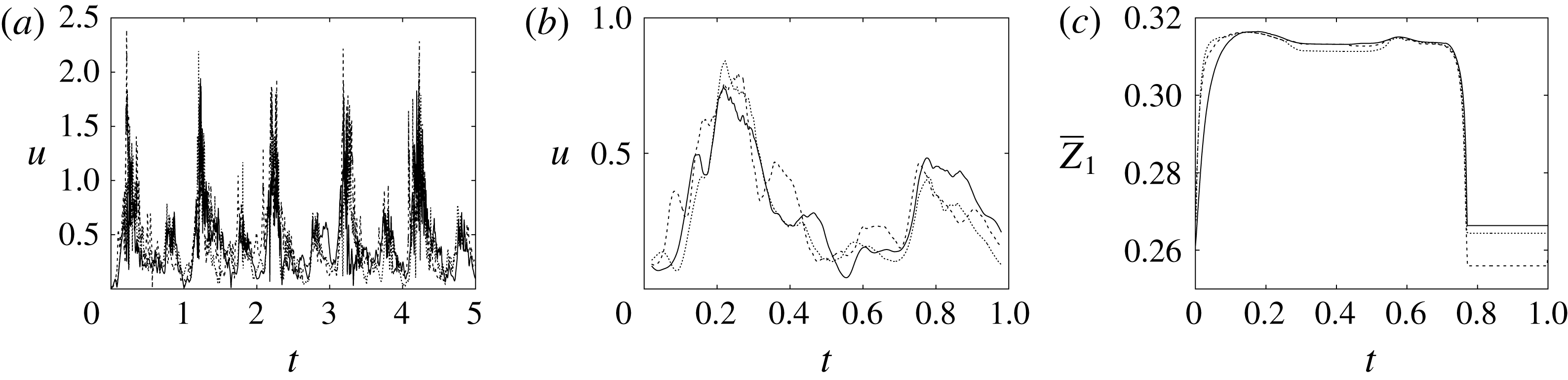
Figure 8. (a) Plot of the instantaneous values of the velocity magnitude at the probe placed at the ventricle centroid (green probe of figure 3
a). (b) The same as (a) but for the phase-averaged velocity. (c) The phase-averaged
![]() $Z$
-centroid of the posterior leaflet of the mitral valve. Curves:
$Z$
-centroid of the posterior leaflet of the mitral valve. Curves:
![]() $\cdots \cdots$
, grid with
$\cdots \cdots$
, grid with
![]() $257^{3}$
nodes; – – – –, grid with
$257^{3}$
nodes; – – – –, grid with
![]() $193^{3}$
nodes; ——, grid with
$193^{3}$
nodes; ——, grid with
![]() $129^{3}$
nodes. The inflow/outflow curve is as in figure 4(a).
$129^{3}$
nodes. The inflow/outflow curve is as in figure 4(a).
Of course, even if the output of the numerical code is grid-independent, this does not imply that the results are physically reliable and that they reproduce the intended problem correctly. For this reason, we have also compared the numerical data with an ad hoc laboratory experiment run for identical dynamical conditions. We measured the instantaneous two-dimensional velocity field in the
![]() $x$
–
$x$
–
![]() $z$
symmetry plane and the shape of the ventricle, which are shown for representative phases of the cycle in figures 9–11. It can be observed that the dynamics of the main jet and the main recirculations are satisfactorily matched and also the motion of the ventricle compares well. Also satisfactory can be considered the comparison of the horizontal profiles of the vertical velocity and the vertical profiles of the horizontal velocity extracted at the symmetry plane
$z$
symmetry plane and the shape of the ventricle, which are shown for representative phases of the cycle in figures 9–11. It can be observed that the dynamics of the main jet and the main recirculations are satisfactorily matched and also the motion of the ventricle compares well. Also satisfactory can be considered the comparison of the horizontal profiles of the vertical velocity and the vertical profiles of the horizontal velocity extracted at the symmetry plane
![]() $y=0$
during diastole and systole (figure 10). When evaluating the quality of the agreement, it should be considered that, while the numerical data are phase-averaged over 10 cycles, the experimental points are instantaneous since quantitative acquisitions were run only for one cycle.
$y=0$
during diastole and systole (figure 10). When evaluating the quality of the agreement, it should be considered that, while the numerical data are phase-averaged over 10 cycles, the experimental points are instantaneous since quantitative acquisitions were run only for one cycle.

Figure 9. Comparison between experimental measurements (a,c) and numerical results (b,d) of the flow inside the left ventricle, respectively at the peak of the E-wave
![]() $t=0.2$
and at late systole
$t=0.2$
and at late systole
![]() $t=0.9$
. The inflow/outflow curve is as in figure 4(a).
$t=0.9$
. The inflow/outflow curve is as in figure 4(a).
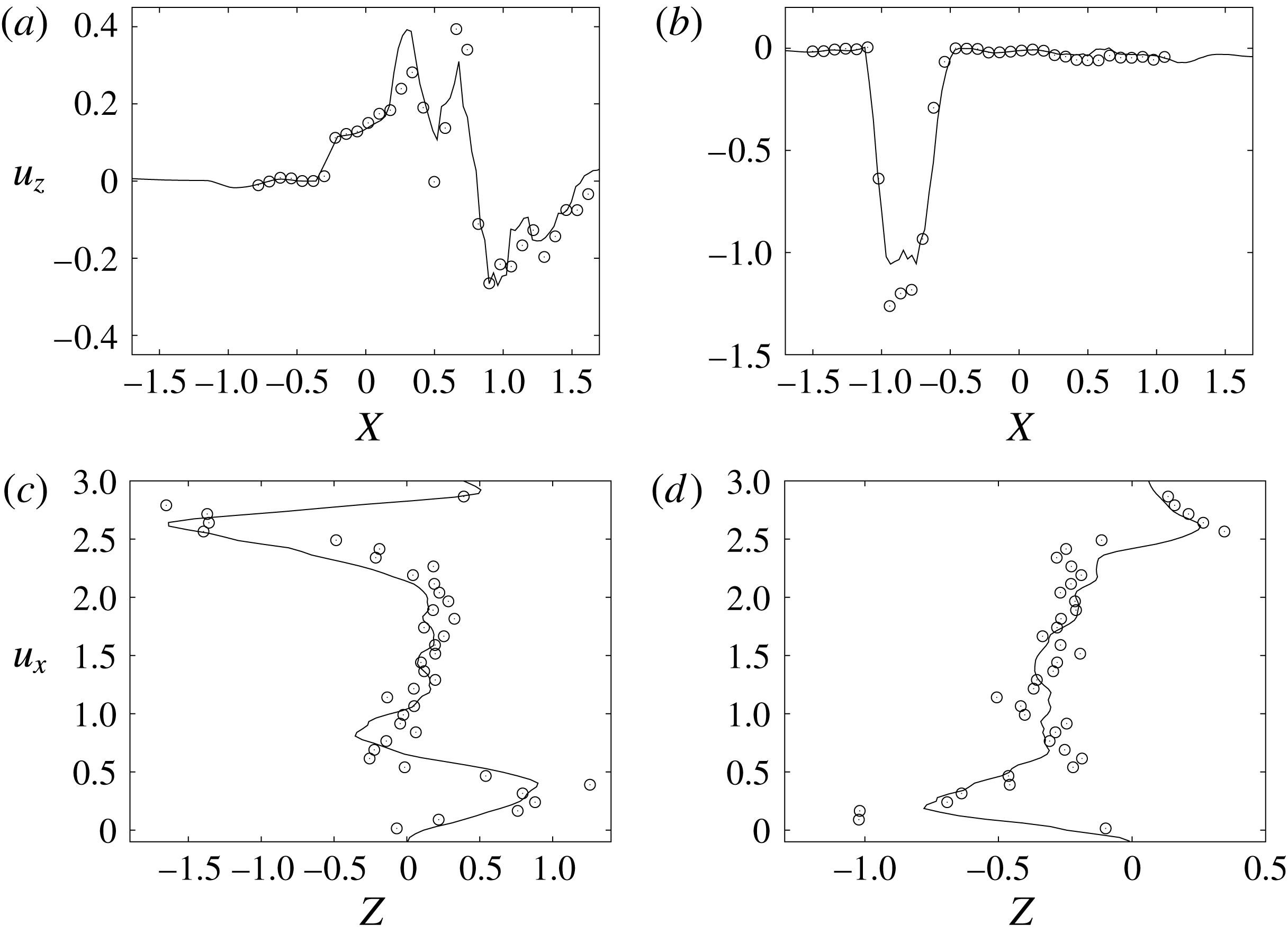
Figure 10. Comparison between experimental measurements (○) and numerical results (——) for velocity profiles in the symmetry plane (
![]() $y=0$
). (a,b) Horizontal section at
$y=0$
). (a,b) Horizontal section at
![]() $z=1$
: (a) E-wave
$z=1$
: (a) E-wave
![]() $t=0.25$
, (b) peak systole at
$t=0.25$
, (b) peak systole at
![]() $t=0.8$
. (c,d) Vertical section at
$t=0.8$
. (c,d) Vertical section at
![]() $x=0$
: (c) E-wave
$x=0$
: (c) E-wave
![]() $t=0.25$
, (d) peak systole at
$t=0.25$
, (d) peak systole at
![]() $t=0.8$
. The velocities
$t=0.8$
. The velocities
![]() $u_{x}$
and
$u_{x}$
and
![]() $u_{z}$
are normalized with the peak value of the E-wave.
$u_{z}$
are normalized with the peak value of the E-wave.
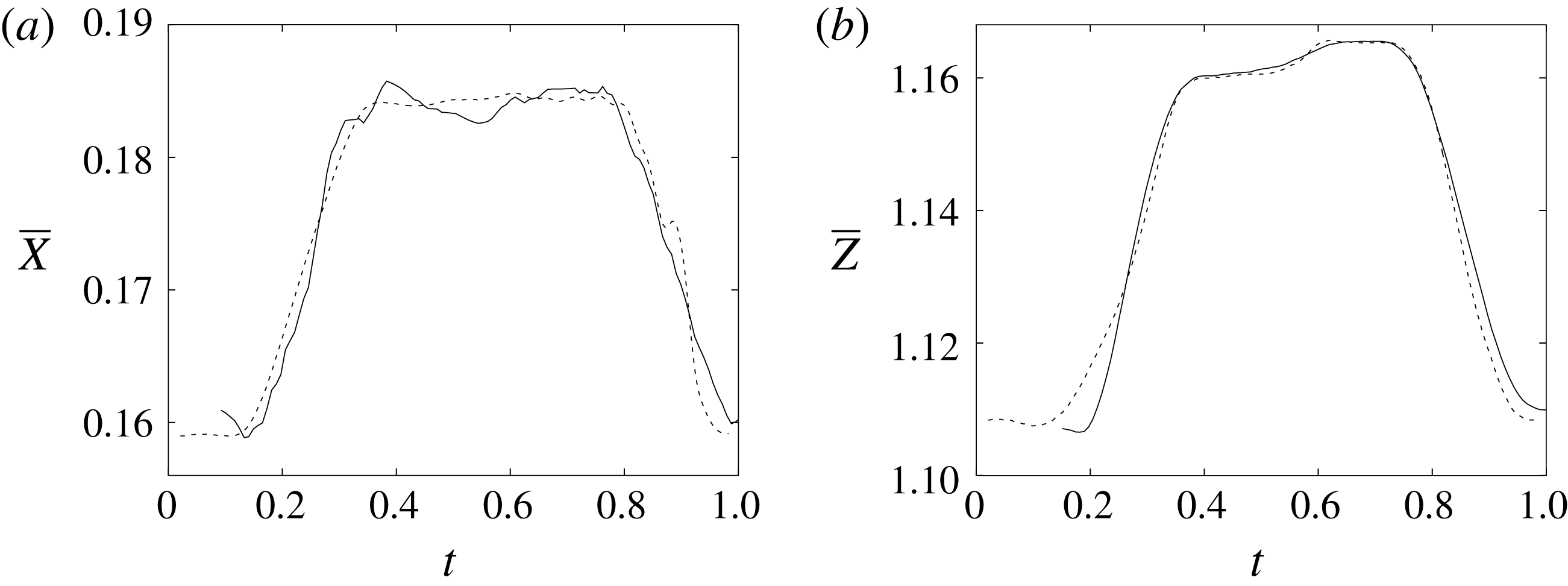
Figure 11. (a) Phase-averaged
![]() $X$
-centroid of the evolution in time of the ventricle contour. (b) Phase-averaged
$X$
-centroid of the evolution in time of the ventricle contour. (b) Phase-averaged
![]() $Z$
-centroid of the evolution in time of the ventricle contour. Curves: ——, numerical; – – – –, experimental results. The inflow/outflow curve is as in figure 4(a).
$Z$
-centroid of the evolution in time of the ventricle contour. Curves: ——, numerical; – – – –, experimental results. The inflow/outflow curve is as in figure 4(a).
3 Results
In this section, the results obtained for two different ejection fractions and three types of mitral valve are discussed and compared. The first reference case, which will be used as a guideline to distinguish between physiological and pathological behaviours, is that of an efficient ventricle (
![]() $EF=60\,\%$
) with a natural mitral valve (figure 2
a). In this case, the flow rate during the cycle is that shown in figure 12, with a ratio of the inflow peaks at the E- and A-waves of
$EF=60\,\%$
) with a natural mitral valve (figure 2
a). In this case, the flow rate during the cycle is that shown in figure 12, with a ratio of the inflow peaks at the E- and A-waves of
![]() ${\approx}0.5$
.
${\approx}0.5$
.
In a successive section, the same healthy ventricle configuration will be simulated with a non-Newtonian shear-thinning (Carreau–Yasuda) fluid model in order to validate the Newtonian fluid assumption used for the rest of the paper.
Section 3.3 is devoted to assessment of the sensitivity of the solution to the material properties and membrane thicknesses used to model the leaflets of natural and biological prosthetic valves. This analysis has been performed since there is a great deal of variability among individuals of the biological tissue properties and, if the solution were too sensitive to a specific set of values, any conclusion should be limited only to the specific case and would not be general. In the same section, also the effects of a reduced section available to the flow (stenotic valve) are briefly described to further stress the importance of comparing different valve models within the same mitral orifice area.
The flow in a ventricle with low pumping efficiency (figure 12, dashed line) will then be considered in order to assess the effect of a deteriorated ejection fraction, characterizing an unhealthy ventricle, on the system dynamics. As already mentioned, the Reynolds number for
![]() $EF=60\,\%$
is
$EF=60\,\%$
is
![]() $Re=4229$
, and it is based on the dimensional peak velocity at the E-wave. If the same velocity were used to compute the Reynolds number at
$Re=4229$
, and it is based on the dimensional peak velocity at the E-wave. If the same velocity were used to compute the Reynolds number at
![]() $EF=40\,\%$
, a smaller value would be obtained (
$EF=40\,\%$
, a smaller value would be obtained (
![]() ${\approx}2000$
). However, in order to have a more immediate comparison between the two cases, we have decided to leave the Reynolds number fixed at
${\approx}2000$
). However, in order to have a more immediate comparison between the two cases, we have decided to leave the Reynolds number fixed at
![]() $Re=4229$
and to rescale the inflow/outflow velocity profile as in the dashed line of figure 12.
$Re=4229$
and to rescale the inflow/outflow velocity profile as in the dashed line of figure 12.
Both ventricle conditions have then been evaluated either with a trileaflet biological or with a bileaflet mechanical mitral valve to analyse the effects of a prosthetic valve on the ventricle and flow dynamics.
It is worth mentioning that all of the valves (figure 2
a–c) are such as to fit into a mitral orifice of
![]() $D^{\ast }=24$
mm, and their geometries have been obtained by drawings and anatomical sketches. In reality, depending on the specific valve model (stented or stentless, curved or straight leaflets, etc.) and on the surgical implantation technique (balloon-expandable transcatheter or open heart), different valve sizes can be positioned within a given
$D^{\ast }=24$
mm, and their geometries have been obtained by drawings and anatomical sketches. In reality, depending on the specific valve model (stented or stentless, curved or straight leaflets, etc.) and on the surgical implantation technique (balloon-expandable transcatheter or open heart), different valve sizes can be positioned within a given
![]() $D^{\ast }$
. Moreover, it is possible to implant different valve sizes in the same patient by resorting to the ‘oversizing’ practice (Blanke et al.
Reference Blanke, Willson, Webb, Achenbach, Piazza, Min, Pache and Leipsic2014) or by positioning the valve in the ‘supra-annular’ position (Sung et al.
Reference Sung, Chang, Lee and Woo2008). This implies that the present results should be interpreted as a general trend of the system rather then as a performance assessment of a specific device.
$D^{\ast }$
. Moreover, it is possible to implant different valve sizes in the same patient by resorting to the ‘oversizing’ practice (Blanke et al.
Reference Blanke, Willson, Webb, Achenbach, Piazza, Min, Pache and Leipsic2014) or by positioning the valve in the ‘supra-annular’ position (Sung et al.
Reference Sung, Chang, Lee and Woo2008). This implies that the present results should be interpreted as a general trend of the system rather then as a performance assessment of a specific device.
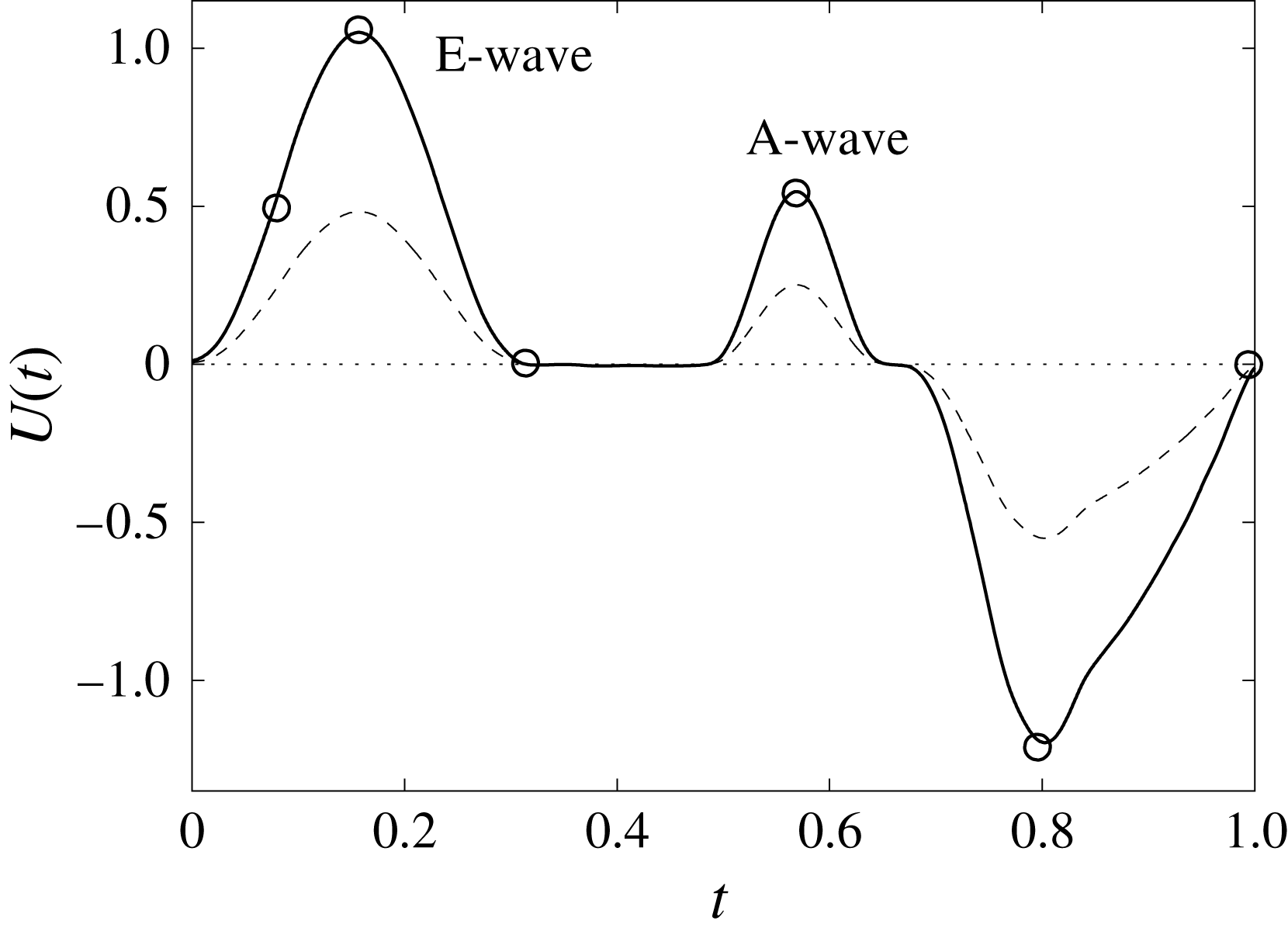
Figure 12. The flow rate in the ventricle
![]() $U(t)$
during the cycle: ——,
$U(t)$
during the cycle: ——,
![]() $EF=60\,\%$
; – – – –,
$EF=60\,\%$
; – – – –,
![]() $EF=40\,\%$
. The circles on the
$EF=40\,\%$
. The circles on the
![]() $EF=60\,\%$
line indicate the representative times of the cycle in which the solution is shown later.
$EF=60\,\%$
line indicate the representative times of the cycle in which the solution is shown later.
3.1 The reference case: healthy ventricle and natural valve
The reference case consists of a left ventricle with an ejection fraction of 60 % and a natural mitral valve with the anterior leaflet, the one closer to the aortic channel, slightly longer than the posterior one (figure 2 a).

Figure 13. Snapshots of the velocity vector in the
![]() $x$
–
$x$
–
![]() $z$
symmetry plane and contours of the vertical velocity (the range is
$z$
symmetry plane and contours of the vertical velocity (the range is
![]() $-2\leqslant v_{z}\leqslant 2$
from blue to red) at
$-2\leqslant v_{z}\leqslant 2$
from blue to red) at
![]() $EF=60\,\%$
with a natural mitral valve. The different instants of the cardiac cycle are indicated in figure 12 by the symbol ○. (a) Early E-wave, (b) peak of the E-wave, (c) during diastasis, (d) peak of the A-wave, (e) peak systole and (e) end of systole. The dashed lines of (b) and (d) evidence the sections at
$EF=60\,\%$
with a natural mitral valve. The different instants of the cardiac cycle are indicated in figure 12 by the symbol ○. (a) Early E-wave, (b) peak of the E-wave, (c) during diastasis, (d) peak of the A-wave, (e) peak systole and (e) end of systole. The dashed lines of (b) and (d) evidence the sections at
![]() $z=1$
and
$z=1$
and
![]() $z=2$
over which the velocity profiles in figures 14 and 15 are reported.
$z=2$
over which the velocity profiles in figures 14 and 15 are reported.
Following the curve of figure 12, we see that at the beginning of the diastole, the E-wave strengthens, the flow rate through the mitral orifice increases and the valve opens, thus producing an intense jet. Due to the asymmetry of the leaflets, the jet is initially directed towards the ventricle wall, where it starts to sweep the endocardium (figure 13 a). Once the peak of the flow rate is reached, the valve leaflets open wider and the jet points vertically downward, reaching the ventricle apex (figure 13 b) and generating a strong recirculation. (figure 13 c). The process repeats during the A-wave, with a new injection of momentum that further strengthens the large-scale vortex. This recirculation lasts for a large fraction of the cycle (approximately 50 %), and it is very beneficial for the haemodynamics since it constantly sweeps the endocardium and prevents the formation of stagnant flow regions (Fortini et al. Reference Fortini, Querzoli, Espa and Cenedese2013). When the systole starts, the flow leaves the ventricle from both the aortic and the mitral channel. The orientation of the mitral leaflets, however, is such as to prevent a continuous regurgitation, and the low pressure, induced by the incipient back flow accelerating between the leaflets, seals them (figure 13 e). Beyond this point, the flow can leave the ventricle only through the aortic channel, the ventricle shrinks and the outflow decreases until the initial volume is recovered and the ventricle is ready for a new cardiac cycle.
Similar features, in a somehow more quantitative way, can be deduced from figures 14 and 15, showing phase-averaged mean and r.m.s. vertical velocity profiles along the horizontal sections
![]() $z=1$
and
$z=1$
and
![]() $z=2$
in the symmetry plane
$z=2$
in the symmetry plane
![]() $y=0$
. For the sake of conciseness, the profiles are shown only for the peaks of the E- and A-waves when the strongest mitral jets are produced. At these instants of the cycle, the positions of the sections are evidenced by dashed lines in figure 13(b,d). Figures 14–15 show the same quantities also for a biological trileaflet and a mechanical bileaflet prosthetic valve in order to compare the different flow behaviours; each case will be discussed in a dedicated section.
$y=0$
. For the sake of conciseness, the profiles are shown only for the peaks of the E- and A-waves when the strongest mitral jets are produced. At these instants of the cycle, the positions of the sections are evidenced by dashed lines in figure 13(b,d). Figures 14–15 show the same quantities also for a biological trileaflet and a mechanical bileaflet prosthetic valve in order to compare the different flow behaviours; each case will be discussed in a dedicated section.
The natural valve, at the peak of the E-wave (figures 14 a and 15 a), produces a smooth and regular jet that induces a ventricle flow recirculation, evidenced by the negative velocity region to the left of the jet. Despite the relatively large excursions of the valve leaflets, the mitral jet remains compact in space, thus providing, within a fixed momentum (in turn depending on the ejection fraction), the highest penetration capability and the smallest pressure losses among all the valves (see also the discussion in § 4). Both features are beneficial to prevent flow stagnation inside the ventricle.
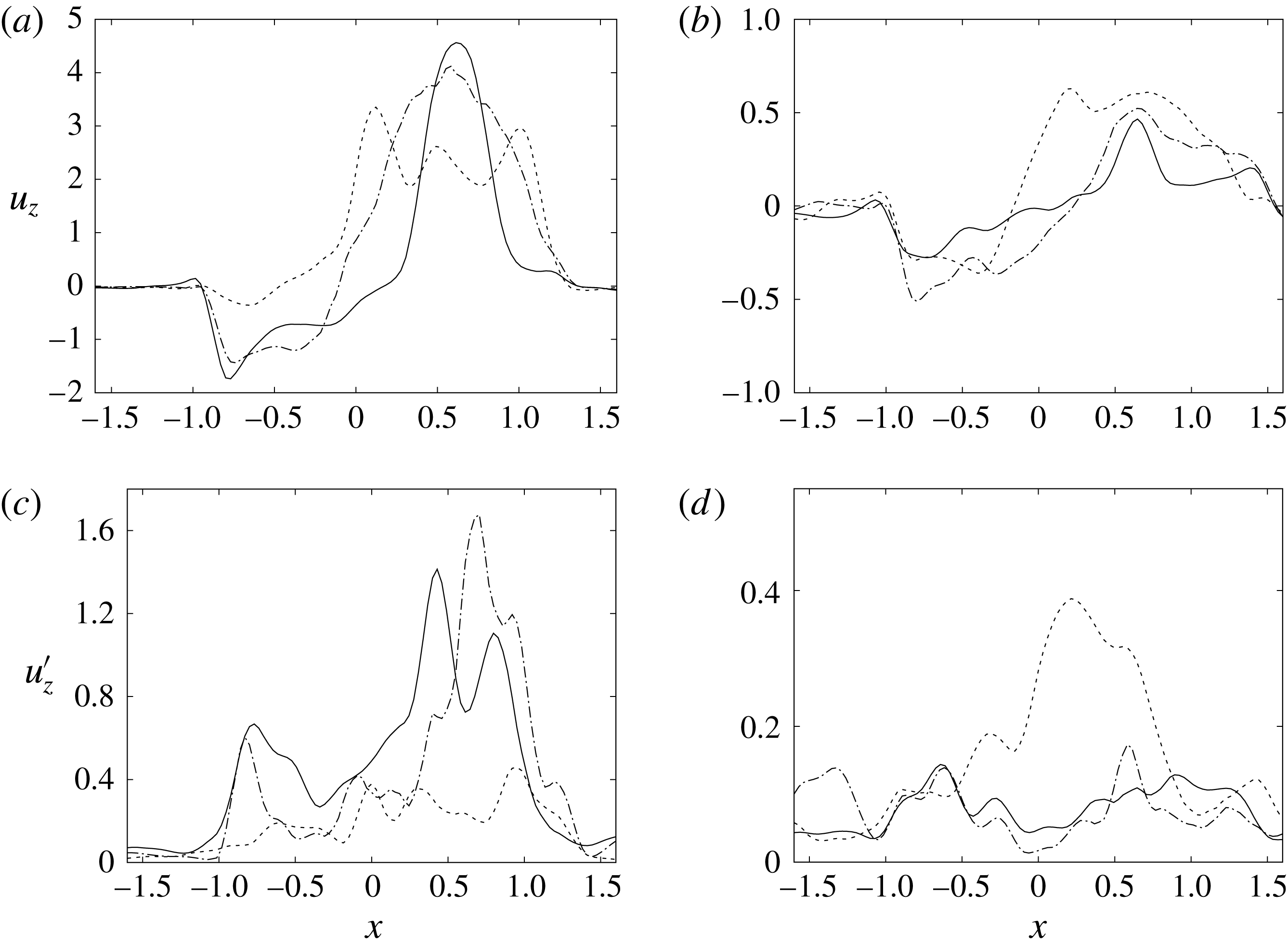
Figure 14. Phase-averaged vertical (
![]() $z$
) velocity profiles at the section
$z$
) velocity profiles at the section
![]() $z=1$
; (a,b) for mean velocity, (c,d) for r.m.s. fluctuations. (a,c) Peak of E-wave, (b,d) peak of A-wave. Curves: ——, natural valve; – – – –, mechanical prosthesis; — ⋅ —, biological prosthesis.
$z=1$
; (a,b) for mean velocity, (c,d) for r.m.s. fluctuations. (a,c) Peak of E-wave, (b,d) peak of A-wave. Curves: ——, natural valve; – – – –, mechanical prosthesis; — ⋅ —, biological prosthesis.
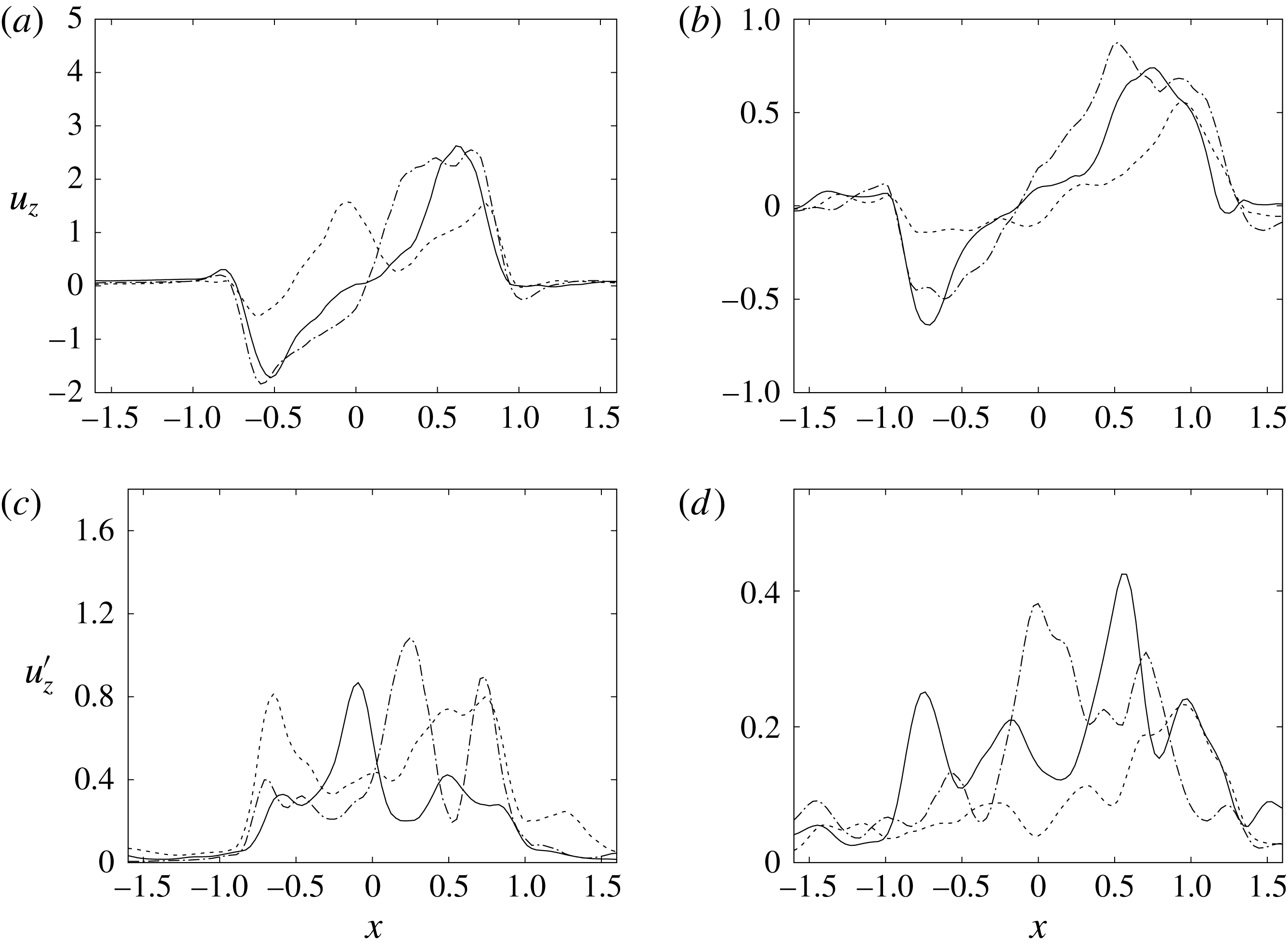
Figure 15. The same as figure 14 but for the section
![]() $z=2$
.
$z=2$
.
This strong jet assures the presence of a persistent vortex during most of the heart cycle which constantly sweeps the ventricle surface and avoids the formation of regions of stagnant fluid, a phenomenon referred to as blood stasis, a particularly undesired condition (Cordero et al. Reference Cordero, Rossini, Martinez-Lagazpi, Del Villar, Benito, Barrio, Fernandez-Aviles, Yotti, del Alamo and Bermejo2015).
In order to monitor the motion of the fluid during the cycle, we report in figure 16(a) the time evolution of the velocity magnitude sampled at the apex probe shown in figure 3(a). One can note the peak of the velocity at
![]() $t=0.2$
, caused by the maximum of the E-wave (
$t=0.2$
, caused by the maximum of the E-wave (
![]() $t\approx 0.16$
), followed by the velocity decay during the diastasis (
$t\approx 0.16$
), followed by the velocity decay during the diastasis (
![]() $0.3\leqslant t\leqslant 0.5$
). Even at the end of the diastasis, however, the fluid is not at rest and the occurrence of the A-wave (
$0.3\leqslant t\leqslant 0.5$
). Even at the end of the diastasis, however, the fluid is not at rest and the occurrence of the A-wave (
![]() $t\approx 0.56$
) produces a new velocity peak although with reduced magnitude. Similar information is obtained from the kinetic energy of the fluid within the ventricle shown in figure 16(b). Here, we note also that during the systole (
$t\approx 0.56$
) produces a new velocity peak although with reduced magnitude. Similar information is obtained from the kinetic energy of the fluid within the ventricle shown in figure 16(b). Here, we note also that during the systole (
![]() $0.65\leqslant t\leqslant 1$
), the energy of the fluid increases again due to the intense velocities in the region around the aortic channel. The sudden energy drop at
$0.65\leqslant t\leqslant 1$
), the energy of the fluid increases again due to the intense velocities in the region around the aortic channel. The sudden energy drop at
![]() $t\approx 0.78$
indicates fast closure of the mitral valve, which prevents blood regurgitation towards the left atrium and allows flow only through the aorta.
$t\approx 0.78$
indicates fast closure of the mitral valve, which prevents blood regurgitation towards the left atrium and allows flow only through the aorta.
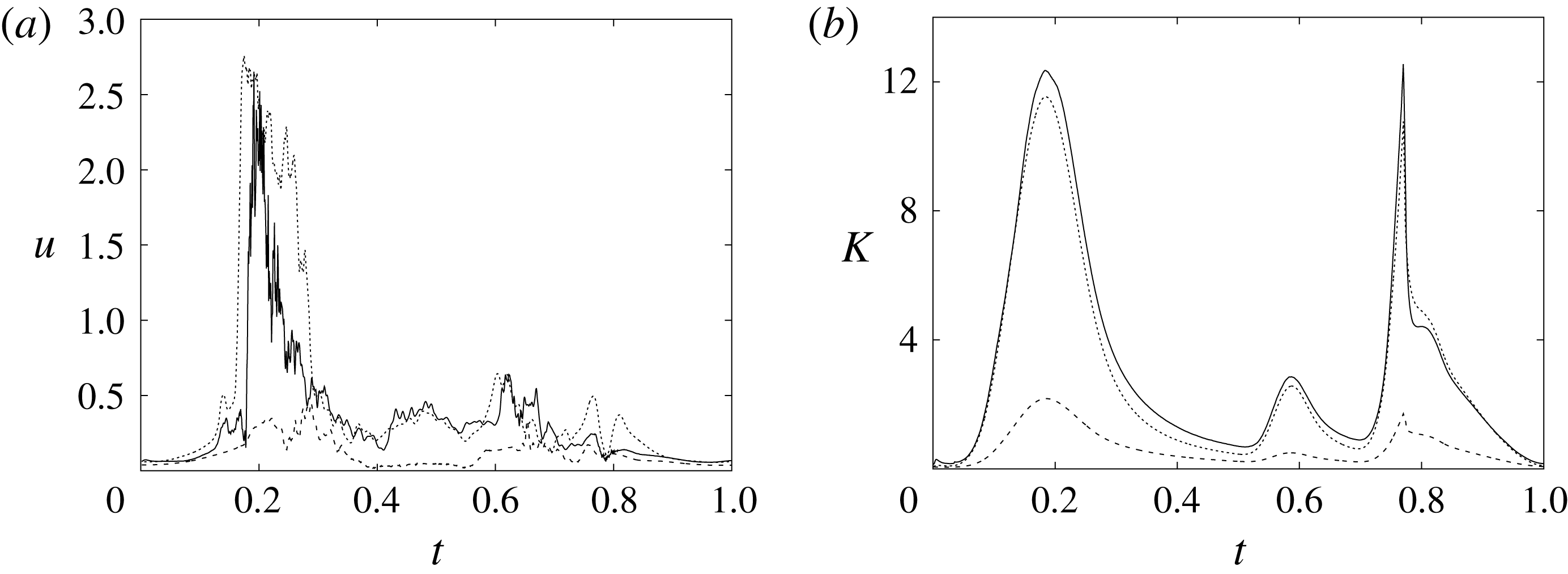
Figure 16. (a) Phase-averaged evolution of the velocity magnitude,
![]() $u$
, at the apex probe with the natural mitral valve. (b) Kinetic energy of the flow inside the ventricle. Curves: ——,
$u$
, at the apex probe with the natural mitral valve. (b) Kinetic energy of the flow inside the ventricle. Curves: ——,
![]() $EF=60\,\%$
; – – – –,
$EF=60\,\%$
; – – – –,
![]() $EF=40\,\%$
;
$EF=40\,\%$
;
![]() $\cdots \cdots$
,
$\cdots \cdots$
,
![]() $EF=60\,\%$
with non-Newtonian fluid model.
$EF=60\,\%$
with non-Newtonian fluid model.
The plot of figure 17 confirms the above argument by showing the strong leaflet retraction during the closing phase, which occurs approximately at 78 % of every cycle. It is also evident that there is a strong cycle-to-cycle variability caused by the transitional nature of the flow; the latter is characterized by explosive bursts of turbulence, produced during the flow decelerations, separated by turbulence decay phases during the quiescent parts of the cycle (Fortini et al.
Reference Fortini, Espa, Querzoli and Cenedese2015). Another important feature evidenced by figure 17(a) is the very different mobilities of the anterior and posterior leaflets: although both of them are made of the same tissue and have the same thickness, their different curvatures and shapes make the posterior leaflet stiffer, and this is evidenced by the reduced vertical excursion,
![]() $\overline{Z}_{l}$
, during the cycle with respect to the anterior one. Similar dynamics is observed also for the mean horizontal coordinate,
$\overline{Z}_{l}$
, during the cycle with respect to the anterior one. Similar dynamics is observed also for the mean horizontal coordinate,
![]() $\overline{X}_{l}$
, not shown here for the sake of brevity. It is worth mentioning that this effect is independent of the chordae tendinae, which, in the real heart, connect the edges of both leaflets to the myocardium through the papillary muscle. The cordae, in fact, only act at the end of the closing phase by exerting a tension that prevents the leaflets from everting into the mitral channel. The kinematic effect of the chordae tendinae has been modelled in our numerical simulation by freezing the vertical dynamics of the leaflets during the systole once the valve has closed.
$\overline{X}_{l}$
, not shown here for the sake of brevity. It is worth mentioning that this effect is independent of the chordae tendinae, which, in the real heart, connect the edges of both leaflets to the myocardium through the papillary muscle. The cordae, in fact, only act at the end of the closing phase by exerting a tension that prevents the leaflets from everting into the mitral channel. The kinematic effect of the chordae tendinae has been modelled in our numerical simulation by freezing the vertical dynamics of the leaflets during the systole once the valve has closed.
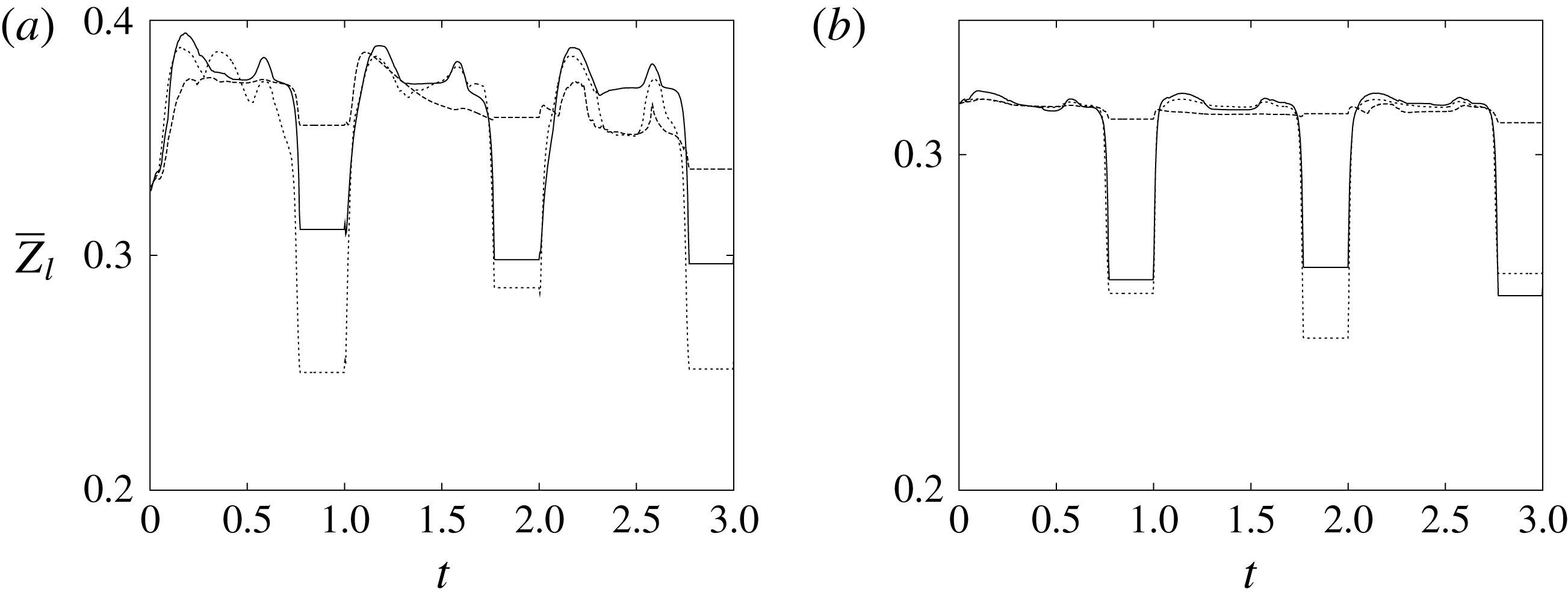
Figure 17. The time evolution of the mean vertical coordinate
![]() $\overline{Z}_{l}$
of the anterior (a) and posterior (b) leaflets of the natural mitral valve: ——,
$\overline{Z}_{l}$
of the anterior (a) and posterior (b) leaflets of the natural mitral valve: ——,
![]() $EF=60\,\%$
; – – – –,
$EF=60\,\%$
; – – – –,
![]() $EF=40\,\%$
;
$EF=40\,\%$
;
![]() $\cdots \cdots$
,
$\cdots \cdots$
,
![]() $EF=60\,\%$
and non-Newtonian fluid model.
$EF=60\,\%$
and non-Newtonian fluid model.
3.2 Healthy ventricle with natural valve and non-Newtonian fluid model
In this section, we briefly report the results obtained for the same configuration as in the previous section (
![]() $EF=60\,\%$
and natural valve) but for a non-Newtonian shear-thinning fluid. The comparison between the two cases is shown in figures 16–18, confirming that, both globally and locally, the differences are minor and very likely due to cycle-to-cycle variation or marginal time convergence of the local phase-averaged statistics. In particular, the dynamics of the valve leaflets as well as the kinetic energy of the flow hardly show any difference, while the mitral jet at the peak of the E-wave (figure 18
a) looks slightly more compact than its Newtonian counterpart (figure 13
b). The effect on the velocity magnitude at the apex probe is to maintain the peak value for a slightly longer time (figure 16
a) even if the features of ventricular flow have very similar cycle evolution. A similar conclusion had been drawn in De Vita et al. (Reference De Vita, de Tullio and Verzicco2016) for the flow through a mechanical bileaflet valve in a realistic aortic root. In that study, the large-scale dynamics of the flow was found to be independent of the fluid model, and the only feature that showed appreciable sensitivity was the haemolysis, which turned out to be approximately 15 % larger for the shear-thinning fluid than for the Newtonian one.
$EF=60\,\%$
and natural valve) but for a non-Newtonian shear-thinning fluid. The comparison between the two cases is shown in figures 16–18, confirming that, both globally and locally, the differences are minor and very likely due to cycle-to-cycle variation or marginal time convergence of the local phase-averaged statistics. In particular, the dynamics of the valve leaflets as well as the kinetic energy of the flow hardly show any difference, while the mitral jet at the peak of the E-wave (figure 18
a) looks slightly more compact than its Newtonian counterpart (figure 13
b). The effect on the velocity magnitude at the apex probe is to maintain the peak value for a slightly longer time (figure 16
a) even if the features of ventricular flow have very similar cycle evolution. A similar conclusion had been drawn in De Vita et al. (Reference De Vita, de Tullio and Verzicco2016) for the flow through a mechanical bileaflet valve in a realistic aortic root. In that study, the large-scale dynamics of the flow was found to be independent of the fluid model, and the only feature that showed appreciable sensitivity was the haemolysis, which turned out to be approximately 15 % larger for the shear-thinning fluid than for the Newtonian one.

Figure 18. The same as figure 13 but for the non-Newtonian fluid model: (a) peak of the E-wave; (b) early systole phase.
3.3 Healthy ventricle with stiffened or stenotic natural valve
As mentioned previously, the membrane mechanical properties in the numerical simulations have been taken from a companion experiment in which a two-component transparent silicone rubber was used to realize the ventricles and the natural valve. This material is linear elastic and isotropic, and therefore totally different from biological tissues which are normally hyperelastic and anisotropic (usually orthotropic, depending on the orientation of the fibres). We believe that this difference is not very important for the ventricle since its volume evolution in time depends on a flow rate that is prescribed as a boundary condition and is therefore independent of the structure dynamics (figure 4). The situation is more delicate for the valves, whose dynamics are determined by the FSI and, thus, by the mechanical properties of the leaflets. Since in this paper we aim to study the flow changes induced by different mitral valves, it is crucial to separate the effects of the deliberately modified geometry from those of the less known material properties. In order to assess the effects of the latter factor, we have run an additional simulation identical to the reference case of § 3.1 but with the thickness of the mitral leaflets doubled (from 0.1 to 0.2) and considering a higher elastic constant for the material (three times larger than the one of the reference case). The results of figures 19–21 show that the solution is relatively insensitive to the specific leaflet properties, at least for the range of parameters explored here. This is true for the global integral quantities, like the flow kinetic energy (figure 21
c), and for the more local ones, like the lateral displacement of the leaflets (figure 21
d) and the pressure drop across the valve (figure 20
a,b). Although at a first glance this insensitivity might seem surprising, it can be easily estimated that for a rectangular (
![]() $a\times b$
) membrane of thickness
$a\times b$
) membrane of thickness
![]() $s$
of density approximately equal to that of the ambient fluid, the added mass overcomes the membrane mass for
$s$
of density approximately equal to that of the ambient fluid, the added mass overcomes the membrane mass for
![]() $s<4b/10$
. On the other hand, the external pressure moments exceed the internal structural reaction for
$s<4b/10$
. On the other hand, the external pressure moments exceed the internal structural reaction for
![]() $s<(5\unicode[STIX]{x0394}pa^{2}b/E)^{1/3}$
, with
$s<(5\unicode[STIX]{x0394}pa^{2}b/E)^{1/3}$
, with
![]() $\unicode[STIX]{x0394}p$
the maximum pressure difference in the fluid. Since in these membranes it results that
$\unicode[STIX]{x0394}p$
the maximum pressure difference in the fluid. Since in these membranes it results that
![]() $s\ll a,b$
and the elastic constant is at most one order of magnitude larger than the pressure difference (
$s\ll a,b$
and the elastic constant is at most one order of magnitude larger than the pressure difference (
![]() $E\approx 2\times 10^{5}$
Pa and
$E\approx 2\times 10^{5}$
Pa and
![]() $\unicode[STIX]{x0394}p\approx 2\times 10^{4}$
Pa for the human mitral valve), the above conditions are always satisfied and the leaflet dynamics is determined mainly by the external loads and the added mass rather than from the specific material properties.
$\unicode[STIX]{x0394}p\approx 2\times 10^{4}$
Pa for the human mitral valve), the above conditions are always satisfied and the leaflet dynamics is determined mainly by the external loads and the added mass rather than from the specific material properties.

Figure 19. The same as figure 13 at the peak of the E-wave for (a) a stiffened natural valve (b) a stenotic natural valve.
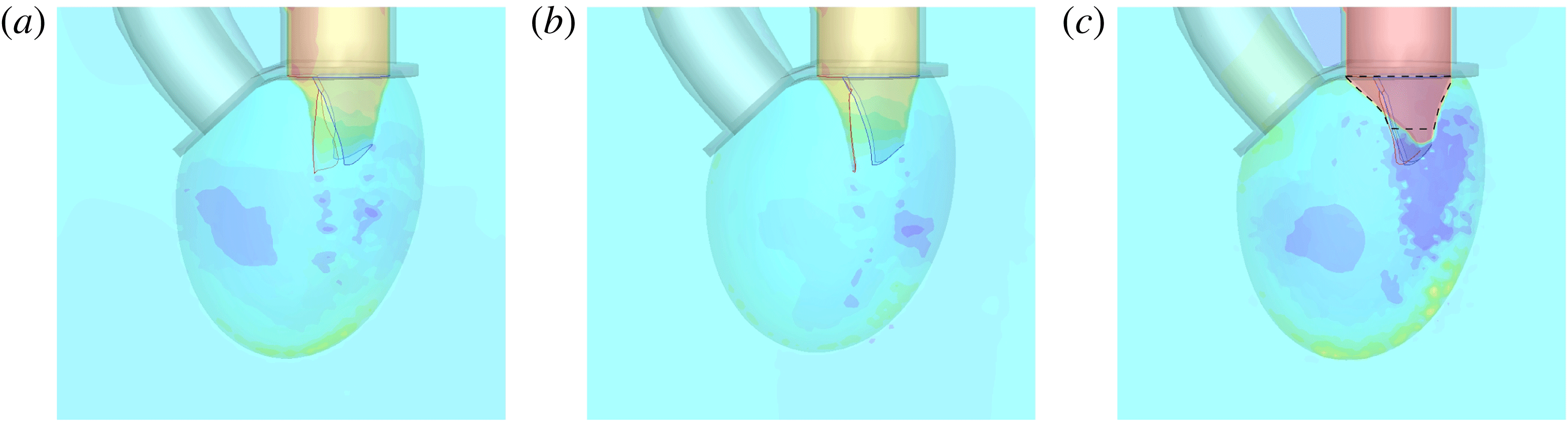
Figure 20. Instantaneous snapshots of the pressure field at the peak of the E-wave (
![]() $EF=60\,\%$
) for (a) a physiological natural valve, (b) a stiffened natural valve and (c) a stenotic natural valve. The dashed line highlights the region where the valve is forced to maintain a fixed geometry in order to mimic the stenosis. The colours range from dark blue,
$EF=60\,\%$
) for (a) a physiological natural valve, (b) a stiffened natural valve and (c) a stenotic natural valve. The dashed line highlights the region where the valve is forced to maintain a fixed geometry in order to mimic the stenosis. The colours range from dark blue,
![]() $p_{min}=-1.5$
, to purple,
$p_{min}=-1.5$
, to purple,
![]() $p_{Max}=2$
.
$p_{Max}=2$
.
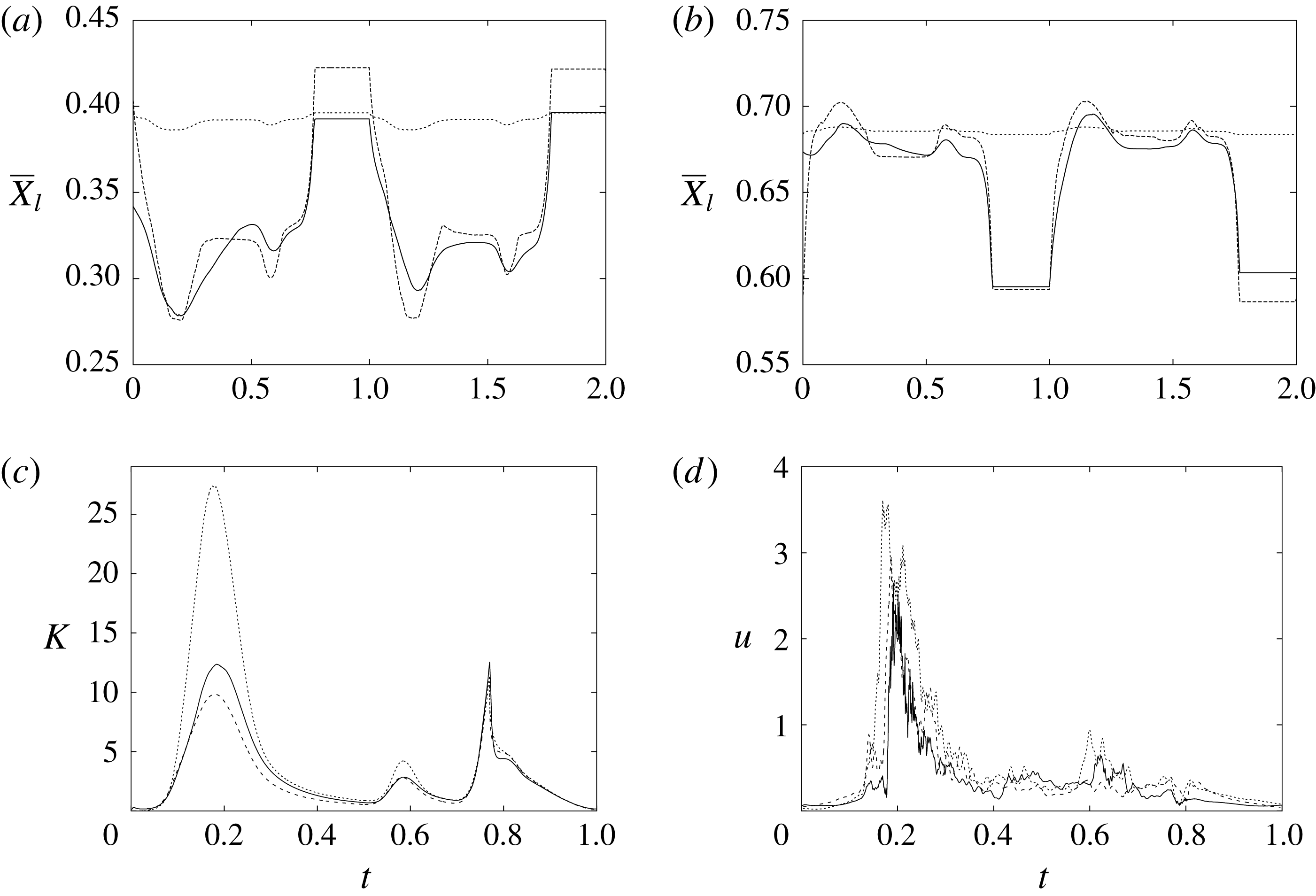
Figure 21. (a) Instantaneous mean
![]() $x$
position of the anterior mitral valve leaflet. (b) The same as (a) but for the posterior leaflet. (c) The phase-averaged kinetic energy of the flow inside the left ventricle. (d) The phase-averaged velocity magnitude at the apex probe. Curves: ——, physiological natural valve; – – – –, stiffened valve; — ⋅ —, stenotic valve.
$x$
position of the anterior mitral valve leaflet. (b) The same as (a) but for the posterior leaflet. (c) The phase-averaged kinetic energy of the flow inside the left ventricle. (d) The phase-averaged velocity magnitude at the apex probe. Curves: ——, physiological natural valve; – – – –, stiffened valve; — ⋅ —, stenotic valve.
A further quantitative measure of the small sensitivity of the solution to the specific properties of the valve leaflets is given by the mean transvalvular pressure drop, which is
![]() $\unicode[STIX]{x0394}p\simeq 0.49$
and
$\unicode[STIX]{x0394}p\simeq 0.49$
and
![]() $\simeq 0.45$
(3.66 and 3.38 mmHg) respectively for the reference and ‘stiffened’ mitral valves.
$\simeq 0.45$
(3.66 and 3.38 mmHg) respectively for the reference and ‘stiffened’ mitral valves.
A more relevant parameter for this problem is instead how the valve leaflets are connected (constrained) to the structure. In the physiological condition, the deformable leaflets are attached to a fibrous ring that behaves very much like a rigid frame, although it changes shape slightly during the heartbeat (Votta et al.
Reference Votta, Caiani, Veronesi, Soncini, Montevecchi and Redaelli2008) (see also the discussion in § 5). For the prosthetic valves, the conditions can vary since there are models (stented) in which the leaflets are connected to a rigid or flexible frame, while in other models (stentless) there is no frame and the leaflets are stitched directly to the fibrous ring. Other pathologic constraints may be present in the natural and prosthetic valves because of calcification that occurs at the junction between the leaflets and the fibrous ring: the progressive growth of the calcium deposit reduces the section available to the flow and limits the mobility of the leaflets (valve stenosis). For all of the simulations, we have constrained the leaflets to the frame (the red structure in figure 3) by fixing the position of the triangle edges crossing the rigid plate. Therefore, regardless of the specific valve type, in all of the cases the lumen of the mitral channel is the same. In order to test the effects of more constrained leaflets or the occurrence of stenotic conditions, we have simulated a case in which the motion of the leaflets within the dashed line of figure 20(c) (
![]() $z<0.5$
) was prevented, with the area of the mitral channel reduced by 72 %. Figures 19–21 indicate that relevant changes are produced in the flow, and the limited mobility of the leaflets is accompanied by a higher velocity of the mitral jet (given the imposed constant flow rate), which in turn produces higher kinetic energy of the ventricular flow. The faster jet, however, is not as efficient as the physiological one since, while its velocity is
$z<0.5$
) was prevented, with the area of the mitral channel reduced by 72 %. Figures 19–21 indicate that relevant changes are produced in the flow, and the limited mobility of the leaflets is accompanied by a higher velocity of the mitral jet (given the imposed constant flow rate), which in turn produces higher kinetic energy of the ventricular flow. The faster jet, however, is not as efficient as the physiological one since, while its velocity is
![]() ${\approx}3.4$
times larger than the reference case, the apex peak velocity is only
${\approx}3.4$
times larger than the reference case, the apex peak velocity is only
![]() ${\approx}16\,\%$
more intense (figure 21
d). On the other hand, the stenosis generates a larger pressure drop across the valve (figure 20
c), whose mean value is
${\approx}16\,\%$
more intense (figure 21
d). On the other hand, the stenosis generates a larger pressure drop across the valve (figure 20
c), whose mean value is
![]() $\unicode[STIX]{x0394}p\simeq 3.05$
(
$\unicode[STIX]{x0394}p\simeq 3.05$
(
![]() $22.93$
mmHg), much larger than the
$22.93$
mmHg), much larger than the
![]() $\unicode[STIX]{x0394}p\approx 0.5$
obtained for the above valves with full mobility.
$\unicode[STIX]{x0394}p\approx 0.5$
obtained for the above valves with full mobility.
It should be pointed out, however, that, while the described trends are general, the specific values depend heavily on the detailed geometry of the obstruction (calcification), which not only may reduce the available area but also may induce asymmetries.
3.4 Pathological ventricle with natural valve
In order to isolate the effect of a reduced ejection fraction, here we consider the same case as in § 3.1 except for the ejection fraction, which is reduced to the lower end of the pathological value,
![]() $EF=40\,\%$
. Comparison between the panels of figures 13 and 22 immediately evidences the weakened flow within the ventricle, which, however, can still reach the apex of the ventricle and ‘wash’ that region. A similar picture emerges from the apex probe in figure 16(a) and the kinetic energy in figure 16(b). An important difference from the case at
$EF=40\,\%$
. Comparison between the panels of figures 13 and 22 immediately evidences the weakened flow within the ventricle, which, however, can still reach the apex of the ventricle and ‘wash’ that region. A similar picture emerges from the apex probe in figure 16(a) and the kinetic energy in figure 16(b). An important difference from the case at
![]() $EF=60\,\%$
is that now the recirculation dies out during the diastasis. Therefore, the A-wave, rather than reinforcing the vortex previously generated by the E-wave, produces a new weaker recirculation that is expelled from the ventricle during the systole. The time evolution of the leaflet motion of figure 17(b) is consistent with the described picture: again, the posterior leaflet moves less than the anterior one and there is some cycle-to-cycle variability. In this case, however, the displacements are quite small and the reduced momentum of the mitral jet is not enough to open the valve completely. From a comparison of figures 13(e) and 22(b), we note that, in this case, the weak contraction of the ventricle during systole can still close the valve although it does not squeeze the leaflets one against the other; this could cause some valve leakage, known as mitral insufficiency. Phase-averaged profiles, as in figures 14 and 15, not reported here for the sake of brevity, show a similar behaviour to that in the case of § 3.1 although with reduced amplitude for the mean and r.m.s. velocity profiles. The smaller amplitude of the fluctuations is consistent with the fact that an ejection fraction of
$EF=60\,\%$
is that now the recirculation dies out during the diastasis. Therefore, the A-wave, rather than reinforcing the vortex previously generated by the E-wave, produces a new weaker recirculation that is expelled from the ventricle during the systole. The time evolution of the leaflet motion of figure 17(b) is consistent with the described picture: again, the posterior leaflet moves less than the anterior one and there is some cycle-to-cycle variability. In this case, however, the displacements are quite small and the reduced momentum of the mitral jet is not enough to open the valve completely. From a comparison of figures 13(e) and 22(b), we note that, in this case, the weak contraction of the ventricle during systole can still close the valve although it does not squeeze the leaflets one against the other; this could cause some valve leakage, known as mitral insufficiency. Phase-averaged profiles, as in figures 14 and 15, not reported here for the sake of brevity, show a similar behaviour to that in the case of § 3.1 although with reduced amplitude for the mean and r.m.s. velocity profiles. The smaller amplitude of the fluctuations is consistent with the fact that an ejection fraction of
![]() $EF=40\,\%$
yields a peak Reynolds number that is approximately half of that in the case of
$EF=40\,\%$
yields a peak Reynolds number that is approximately half of that in the case of
![]() $EF=60\,\%$
(see the curves of figure 12).
$EF=60\,\%$
(see the curves of figure 12).

Figure 22. The same as figure 13 but for
![]() $EF=40\,\%$
: (a) early phase of E-wave; (b) early systole phase.
$EF=40\,\%$
: (a) early phase of E-wave; (b) early systole phase.

Figure 23. Snapshots of the three different mitral valves, natural (a,d), biological (b,e) and mechanical (c,f), in fully open and closed positions in the case of a healthy left ventricle (
![]() $EF=60\,\%$
).
$EF=60\,\%$
).
3.5 Ventricle with mechanical bileaflet valve
As mentioned above, if the mitral valve has to be replaced, and the life expectation of the patient is more than 15 years, the most common choice is a mechanical bileaflet valve. The kinematics of this prosthesis is such that the leaflets always occupy part of the mitral channel, even when the valve is fully open (figure 23
c), and this is a crucial difference with respect to the natural and biological prosthetic valves in which the flow pushes the flexible leaflets towards the channel boundary leaving the orifice completely clear (figure 23
a,b). The problem is further exacerbated by the necessity of giving the rigid leaflets in the fully open position an inclination (
![]() ${\approx}10^{\circ }$
) in order for the incipient reverse flow to generate a moment closing the valve. This yields the poor haemodynamics of the prosthesis, with an increased turbulence level downstream of the valve. This produces augmented mechanical stresses on the corpuscular part of the blood which cause red blood cell damage (haemolysis) and platelet activation (Grigioni et al.
Reference Grigioni, Daniele, D’Avenio and Barbaro2001). These phenomena both contribute to the formation of clots, whose aggregation is countered by a lifelong anticoagulant therapy, which, in turn, increases the risks of bleeding and haemorrhagic events.
${\approx}10^{\circ }$
) in order for the incipient reverse flow to generate a moment closing the valve. This yields the poor haemodynamics of the prosthesis, with an increased turbulence level downstream of the valve. This produces augmented mechanical stresses on the corpuscular part of the blood which cause red blood cell damage (haemolysis) and platelet activation (Grigioni et al.
Reference Grigioni, Daniele, D’Avenio and Barbaro2001). These phenomena both contribute to the formation of clots, whose aggregation is countered by a lifelong anticoagulant therapy, which, in turn, increases the risks of bleeding and haemorrhagic events.
The altered flow dynamics is shown in figure 24 for an ejection fraction
![]() $EF=60\,\%$
, which models a healthy ventricle. It is evident that the mitral jet during the E-wave is much less regular and smooth with respect to the analogous field in figure 13(a), and the augmented turbulence enhances the lateral spreading of the jet to the detriment of its vertical penetration. A more quantitative view of this phenomenon can be obtained by the time evolution of the phase-averaged velocity magnitude at the apex probe (figure 25
a), showing a strongly fluctuating signal with a mean component that is much weaker than in the case of the natural valve (figure 16
a). Another important difference is that the mitral jet, which has lost part of its momentum into small-scale fluctuations, generates a weak large-scale recirculation whose intensity hardly lasts up to the A-wave, as confirmed by the velocity signal during the diastasis which decreases continuously. The A-wave, on the other hand, undergoes a dynamics similar to that previously described, but now, being weaker, produces an effect at the ventricle apex of the same order as the underlying velocity fluctuations. This picture is confirmed by the evolution of the kinetic energy of the flow within the ventricle, evidencing a less energetic flow throughout the cycle (figure 25
b).
$EF=60\,\%$
, which models a healthy ventricle. It is evident that the mitral jet during the E-wave is much less regular and smooth with respect to the analogous field in figure 13(a), and the augmented turbulence enhances the lateral spreading of the jet to the detriment of its vertical penetration. A more quantitative view of this phenomenon can be obtained by the time evolution of the phase-averaged velocity magnitude at the apex probe (figure 25
a), showing a strongly fluctuating signal with a mean component that is much weaker than in the case of the natural valve (figure 16
a). Another important difference is that the mitral jet, which has lost part of its momentum into small-scale fluctuations, generates a weak large-scale recirculation whose intensity hardly lasts up to the A-wave, as confirmed by the velocity signal during the diastasis which decreases continuously. The A-wave, on the other hand, undergoes a dynamics similar to that previously described, but now, being weaker, produces an effect at the ventricle apex of the same order as the underlying velocity fluctuations. This picture is confirmed by the evolution of the kinetic energy of the flow within the ventricle, evidencing a less energetic flow throughout the cycle (figure 25
b).

Figure 24. The same as figure 13 but for a mechanical valve at
![]() $EF=60\,\%$
: (a) early phase of E-wave; (b) early systole phase.
$EF=60\,\%$
: (a) early phase of E-wave; (b) early systole phase.
The velocity profiles of figures 14 and 15 reinforce the analysis made above. In particular, figure 14(a) evidences the typical three-jet configuration of the mean flow whose peak velocity is the smallest among all valves. As the flow rate is identical for all of the valves (and is imposed as a boundary condition), a smaller peak velocity suggests a larger lateral spreading and a weaker ventricular recirculation, as indicated by the small amplitude of the negative velocity. The same dynamics is observed farther downstream in figure 15(a,c) (
![]() $z=2$
), with the mean flow still maintaining more than one peak and the vanishing ventricular recirculation.
$z=2$
), with the mean flow still maintaining more than one peak and the vanishing ventricular recirculation.
The dynamics during the A-wave (figures 14 b,d and 15 b,d) partly benefits from the fact that, differently from the natural and biological valves, the leaflets remain in the fully open position during all of the diastole and no inflow momentum is used for the valve opening. Nevertheless, the disturbances of the leaflets on the ventricular flow are still visible from the highest level of fluctuations in figure 14(d) and the weakest mean and r.m.s. flow shown in figure 15(b,d).
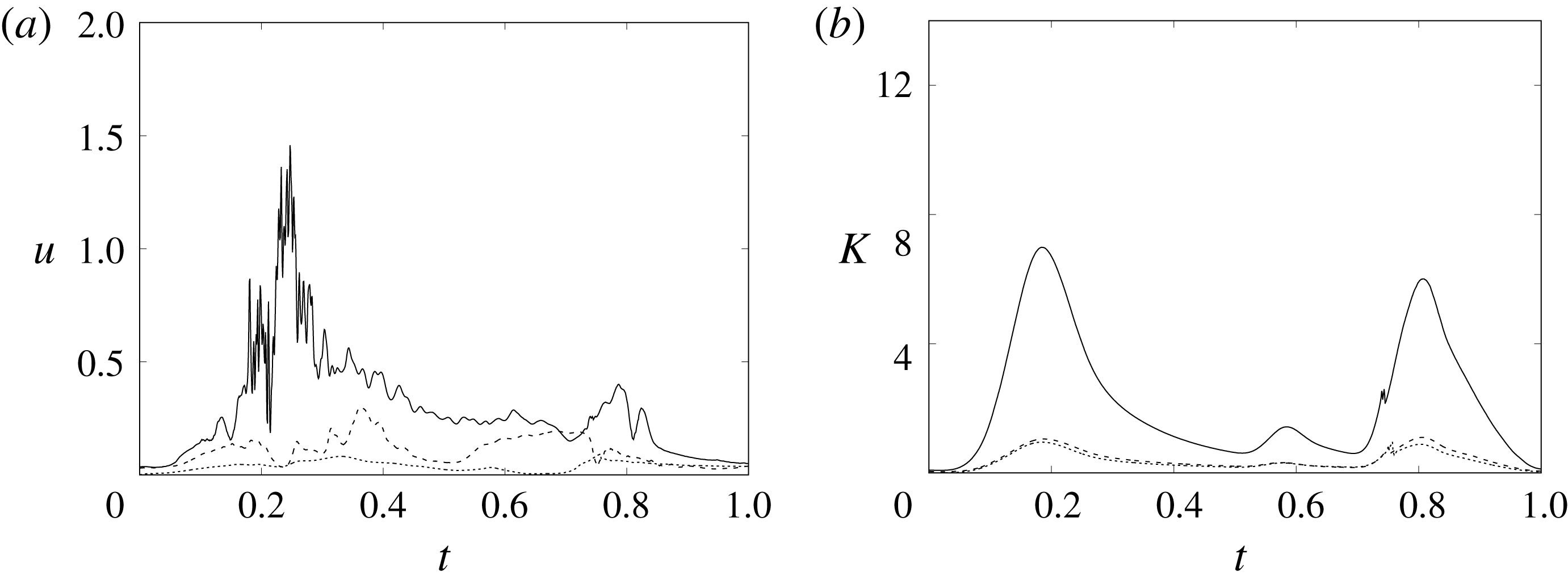
Figure 25. The same as figure 16 but for a mechanical valve. Curves: ——,
![]() $EF=60\,\%$
; – – – –,
$EF=60\,\%$
; – – – –,
![]() $EF=40\,\%$
;
$EF=40\,\%$
;
![]() $\cdots \cdots$
,
$\cdots \cdots$
,
![]() $EF=40\,\%$
and the valve in the anti-anatomical position.
$EF=40\,\%$
and the valve in the anti-anatomical position.

Figure 26. The same as figure 13 but for a mechanical valve at
![]() $EF=40\,\%$
: (a) early phase of E-wave; (b) early systole phase.
$EF=40\,\%$
: (a) early phase of E-wave; (b) early systole phase.
The above scenario considerably worsens if the pumping efficiency of the ventricle drops below the healthy range. In this paper, we have considered the case at
![]() $EF=40\,\%$
, the results of which are reported in figures 25–26. The dynamics is similar to the case at
$EF=40\,\%$
, the results of which are reported in figures 25–26. The dynamics is similar to the case at
![]() $EF=60\,\%$
, with the fundamental difference that now the reduced momentum of the inflow, combined with the perturbations introduced by the valve leaflets, further decreases the penetration capability of the mitral jet and produces a stagnant fluid region at the ventricle apex. This is quantitatively confirmed by the velocity sampled at the apex probe, which shows negligible values over the whole cycle, and by the time evolution of the flow kinetic energy (figure 25
b), which results to be at least two times lower than the analogous flow with the natural valve.
$EF=60\,\%$
, with the fundamental difference that now the reduced momentum of the inflow, combined with the perturbations introduced by the valve leaflets, further decreases the penetration capability of the mitral jet and produces a stagnant fluid region at the ventricle apex. This is quantitatively confirmed by the velocity sampled at the apex probe, which shows negligible values over the whole cycle, and by the time evolution of the flow kinetic energy (figure 25
b), which results to be at least two times lower than the analogous flow with the natural valve.
In some studies (Machler et al.
Reference Machler, Perthel, Reiter, Reiter, Zink, Bergmann, Waltensdorfer and Laas2004; Choi, Vedula & Mittal Reference Choi, Vedula and Mittal2014), it has been investigated whether implantation of the mechanical valve in the ‘anti-anatomical’ position, i.e. with the leaflets orthogonal with respect to the natural configuration, could give better haemodynamics with respect to the latter implantation. This issue has been the subject of many discussions among cardiac surgeons and clear evidence of an advantage has not emerged. Here, we have simulated the anti-anatomical configuration in the case of a ventricle at
![]() $EF=40\,\%$
, the critical case that would benefit most from some improvements. We have found that, consistently with the available literature, no appreciable differences are observed with respect to the standard case. In fact, apart from the obvious different orientation of the jet leaving the valve, the velocity magnitude at the apex probe is even smaller than in the case of anatomical implantation, as observed by Choi et al. (Reference Choi, Vedula and Mittal2014). Anyway, the flow velocity at the apex remains negligible during all of the cycle and also the kinetic energy of the ventricular flow is essentially the same as in the original case (figure 25).
$EF=40\,\%$
, the critical case that would benefit most from some improvements. We have found that, consistently with the available literature, no appreciable differences are observed with respect to the standard case. In fact, apart from the obvious different orientation of the jet leaving the valve, the velocity magnitude at the apex probe is even smaller than in the case of anatomical implantation, as observed by Choi et al. (Reference Choi, Vedula and Mittal2014). Anyway, the flow velocity at the apex remains negligible during all of the cycle and also the kinetic energy of the ventricular flow is essentially the same as in the original case (figure 25).
3.6 Ventricle with biological valve
The same simulations as in the previous sections are repeated here with a trileaflet biological prosthesis, like that of figure 2(b), in the mitral position. As shown in figure 23, when this valve opens, the lumen remains free from obstacles and the mitral jet enters the ventricle as a compact vertical stream capable of penetrating the ventricle volume up to the apex. However, since the three leaflets are all identical, they open in a nearly symmetrical way and the emerging jet always points vertically downward during all of the E-wave injection (figure 27 a). This is a relevant difference from the natural valve, which, due to the leaflet asymmetry, initially produces a jet pointing laterally to the sidewall (figure 24 a) and only at the peak of the E-wave is bent vertically (figure 24 b) and directed towards the ventricle apex.
The fact that, with a trileaflet valve, the mitral jet constantly points towards the ventricle apex is further confirmed by looking at figures 16(a) and 29(a): although in both cases the inflow is the same (
![]() $EF=60\,\%$
of figure 12), the peak velocity at the apex probe occurs earlier for the prosthetic than for the natural valve. Comparing these results with those of the mechanical valve (figure 25
a), it is evident that the haemodynamic performance of the biological valve is better than that of the mechanical prosthesis, although both of them produce strong enough recirculations to avoid ventricular haemostasis during the diastolic part of the cycle.
$EF=60\,\%$
of figure 12), the peak velocity at the apex probe occurs earlier for the prosthetic than for the natural valve. Comparing these results with those of the mechanical valve (figure 25
a), it is evident that the haemodynamic performance of the biological valve is better than that of the mechanical prosthesis, although both of them produce strong enough recirculations to avoid ventricular haemostasis during the diastolic part of the cycle.
For the present trileaflet valve, the velocity profiles of figures 14 and 15 show flow features that are comparable to those of the natural valve and with a definitely better haemodynamics than that of the mechanical prosthesis. In more detail, the present valve can produce relatively compact mitral jets capable of penetrating the ventricle up to the apex and generating the beneficial recirculation (figures 14 a and 15 a,b) that prevents the haemostasis. This suggests that the biological valve might operate adequately even in an impaired ventricle with a reduced ejection fraction generating low-momentum mitral jets.

Figure 27. The same as figure 24 but for a biological valve at
![]() $EF=60\,\%$
: (a) early phase of E-wave; (b) early systole phase.
$EF=60\,\%$
: (a) early phase of E-wave; (b) early systole phase.

Figure 28. The same as figure 27 but for
![]() $EF=40\,\%$
: (a) early phase of E-wave; (b) early systole phase.
$EF=40\,\%$
: (a) early phase of E-wave; (b) early systole phase.
In fact, when a mitral biological valve is combined with a pathologic ventricle (
![]() $EF=40\,\%$
), the superiority with respect to the mechanical valve is amplified and, differently from the latter, the former still operates correctly with a haemodynamics similar to the natural one. As shown in figure 28(a), although the mitral jet has a reduced momentum, the ventricular recirculation still extends up to the apex and the peak of the E-wave has a distinct signature in the probe signal (figure 29
a).
$EF=40\,\%$
), the superiority with respect to the mechanical valve is amplified and, differently from the latter, the former still operates correctly with a haemodynamics similar to the natural one. As shown in figure 28(a), although the mitral jet has a reduced momentum, the ventricular recirculation still extends up to the apex and the peak of the E-wave has a distinct signature in the probe signal (figure 29
a).
The time histories of the ventricular kinetic energy (figures 16 b, 25 b and 29 b) tell a similar story with the biological prosthesis, which outperforms the mechanical one for all ejection fractions. It is, however, well known that the better haemodynamics of biological valves comes at the price of a durability of the order of 15–20 years, to be compared with a lifetime of 80 years for the mechanical devices (Hoffmann, Lutter & Cremer Reference Hoffmann, Lutter and Cremer2008).
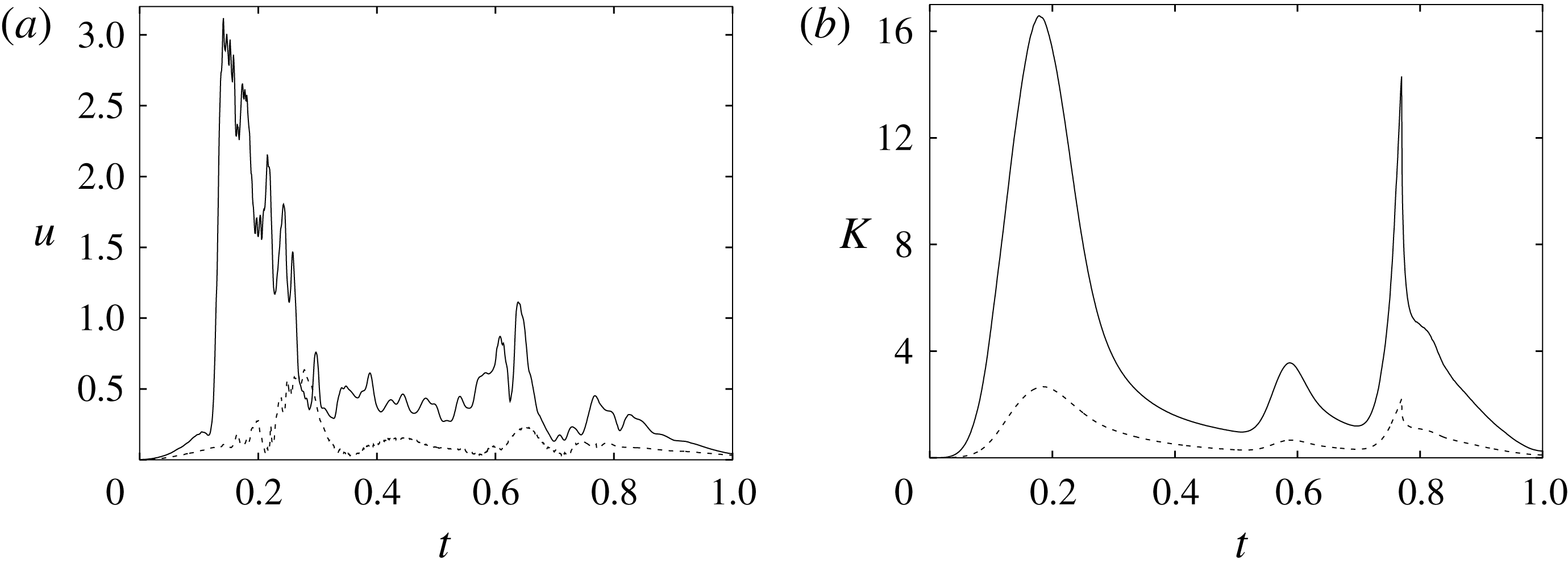
Figure 29. The same as figure 16 but for a biological valve. Curves: ——,
![]() $EF=60\,\%$
; – – – –,
$EF=60\,\%$
; – – – –,
![]() $EF=40\,\%$
.
$EF=40\,\%$
.

Figure 30. Streamtraces in the
![]() $x$
–
$x$
–
![]() $z$
symmetry plane at the end of the diastole (
$z$
symmetry plane at the end of the diastole (
![]() $t=0.69$
) for
$t=0.69$
) for
![]() $EF=40\,\%$
: (a) natural valve; (b) biological valve; (c) mechanical valve.
$EF=40\,\%$
: (a) natural valve; (b) biological valve; (c) mechanical valve.
4 Discussion
The main finding of this investigation is summarized by the snapshots of figure 30, showing the streamtraces in the
![]() $x$
–
$x$
–
![]() $z$
symmetry plane at the end of the diastole (
$z$
symmetry plane at the end of the diastole (
![]() $t=0.69$
) when the ventricle attains its maximum volume. All three flows are computed for an ejection fraction of 40 %, an inflow curve like that of figure 12 and for otherwise identical conditions except for the type of mitral valve. It is evident that the large-scale recirculation is strongly determined by the specific valve model, and in the case of a mechanical valve, the large-scale vortex does not reach the ventricle apex. It is worth mentioning that for all of the three cases of figure 30, the E-wave propagation index (EPI) described in Harfi et al. (Reference Harfi, Seo, Yasir, Welsh, Meyer, Abraham, Gerge and Mittal2017) would be nearly identical since it is given by the ratio of the propagation length of the mitral jet,
$t=0.69$
) when the ventricle attains its maximum volume. All three flows are computed for an ejection fraction of 40 %, an inflow curve like that of figure 12 and for otherwise identical conditions except for the type of mitral valve. It is evident that the large-scale recirculation is strongly determined by the specific valve model, and in the case of a mechanical valve, the large-scale vortex does not reach the ventricle apex. It is worth mentioning that for all of the three cases of figure 30, the E-wave propagation index (EPI) described in Harfi et al. (Reference Harfi, Seo, Yasir, Welsh, Meyer, Abraham, Gerge and Mittal2017) would be nearly identical since it is given by the ratio of the propagation length of the mitral jet,
![]() $L_{MJ}$
, and the vertical length of the ventricle at the maximum expansion,
$L_{MJ}$
, and the vertical length of the ventricle at the maximum expansion,
![]() $L_{LV}$
. As shown by Harfi et al. (Reference Harfi, Seo, Yasir, Welsh, Meyer, Abraham, Gerge and Mittal2017), for all practical purposes,
$L_{LV}$
. As shown by Harfi et al. (Reference Harfi, Seo, Yasir, Welsh, Meyer, Abraham, Gerge and Mittal2017), for all practical purposes,
![]() $L_{MJ}$
can be estimated in echocardiography through the velocity time integral
$L_{MJ}$
can be estimated in echocardiography through the velocity time integral
![]() $VTI=\int _{0}^{T_{E}}V_{M}(t)\,\text{d}t$
, where
$VTI=\int _{0}^{T_{E}}V_{M}(t)\,\text{d}t$
, where
![]() $T_{E}$
is the duration of the early wave and
$T_{E}$
is the duration of the early wave and
![]() $V_{M}$
is the jet velocity at the mitral leaflets. Since all of the inflows are identical and
$V_{M}$
is the jet velocity at the mitral leaflets. Since all of the inflows are identical and
![]() $L_{LV}$
depends on the ejection fraction, in all cases, the E-wave propagation index is the same and indeed a direct calculation for
$L_{LV}$
depends on the ejection fraction, in all cases, the E-wave propagation index is the same and indeed a direct calculation for
![]() $EF=40\,\%$
yields
$EF=40\,\%$
yields
![]() $EPI=1.24$
, 1.35 and 1.31 respectively for the natural, biological and mechanical valves.
$EPI=1.24$
, 1.35 and 1.31 respectively for the natural, biological and mechanical valves.
This is fully consistent with the time evolution of the vertical velocity component (as obtained from the mitral probes of figure 3
b) at the centre of the jet and halfway between the mitral leaflets,
![]() $z=0.75$
(figure 32
a), showing a very similar evolution for all mitral valves. On the other hand, the same quantity further downstream at
$z=0.75$
(figure 32
a), showing a very similar evolution for all mitral valves. On the other hand, the same quantity further downstream at
![]() $z=1.5$
(figure 32
b) indicates a different evolution of the mitral jet with the natural valve which produces the largest velocity and the mechanical valve which produces the smallest.
$z=1.5$
(figure 32
b) indicates a different evolution of the mitral jet with the natural valve which produces the largest velocity and the mechanical valve which produces the smallest.
The velocity profiles of figure 32(b) might be more relevant for clinical diagnosis than those of figure 32(a), since in echocardiography the mitral flow Doppler is not measured at the base of the valve but rather at a downstream section. The EPI computed with these profiles yields
![]() $EPI=1.52$
, 1.38 and 0.69 respectively for the natural, biological and mechanical valves, thus confirming all of the discussion of the previous sections.
$EPI=1.52$
, 1.38 and 0.69 respectively for the natural, biological and mechanical valves, thus confirming all of the discussion of the previous sections.
To provide further evidence of the above described dynamics, the wash-out curves for a passive scalar have also been computed. Taking as initial condition a ventricle filled with a scalar at concentration
![]() $q=1$
, the flows have been evolved by injecting ‘clean’ fluid (
$q=1$
, the flows have been evolved by injecting ‘clean’ fluid (
![]() $q=0$
) from the mitral inflow, and a convection/diffusion equation has been integrated using the velocities from the previous numerical simulations and a Schmidt number of
$q=0$
) from the mitral inflow, and a convection/diffusion equation has been integrated using the velocities from the previous numerical simulations and a Schmidt number of
![]() $Sc=1$
. The time evolution of the total scalar
$Sc=1$
. The time evolution of the total scalar
![]() $Q=\int _{V_{v}}q\,\text{d}V$
(where
$Q=\int _{V_{v}}q\,\text{d}V$
(where
![]() $V_{v}$
is the time-dependent ventricle volume) has been computed for all of the cases. It is easy to show that if the inflow did not mix at all and were completely ejected during the systole,
$V_{v}$
is the time-dependent ventricle volume) has been computed for all of the cases. It is easy to show that if the inflow did not mix at all and were completely ejected during the systole,
![]() $Q$
would remain constant throughout the cycle. In contrast, in the case of perfect mixing,
$Q$
would remain constant throughout the cycle. In contrast, in the case of perfect mixing,
![]() $Q$
decreases in a cycle by the same percentage as
$Q$
decreases in a cycle by the same percentage as
![]() $EF$
. In real cases, however, the mixing will never be perfect and the decrease of
$EF$
. In real cases, however, the mixing will never be perfect and the decrease of
![]() $Q$
will depend on the structure of the ventricular flow.
$Q$
will depend on the structure of the ventricular flow.
In figures 31(a,b), instantaneous snapshots of
![]() $q$
are reported for a representative case, showing the incoming jet of the clean fluid that eventually partially mixes with the
$q$
are reported for a representative case, showing the incoming jet of the clean fluid that eventually partially mixes with the
![]() $q$
-concentrated fluid inside the ventricle. During the diastole (figure 31
a), although the mean
$q$
-concentrated fluid inside the ventricle. During the diastole (figure 31
a), although the mean
![]() $q$
concentration decreases, due to the dilution with the clean fluid, the total scalar remains constant. In contrast, during the systole (figure 31
b), the mixed fluid is ejected from the ventricle through the aortic channel and
$q$
concentration decreases, due to the dilution with the clean fluid, the total scalar remains constant. In contrast, during the systole (figure 31
b), the mixed fluid is ejected from the ventricle through the aortic channel and
![]() $Q$
decreases in time. Figure 31(c,d) shows that this behaviour is common to all the mitral valves, although the amount of wash-out is different. This is especially true for the cases at
$Q$
decreases in time. Figure 31(c,d) shows that this behaviour is common to all the mitral valves, although the amount of wash-out is different. This is especially true for the cases at
![]() $EF=40\,\%$
, for which it is confirmed that the mechanical valve produces the minimum ventricle wash-out.
$EF=40\,\%$
, for which it is confirmed that the mechanical valve produces the minimum ventricle wash-out.

Figure 31. (a,b) Instantaneous distribution in the
![]() $x$
–
$x$
–
![]() $z$
symmetry plane of a passive scalar
$z$
symmetry plane of a passive scalar
![]() $q$
for a bileaflet mechanical valve and
$q$
for a bileaflet mechanical valve and
![]() $EF=40\,\%$
: (a) beginning of the systole (
$EF=40\,\%$
: (a) beginning of the systole (
![]() $t=0.1$
); (b) end of the diastole (
$t=0.1$
); (b) end of the diastole (
![]() $t=0.9$
). The colour contours of the passive scalar range from
$t=0.9$
). The colour contours of the passive scalar range from
![]() $q=0$
(blue) to
$q=0$
(blue) to
![]() $q=1$
(red). (c,d) The time evolution of the normalized total scalar
$q=1$
(red). (c,d) The time evolution of the normalized total scalar
![]() $Q/Q_{0}$
during a heartbeat for (c)
$Q/Q_{0}$
during a heartbeat for (c)
![]() $EF=40\,\%$
and (d)
$EF=40\,\%$
and (d)
![]() $EF=60\,\%$
(
$EF=60\,\%$
(
![]() $Q_{0}$
is the initial value of
$Q_{0}$
is the initial value of
![]() $Q$
). Curves: ——, bileaflet mechanical valve; – – – –, biological valve;
$Q$
). Curves: ——, bileaflet mechanical valve; – – – –, biological valve;
![]() $\cdots \cdots$
, natural valve.
$\cdots \cdots$
, natural valve.
The fact that each valve perturbs the mitral jet by a different amount is confirmed also by figure 33, showing the histograms of the peak pressure drops across the valve during the cycle that occurs at the peak of the E-wave. It is evident that the mechanical valve in the fully open position produces the largest pressure losses, which are responsible for the velocity drop observed in figure 32 and for the disintegration of the initially coherent jet into small incoherent flow scales.
A popular quantity used to characterize the valve performance is the effective orifice area (EOA), which, among several definitions, can be computed as the ratio of the peak flow rate to the maximum velocity (averaged over the jet section). The EOA can be interpreted as the minimum cross-section of the mitral jet, which is smaller than the geometric orifice area because of vena contracta. Depending on the flow kinematics, the EOA can be significantly smaller than the lumen of the mitral orifice. For example, in the present case, the lumen area is
![]() $A=\unicode[STIX]{x03C0}/4=0.785$
(
$A=\unicode[STIX]{x03C0}/4=0.785$
(
![]() $4.52~\text{cm}^{2}$
), while
$4.52~\text{cm}^{2}$
), while
![]() $EOA=0.628$
, 0.445 and 0.550 (respectively 3.62, 2.56 and
$EOA=0.628$
, 0.445 and 0.550 (respectively 3.62, 2.56 and
![]() $3.17~\text{cm}^{2}$
) for the natural, biological and mechanical valves. The fact that mechanical valves have EOAs generally larger than biological prostheses is consistent with the clinical literature (Pibarot & Dumesnil Reference Pibarot and Dumesnil2012). This quantity, however, takes into account only the geometry of the valve and the continuity equation. Therefore, it might not be adequate to characterize the dynamic performance of the valves. In fact, the transvalvular pressure drop (referred to as the ‘pressure gradient’ within the clinical community) shown in figure 33(b) does not correlate with the EOA since its value depends also on the balance of momentum in the flow.
$3.17~\text{cm}^{2}$
) for the natural, biological and mechanical valves. The fact that mechanical valves have EOAs generally larger than biological prostheses is consistent with the clinical literature (Pibarot & Dumesnil Reference Pibarot and Dumesnil2012). This quantity, however, takes into account only the geometry of the valve and the continuity equation. Therefore, it might not be adequate to characterize the dynamic performance of the valves. In fact, the transvalvular pressure drop (referred to as the ‘pressure gradient’ within the clinical community) shown in figure 33(b) does not correlate with the EOA since its value depends also on the balance of momentum in the flow.
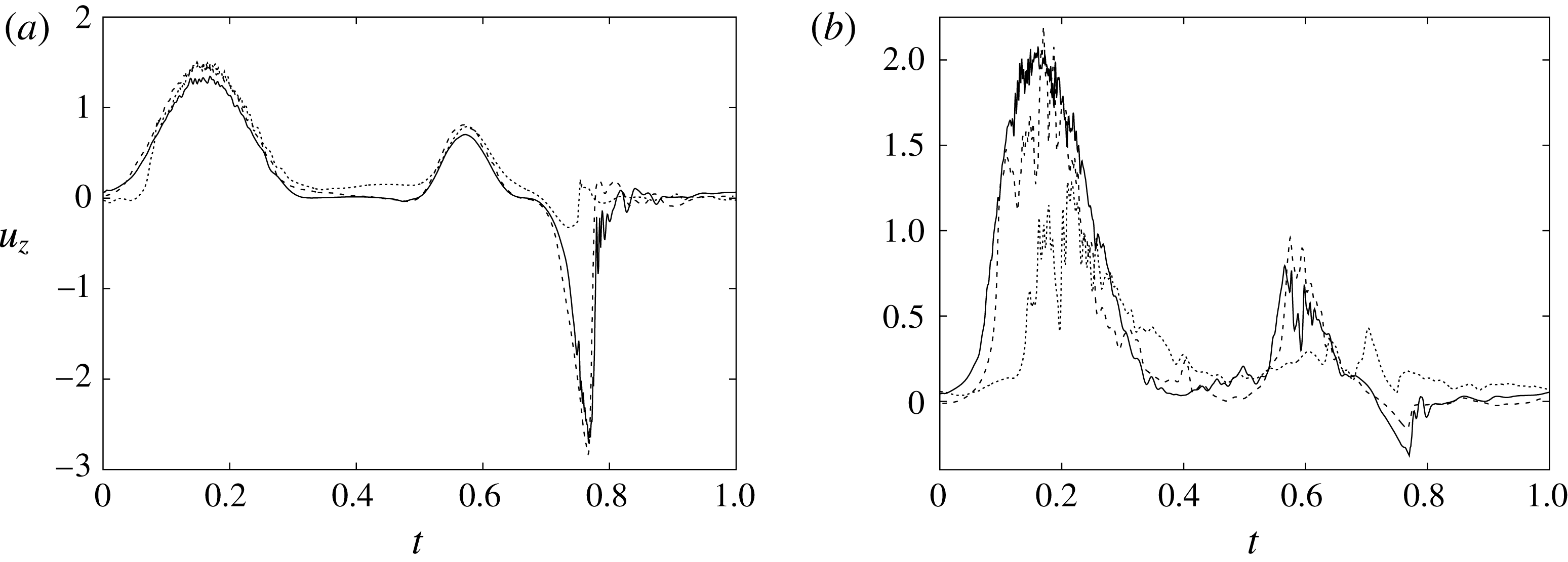
Figure 32. The phase-averaged vertical velocity at the ‘mitral’ probe at
![]() $z=0.75$
(a) and the ‘tip’ probe at
$z=0.75$
(a) and the ‘tip’ probe at
![]() $z=1.5$
(b) for
$z=1.5$
(b) for
![]() $EF=40\,\%$
. Curves: ——, natural valve; – – – –, biological valve;
$EF=40\,\%$
. Curves: ——, natural valve; – – – –, biological valve;
![]() $\cdots \cdots$
, mechanical valve.
$\cdots \cdots$
, mechanical valve.
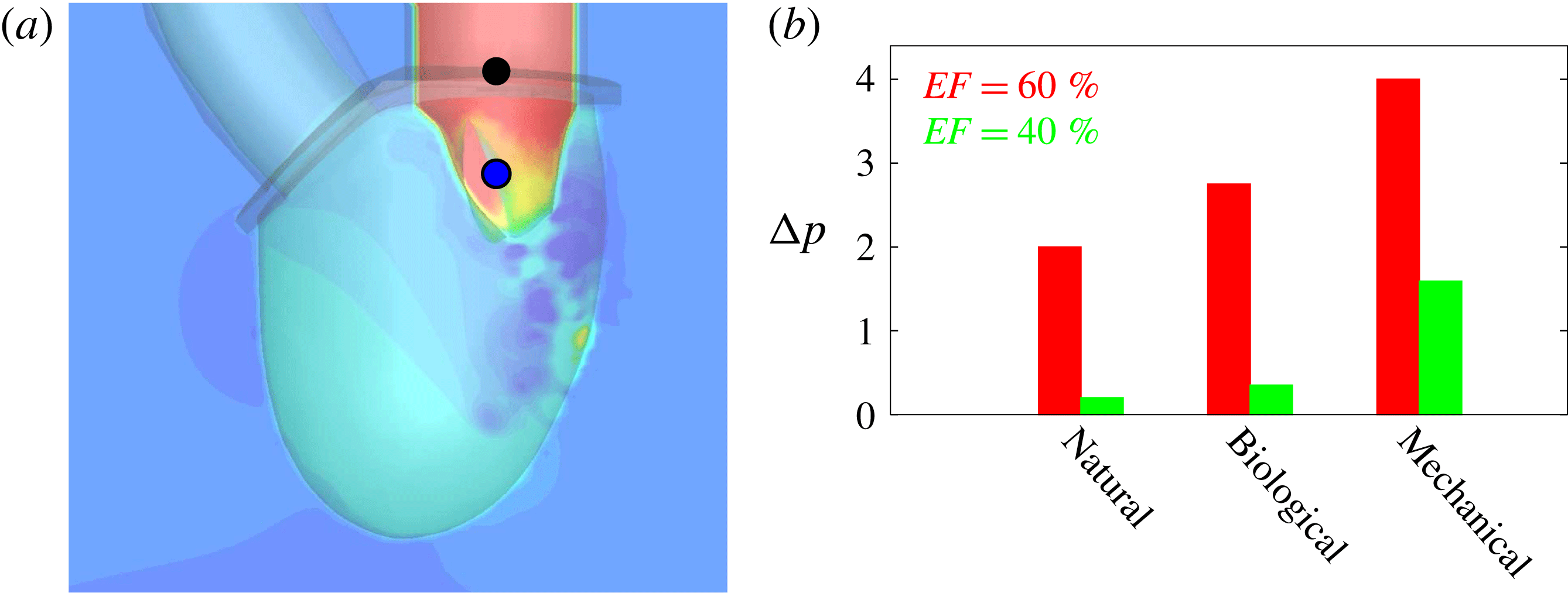
Figure 33. (a) Snapshot of the pressure field values of the left ventricle with a natural mitral valve at early diastole phase. The two bullets indicate the representative positions among which the pressure drop is evaluated. (b) Maximum pressure drops at the peak systole for the natural, biological and mechanical mitral valves in the cases of both
![]() $EF=60\,\%$
and
$EF=60\,\%$
and
![]() $EF=40\,\%$
.
$EF=40\,\%$
.
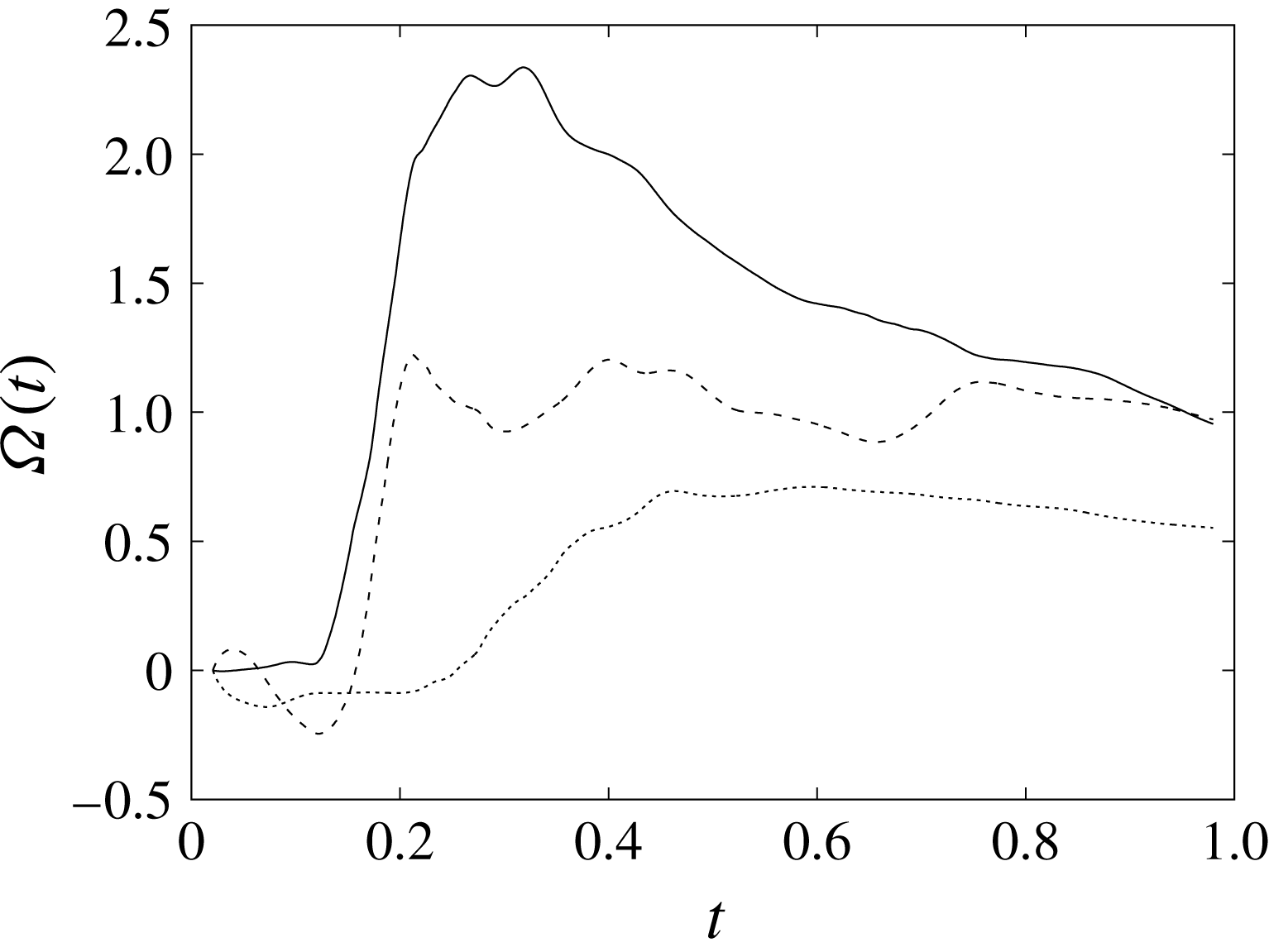
Figure 34. The time evolution of the averaged circulation
![]() $\unicode[STIX]{x1D6FA}(t)$
of the ventricular flow at
$\unicode[STIX]{x1D6FA}(t)$
of the ventricular flow at
![]() $EF=40\,\%$
. Curves: ——, natural valve; – – – –, biological valve;
$EF=40\,\%$
. Curves: ——, natural valve; – – – –, biological valve;
![]() $\cdots \cdots$
, mechanical valve.
$\cdots \cdots$
, mechanical valve.
A final global view of the above described dynamics is given in figure 34, which shows the time-integrated circulation of the ‘core’ ventricular flow. In the symmetry
![]() $x$
–
$x$
–
![]() $z$
plane, we have (arbitrarily) isolated the square region
$z$
plane, we have (arbitrarily) isolated the square region
![]() $S$
(
$S$
(
![]() $-0.5\leqslant x\leqslant 0.5$
and
$-0.5\leqslant x\leqslant 0.5$
and
![]() $1.0\leqslant z\leqslant 2.0$
), far enough from the boundaries, and integrated the out-of-plane vorticity component
$1.0\leqslant z\leqslant 2.0$
), far enough from the boundaries, and integrated the out-of-plane vorticity component
![]() $\unicode[STIX]{x1D714}_{y}$
to obtain a circulation
$\unicode[STIX]{x1D714}_{y}$
to obtain a circulation
![]() $\unicode[STIX]{x1D6E4}_{y}(t)=\int _{S}\unicode[STIX]{x1D714}_{y}\,\text{d}S$
. This quantity has been time-averaged over the cycle through
$\unicode[STIX]{x1D6E4}_{y}(t)=\int _{S}\unicode[STIX]{x1D714}_{y}\,\text{d}S$
. This quantity has been time-averaged over the cycle through
![]() $\unicode[STIX]{x1D6FA}(t)=(\int _{0}^{t}\unicode[STIX]{x1D6E4}_{y}(\unicode[STIX]{x1D70F})\,\text{d}\unicode[STIX]{x1D70F})/t$
, and the result is reported for the three mitral valves at
$\unicode[STIX]{x1D6FA}(t)=(\int _{0}^{t}\unicode[STIX]{x1D6E4}_{y}(\unicode[STIX]{x1D70F})\,\text{d}\unicode[STIX]{x1D70F})/t$
, and the result is reported for the three mitral valves at
![]() $EF=40\,\%$
in figure 34. The strongest mean flow rotation is produced by the natural valve, while the biological prosthesis, even if it misses the initial peak, has a comparable recirculation strength at the end of the cycle. Again, the mechanical valve is the one inducing the weakest large-scale rotation of the core flow because of the flow transition to small scales that cross-diffuse into one another and prevent the formation of a strong coherent vortex.
$EF=40\,\%$
in figure 34. The strongest mean flow rotation is produced by the natural valve, while the biological prosthesis, even if it misses the initial peak, has a comparable recirculation strength at the end of the cycle. Again, the mechanical valve is the one inducing the weakest large-scale rotation of the core flow because of the flow transition to small scales that cross-diffuse into one another and prevent the formation of a strong coherent vortex.
Before concluding this discussion, we wish to comment on how the present findings relate to the clinical literature, according to which the free event survival curves of mitral valve replacement in a five-year follow-up (but also 10 or 15 years) are very similar for mechanical bileaflet and bioprosthetic valves despite the superior haemodynamics of the latter claimed in this study. In the paper by Chikwe et al. (Reference Chikwe, Yuting, Chiang, Egorova, Itagaki and Adams2015), a cohort of 3433 patients, all in the age range 50–69 and with mitral disease requiring valve replacement, showed that indeed ‘no survival difference was observed between use of mechanical prosthetic and bioprosthetic mitral valves’. However, the breakdown of the data evidenced that the causes of deaths were very different for the two classes of prostheses with ‘the incidences of stroke and bleeding events … significantly higher in those who received mechanical prosthetic mitral valves’ and ‘the incidence of reoperation … lower in the mechanical prosthesis group’ (Chikwe et al. Reference Chikwe, Yuting, Chiang, Egorova, Itagaki and Adams2015). More quantitatively, for the bileaflet implantations, strokes accounted for 15 % of lethal events, while for bioprosthetic valves they were only 6.8 %, thus evidencing a higher propensity of the mechanical valves to thromboembolism. The other relevant difference is in the bleedings, which were 14.9 % for mechanical valves and 9 % for the biological ones; the increased bleeding is a consequence of the lifelong anticoagulant therapy that the recipients of mechanical valves have to take to prevent clot formation. On the other hand, bioprosthetic valves degenerate more rapidly, especially in non-elderly patients, and the deaths caused by reoperation amounted to 5 % for the mechanical and 11 % for the bioprosthetic valves. It appears that these numbers miraculously balance, so that the overall fatality rates are roughly the same (Chikwe et al. Reference Chikwe, Yuting, Chiang, Egorova, Itagaki and Adams2015).
Analogous figures come from Hammermeister et al. (Reference Hammermeister, Sethi, Henderson, Grover, Oprian and Rahimtoola2000), who analysed two groups of 88 and 93 patients who had the mitral valve replaced with a mechanical or a biological prosthesis respectively. The follow-up at 15 years showed that the fatality rate from any cause was almost the same (81 % versus 79 %), although the single causes were different, with 53 % of bleeding events for the mechanical valve and 31 % for the bioprosthesis, but 25 % versus 50 % for reoperation and 5 % versus 40 % for primary valve failure.
Unfortunately, the analyses of Hammermeister et al. (Reference Hammermeister, Sethi, Henderson, Grover, Oprian and Rahimtoola2000) and Chikwe et al. (Reference Chikwe, Yuting, Chiang, Egorova, Itagaki and Adams2015) do not distinguish the patients with different ejection fractions, while Qiu et al. (Reference Qiu, Chen, Xu, Jiang, Xiao, Liu and Wang2010), who considered mechanical and biological mitral valve replacements in dysfunctional ventricles, did not separate the deaths that occurred with different valve models. Nevertheless, the statistics reported in Cen et al. (Reference Cen, Glower, Landolfo, Lowe, Davis, Wolfe, Pieper and Peterson2001) confirm that for physiological ejection fractions (in the range of 50 %), both the mechanical and the prosthetic valves perform adequately, while De Bacco et al. (Reference De Bacco, Sartori, Sant’Anna, Santos, Prates, Kalil and Nesralla2009) reported that in mechanical mitral valve replacement, a low-ejection-fraction ventricle is one of the most negative prognostic factors. Both results are consistent with our findings.
As a relevant point, we note that the acceptable performance of the mechanical valves comes at the cost of a heavy anticoagulant therapy which has to be carefully tuned in order to prevent clot formation but, at the same time, to avoid haemorrhagic events. In developed countries, even under close surveillance, it induces a 2 % fatality event rate per year (Cannegieter, Rosendaal & Briet Reference Cannegieter, Rosendaal and Briet1994; Cannegieter et al. Reference Cannegieter, Rosendaal, Wintzen, van der Meer, Vandenbroucke and Briët1995). At present, this therapy aims at maintaining the INR (‘international normalized ratio’, an indicator of the blood coagulation time) above a given threshold, whose value depends on the presence of a mechanical valve prosthesis, but it does not change for different ejection fractions of the left ventricle. It might be possible that if the anticoagulant dose were tailored also to the ventricle efficiency, some of its negative side effects could be mitigated.
5 Closing remarks
In this paper, the flow in the left ventricle with different types of mitral valves has been analysed, for different pumping efficiencies of the system. The reference case of a natural valve has evidenced the highly synergistic nature of the flow, with an interplay between the ventricle and valve dynamics that prevents the formation of stagnant flow regions, considered as a negative predictive factor for infarction and stroke.
The results have shown that for a healthy ventricle with an ejection fraction
![]() $EF=60\,\%$
, both the biological and the mechanical prostheses perform adequately, even if the former has better haemodynamics than the latter. Both of them produce a mitral jet that is strong enough to penetrate up to the apex of the ventricle and generate a beneficial large-scale recirculation that ‘washes’ the inner ventricular wall (endocardium). In contrast, in a ventricle with a reduced efficiency (
$EF=60\,\%$
, both the biological and the mechanical prostheses perform adequately, even if the former has better haemodynamics than the latter. Both of them produce a mitral jet that is strong enough to penetrate up to the apex of the ventricle and generate a beneficial large-scale recirculation that ‘washes’ the inner ventricular wall (endocardium). In contrast, in a ventricle with a reduced efficiency (
![]() $EF=40\,\%$
), which is a possible condition when a valve replacement is required, the mitral jet has a reduced momentum and the perturbations induced by the prostheses can decrease the penetration of the jet below the required level. This is the case for the mechanical bileaflet valve, which produces the highest transvalvular pressure drop and causes a transition of the coherent mitral jet to incoherent small scales; this prevents the jet from reaching the ventricle apex and causes blood stagnation (Badas, Domenichini & Querzoli Reference Badas, Domenichini and Querzoli2016).
$EF=40\,\%$
), which is a possible condition when a valve replacement is required, the mitral jet has a reduced momentum and the perturbations induced by the prostheses can decrease the penetration of the jet below the required level. This is the case for the mechanical bileaflet valve, which produces the highest transvalvular pressure drop and causes a transition of the coherent mitral jet to incoherent small scales; this prevents the jet from reaching the ventricle apex and causes blood stagnation (Badas, Domenichini & Querzoli Reference Badas, Domenichini and Querzoli2016).
This observation could be a novel factor to be taken into account when deciding whether a biological or a mechanical prosthetic valve should be used for a mitral valve replacement. At present, the best practice gives the highest weight to the balance between life expectation and prosthesis durability: since a biological valve is expected to perform for 15–20 years, patients with a longer life expectation receive a mechanical valve. The results of the present investigation suggest that among the decision factors, the efficiency of the ventricle should also be considered, since a mechanical valve implanted in a ventricle with an ejection fraction of 40 % or below might lead to flow stasis and the formation of dangerous clots.
These findings are fully consistent with the clinical literature, which, even if it reports nearly identical fatality rates for the follow-up of mitral replacement with mechanical valves or bioprostheses (Hammermeister et al. Reference Hammermeister, Sethi, Henderson, Grover, Oprian and Rahimtoola2000; Chikwe et al. Reference Chikwe, Yuting, Chiang, Egorova, Itagaki and Adams2015), indicates that the causes of death are very different. In addition, Cen et al. (Reference Cen, Glower, Landolfo, Lowe, Davis, Wolfe, Pieper and Peterson2001) confirm that for ejection fractions in the range of 50 %, both the mechanical and the prosthetic valves perform adequately, while De Bacco et al. (Reference De Bacco, Sartori, Sant’Anna, Santos, Prates, Kalil and Nesralla2009) state that an impaired ventricle is among the most negative prognostic factors for a mitral valve replacement with a mechanical prosthesis.
Before concluding this paper, we wish to make a few comments about the similarities and differences between our computational model and real ventricular flow. As mentioned in § 2.1, the development of the numerical model was initially guided by a companion experiment, of which the former is a digital replica. The final result is a quite complex numerical tool that can cope with a full FSI with rigid and deformable bodies within realistic geometries and flow parameters. Despite the considerable computational effort, there are still relevant differences between the present model and the intended real problem which should be taken into account when applying the results to clinical cases. For example, the model has a fixed mitral plane and a movable apex, while real left ventricles have a movable mitral plane and (nearly) fixed apex. Since the (base–apex) pressure gradient is proportional to the time derivative of the velocity, this might introduce differences between the present model and the real flow. However, if, by a linear extrapolation, we assume that the apex displacement is twice that of the centroid, from figure 7(c,d), we can estimate a maximum non-dimensional apex acceleration of
![]() $a_{A}\approx 8$
(a displacement of 0.54 unit lengths in
$a_{A}\approx 8$
(a displacement of 0.54 unit lengths in
![]() $1/4$
of the cycle period). On the other hand, from figure 12, using a sine to approximate the inflow curve during the first
$1/4$
of the cycle period). On the other hand, from figure 12, using a sine to approximate the inflow curve during the first
![]() $1/3$
of the cycle, a non-dimensional acceleration can be computed for the fluid at the inflow of
$1/3$
of the cycle, a non-dimensional acceleration can be computed for the fluid at the inflow of
![]() $a_{F}=U_{peak}2\unicode[STIX]{x03C0}/(0.3T)\approx 25$
. The fluid acceleration at the ventricle base must be 4–5 times larger, since the flow further accelerates through the mitral valve and the peak velocities in the ventricle are 4–5 times larger than at the inflow (see figure 14). According to these estimates, the apex acceleration is at least one order of magnitude smaller than the accelerations induced in the fluid by the imposed inflow/outflow; we expect the effect of the former to be negligible.
$a_{F}=U_{peak}2\unicode[STIX]{x03C0}/(0.3T)\approx 25$
. The fluid acceleration at the ventricle base must be 4–5 times larger, since the flow further accelerates through the mitral valve and the peak velocities in the ventricle are 4–5 times larger than at the inflow (see figure 14). According to these estimates, the apex acceleration is at least one order of magnitude smaller than the accelerations induced in the fluid by the imposed inflow/outflow; we expect the effect of the former to be negligible.
Another difference is that in our model the mitral annulus is planar and rigid, while in the real heart the shape changes during the heartbeat and assumes a saddle shape. According to Levine et al. (Reference Levine, Triulzi, Harrigan and Weyman1987), Salgo et al. (Reference Salgo, Gorman, Gorman, Jackson, Bowen, Plappert, Sutton and Edmundus2002), Votta et al. (Reference Votta, Caiani, Veronesi, Soncini, Montevecchi and Redaelli2008) and Mahmood et al. (Reference Mahmood, Gorman, Subramanian, Gorman, Panzica, Hagberg, Lerner, Hess, Maslow and Khabbaz2010), the mitral annulus is flat during diastole and becomes saddle shaped only during systole. In particular, Salgo et al. (Reference Salgo, Gorman, Gorman, Jackson, Bowen, Plappert, Sutton and Edmundus2002) and Votta et al. (Reference Votta, Caiani, Veronesi, Soncini, Montevecchi and Redaelli2008) found that the annulus non-planarity mainly affects the mobility of the posterior leaflet and facilitates the valve closure. In this paper, however, we are mainly concerned with the diastolic phase when the mitral valve opens and the ventricular flow is generated. Therefore, we expect this feature not to significantly affect our conclusions. A similar argument can be used to assess the effects of the different dimensions of the anterior and posterior leaflets of a natural mitral valve: in our model the vertical lengths of the leaflets are comparable, while in the real heart the posterior is approximately
![]() $1/3$
shorter.
$1/3$
shorter.
Another relevant difference is the ventricle dynamics, which, even if fully coupled with the flow, is passive and driven by the prescribed inflow/outflow (figure 12). This is different from the real heart, in which the ventricle actively contracts during the systole and determines the outflow rather than adapting to it. In addition, the contraction is caused by an electrical signal that propagates through the interventricular septum, reaches the apex and moves up to the ventricle following a helical path (Kocica et al. Reference Kocica, Corno, Carreras-Costa, Ballester-Rodes, Moghbel, Cueva, Lackovic, Kanjuh and Torrent-Guasp2006). Therefore, the ventricle contraction is not homogeneous but instead starts from the apex and produces a twist of the myocardium; this implies that the flow during the systole could be different from that observed in the present paper. Nevertheless, in the diastolic phase, the myocardium relaxes and it adapts to the inflow produced by the pressure of the blood coming from the pulmonary veins and the atrial contraction. The diastolic flow is therefore closer to the flow investigated here. Moreover, the inner structure of the endocardium, which is characterized by irregular grooves (trabeculae), is far from the smooth surface modelled here. As shown by Vedula et al. (Reference Vedula, Seo, Lardo and Mittal2016), the flow within the trabeculae is closely linked to the active contraction of the myocardium, but this feature mainly affects the near-wall region and much less the large-scale features that we have analysed here. A final difference is the presence, in the natural valve, of the cordae tendinae, flexible and inextensible ‘filaments’ that link the leaflet tips to the myocardium through the papillary muscles; these structures tense during the systole and prevent the leaflets from everting into the atrium. In the present simulations, only their kinematic effects on the leaflet dynamics of the natural valve have been considered, while their interaction with the ventricular flow was absent. It is worth mentioning, however, that when a prosthesis is implanted, the cordae tendinae are removed from the ventricle to avoid any interference with the valve (while the papillary muscles are preserved for the integrity of the myocardium). Consequently, the present flows with mechanical and biological valves are similar to real ones.
According to the above discussion, there are two main ongoing investigations that are aimed at making the numerical model closer to real heart flow. The first is the addition of the cordae tendinae to the geometrical configuration and the second is the addition of an electrophysiological model (Clayton et al. Reference Clayton, Bernus, Cherry, Dierckx, Fenton, Mirabella, Panfilov, Sachse, Seemann and Zhang2011) that accounts for the anisotropic propagation of the electrical signal through the myocardium and allows for its active contraction. These will both be the topics of forthcoming papers.
Acknowledgements
The authors wish to thank V. Spandan, F. Viola and R. Mittal for suggestions on the manuscript and discussions on the results. The invaluable help of D. De Manna, F. Sposato and S. Santamaria with the laboratory experiments is also gratefully acknowledged. This work has been partially funded by the Italian Ministry of University and Scientific Research (MIUR), PRIN2012, grant no. 2012HMR7CF.







































