1 Introduction: from turbulence to coherent structures and dynamical systems
Turbulence, paraphrasing Luis Buñuel that obscure object of desire, controls flows and fluxes or more precisely flows through fluxes. Through a complex cascade of motions at all scales, it mixes momentum and passive or active scalars, and dissipates, by breaking down to the thermal agitation, the energy that was once at large scale. Reynolds (Reference Reynolds1883) was the first to observe the capacity of turbulence to mix momentum. He also observed that turbulence possesses shape with puffs made of vortices and with frontiers between order and disorder. Nearly a century later the work of Brown & Roshko (Reference Brown and Roshko1974) and Winant & Browand (Reference Winant and Browand1974) brought back turbulence from the spectral space to real space re-introducing the idea of coherent structures. After the successes of Kolmogorov’s (Reference Kolmogorov1941) statistical theory, where the concept of inertial energy cascade imposes the scaling laws of the two-point velocity correlation, these studies reinstated the role of phase coherence associated with the, local in space, conservation of the vorticity flux. A few years later the cryogenic convection experiment in liquid helium by Maurer & Libchaber (Reference Maurer and Libchaber1979), where period doubling bifurcation announces the onset of turbulence, demonstrated that the phase between frequencies also matters. Together the coherent structures and the dynamical system constitute a single entity coherent in space and time, an attractor, shaping turbulent flows.
The work by Lefauve et al. (Reference Lefauve, Partridge, Zhou, Dalziel, Caulfield and Linden2018) is claiming back the heritage of the seventies, revisiting the road to the strange attractor by demonstrating experimentally the existence of a coherent structure in a stratified shear flow and its remarkable link to the leading linear eigenmode corresponding to a Holmboe wave.
2 Overview
Shear is the source for instability, mixing and turbulence since any displacement along the shear will transport momentum in a differential manner, creating perturbations. This mechanism leads to the celebrated Kelvin–Helmholtz instability rolling the shear into spanwise vortices, and also to streamwise striation via the lift-up mechanism where weak streamwise vortices produce alternate low and high-speed streaks (Schmid & Henningson Reference Schmid and Henningson2001). When the fluid is stably stratified, the buoyancy forces counteract vertical motion, and generate waves characterised by the buoyancy frequency
 $N$
. The ratio of
$N$
. The ratio of
 $N$
to the shear rate gives the gradient Richardson number
$N$
to the shear rate gives the gradient Richardson number
 $Ri$
and determines the stability. In uniform stratification Kelvin–Helmholtz instability will only occur when
$Ri$
and determines the stability. In uniform stratification Kelvin–Helmholtz instability will only occur when
 $Ri<1/4$
. When the variation of density is sharp another instability described by Holmboe (Reference Holmboe1962) takes over when the Kelvin–Helmholtz mechanism is stabilised. Even when the density interface is centred on shear, the Holmboe instability breaks the horizontal symmetry and becomes propagative. The physics of the Holmboe mode is easy to understand in the limit of strong stratification when it corresponds to a gravity wave at the density interface coupled with a Rossby-like wave inside the shear layer. Instability occurs when these two waves are spatially and temporally locked.
$Ri<1/4$
. When the variation of density is sharp another instability described by Holmboe (Reference Holmboe1962) takes over when the Kelvin–Helmholtz mechanism is stabilised. Even when the density interface is centred on shear, the Holmboe instability breaks the horizontal symmetry and becomes propagative. The physics of the Holmboe mode is easy to understand in the limit of strong stratification when it corresponds to a gravity wave at the density interface coupled with a Rossby-like wave inside the shear layer. Instability occurs when these two waves are spatially and temporally locked.
The Lefauve et al. (Reference Lefauve, Partridge, Zhou, Dalziel, Caulfield and Linden2018) experiment is an extremely clever new set-up that allows the exploration of a large variety of exchange flows in a controlled manner by using a closed tube tilted with an angle
 $\unicode[STIX]{x1D703}$
from the horizontal between two tanks (see the title figure). The flow is hydraulically controlled and the velocity magnitude
$\unicode[STIX]{x1D703}$
from the horizontal between two tanks (see the title figure). The flow is hydraulically controlled and the velocity magnitude
 $U=\sqrt{g^{\prime }H}$
is only a function of the height of the tube
$U=\sqrt{g^{\prime }H}$
is only a function of the height of the tube
 $H$
and the reduced gravity
$H$
and the reduced gravity
 $g^{\prime }=\unicode[STIX]{x0394}\unicode[STIX]{x1D70C}g/\unicode[STIX]{x1D70C}_{0}$
(
$g^{\prime }=\unicode[STIX]{x0394}\unicode[STIX]{x1D70C}g/\unicode[STIX]{x1D70C}_{0}$
(
 $g$
the gravity,
$g$
the gravity,
 $\unicode[STIX]{x1D70C}_{0}$
the mean density,
$\unicode[STIX]{x1D70C}_{0}$
the mean density,
 $\unicode[STIX]{x0394}\unicode[STIX]{x1D70C}$
the density difference), independent of the tilt angle
$\unicode[STIX]{x0394}\unicode[STIX]{x1D70C}$
the density difference), independent of the tilt angle
 $\unicode[STIX]{x1D703}>0$
, and the Reynolds number of the flow,
$\unicode[STIX]{x1D703}>0$
, and the Reynolds number of the flow,
 $Re=H\sqrt{g^{\prime }H}/4\unicode[STIX]{x1D708}$
, is also independent of
$Re=H\sqrt{g^{\prime }H}/4\unicode[STIX]{x1D708}$
, is also independent of
 $\unicode[STIX]{x1D703}$
. The shear is driven by the component of the gravity along the tube,
$\unicode[STIX]{x1D703}$
. The shear is driven by the component of the gravity along the tube,
 $g^{\prime }\sin \unicode[STIX]{x1D703}$
, and its work,
$g^{\prime }\sin \unicode[STIX]{x1D703}$
, and its work,
 $\unicode[STIX]{x1D716}_{0}\sim Ug^{\prime }\sin \unicode[STIX]{x1D703}$
, represents the rate of injection of energy. Since the flow is stationary and considered homogeneous far from the inlets,
$\unicode[STIX]{x1D716}_{0}\sim Ug^{\prime }\sin \unicode[STIX]{x1D703}$
, represents the rate of injection of energy. Since the flow is stationary and considered homogeneous far from the inlets,
 $\unicode[STIX]{x1D716}_{0}$
is also the rate of dissipation of total kinetic energy. The second parameter is then the buoyancy Reynolds number
$\unicode[STIX]{x1D716}_{0}$
is also the rate of dissipation of total kinetic energy. The second parameter is then the buoyancy Reynolds number
 $Re_{b}$
that measures the ratio between the largest scale not affected by the stratification (known as the Ozmidov scale) to the smallest scale not affected by dissipation (known as the Kolmogorov scale). Since both the Ozmidov and Kolmogorov scales depend on
$Re_{b}$
that measures the ratio between the largest scale not affected by the stratification (known as the Ozmidov scale) to the smallest scale not affected by dissipation (known as the Kolmogorov scale). Since both the Ozmidov and Kolmogorov scales depend on
 $\unicode[STIX]{x1D716}_{0}$
, the buoyancy Reynolds number
$\unicode[STIX]{x1D716}_{0}$
, the buoyancy Reynolds number
 $Re_{b}$
is a function of
$Re_{b}$
is a function of
 $\sin \unicode[STIX]{x1D703}$
and its estimate gives
$\sin \unicode[STIX]{x1D703}$
and its estimate gives
 $Re_{b}=Re\sin \unicode[STIX]{x1D703}$
. The ability to reach large
$Re_{b}=Re\sin \unicode[STIX]{x1D703}$
. The ability to reach large
 $Re_{b}$
is one of the great merits of the Lefauve et al. (Reference Lefauve, Partridge, Zhou, Dalziel, Caulfield and Linden2018) experiment, since only large
$Re_{b}$
is one of the great merits of the Lefauve et al. (Reference Lefauve, Partridge, Zhou, Dalziel, Caulfield and Linden2018) experiment, since only large
 $Re_{b}$
are pertinent for geophysical applications and it has been a long-lasting challenge to be able to realise experiments in this regime.
$Re_{b}$
are pertinent for geophysical applications and it has been a long-lasting challenge to be able to realise experiments in this regime.
Figure 1. Troubling resemblance between spanwise vorticity contour of (a) the structure appearing in the experiment and (b) the Holmboe mode from stability analysis.
The second particular achievement of the work is the fully resolved three-dimensional (3-D) particle image velocimetry, coupled with a laser induced fluorescence technique; together, these impressive measurement devices give the three-component velocity and density fields simultaneously over a three-dimensional volume as a function of time. The isosurface of the phase averaged spanwise vorticity (figure 1
a) represents the coherent structure observed in the experiment that evokes the familiar shape of the Loch Ness monster (S. Dalziel, personal communication). The regularity of the flow allows the phase averaging of the fields revealing fine details of the coherent beast that has emerged from the loch of measurement noise.
The isosurface of the spanwise vorticity obtained by superposing the locally parallel base flow with the leading mode given by the linear stability analysis of the associated 2-D eigenvalue problem is shown in figure 1(b). The base flow has been deduced using an average conditioned on the location of the interface, i.e. with the vertical coordinate translated at each time to be centred on the largest density gradient. The amplitude of the perturbation, not imposed by the linear theory, is determined by matching the perturbation vorticity, measured in the experiment.
The resemblance of the coherent structure observed experimentally and the leading eigenmode is astonishing: even the small details at the foot of the beast seem to correspond. This success of modern stability theory of parallel flows with two inhomogeneous directions reveals that the structure has emerged from the bifurcation of the base flow following the classical supercritical route to disorder.
3 The future will be real, four-dimensional, unsteady, inhomogeneous and nonlinear
The experimental technique reported by Lefauve et al. (Reference Lefauve, Partridge, Zhou, Dalziel, Caulfield and Linden2018) is among the first to resolve in time and space the three components of the velocity field with great precision. We may now face the complexity of real flows: non-parallel, non-stationary and observe the bifurcations, the nonlinear attractors and, beyond, the pattern-formation dynamics in both space and time. All the classical experiments should be reconsidered and will reveal new physics involving 3-D or even 4-D motions.
Modern stability theory, as demonstrated masterfully in Lefauve et al. (Reference Lefauve, Partridge, Zhou, Dalziel, Caulfield and Linden2018), is now able to solve for 2-D eigenvalue problems. The straightforward extension would be to solve for the impulse response or for the signalling problem to analyse the convective or absolute nature of the confined Holmboe instability. From the phase velocity
 $c$
as a function of the wavenumber
$c$
as a function of the wavenumber
 $k$
reported on figure 6(b), it seems that although the phase speed is negative its group velocity given by
$k$
reported on figure 6(b), it seems that although the phase speed is negative its group velocity given by
 $v_{G}=c+k\,\text{d}c/\text{d}k$
is positive but extremely small, meaning that this mode may be absolutely unstable. For the 2-D broken line profile, Ortiz, Chomaz & Loiseleux (Reference Ortiz, Chomaz and Loiseleux2002) have shown that the Holmboe modes are absolutely unstable for different ranges of the velocity at the interface. It remains to be seen whether this is the case for the experimental shear and density profiles.
$v_{G}=c+k\,\text{d}c/\text{d}k$
is positive but extremely small, meaning that this mode may be absolutely unstable. For the 2-D broken line profile, Ortiz, Chomaz & Loiseleux (Reference Ortiz, Chomaz and Loiseleux2002) have shown that the Holmboe modes are absolutely unstable for different ranges of the velocity at the interface. It remains to be seen whether this is the case for the experimental shear and density profiles.
Extension to 3-D problems, not assuming parallel flow, is also at hand and, associated with the adjoint 3-D problem, it should be possible to quantify the inlet effect, the sensitivity to base flow modification and both the self-sustained modes of the spectrum and the noise forced modes from the pseudospectrum (Schmid & Henningson Reference Schmid and Henningson2001).
Of course, as proposed be Lefauve et al. (Reference Lefauve, Partridge, Zhou, Dalziel, Caulfield and Linden2018), the linear analysis may be extended to consider the weakly nonlinear dynamics, again using adjoint modes and the receptivity to base flow modification and harmonics generation. Such a nonlinear stability analysis may take into account the coupling through the base flow of the left and right moving Holmboe modes, and cast their interactions into a two-amplitude normal form that may describe secondary bifurcations to chaos. Such a nonlinear analysis, with one or two modes, will predict the nonlinear base flow modification induced by the development of Holmboe instability. Considering the shape shown in figure 1, one of the main effects will be the creation of a mixed zone close to the head of the mode in the middle of the tube that should be induced by a recirculation pumping fluid above and below the interface.
But the most interesting and expected extension of the work, both experimentally and theoretically, would be the application to real submarine canyons where the confinement effect should be similar to the strong effect observed here. The nonlinear recirculation mentioned above, should also be present, leading to sharpening the interface and generating more mixing.
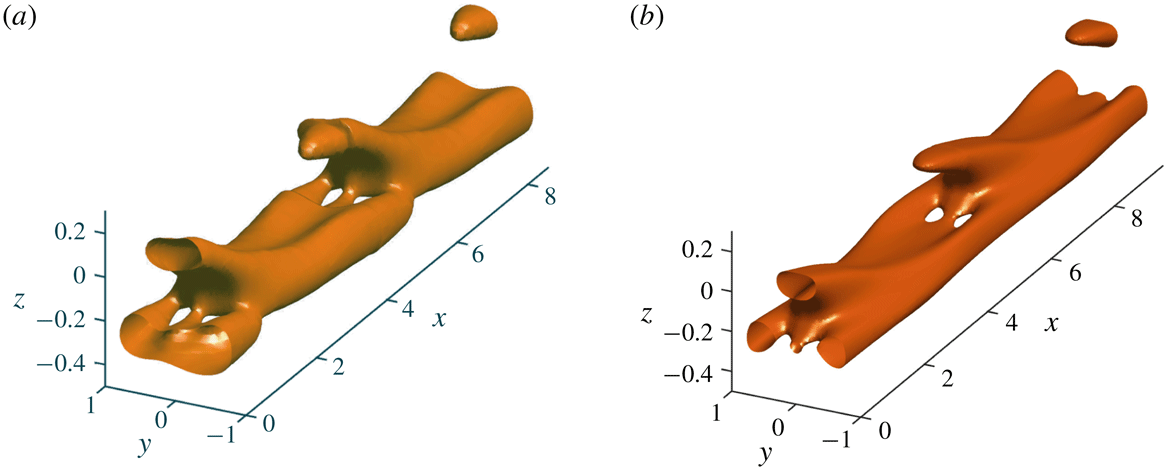




1 Introduction: from turbulence to coherent structures and dynamical systems
Turbulence, paraphrasing Luis Buñuel that obscure object of desire, controls flows and fluxes or more precisely flows through fluxes. Through a complex cascade of motions at all scales, it mixes momentum and passive or active scalars, and dissipates, by breaking down to the thermal agitation, the energy that was once at large scale. Reynolds (Reference Reynolds1883) was the first to observe the capacity of turbulence to mix momentum. He also observed that turbulence possesses shape with puffs made of vortices and with frontiers between order and disorder. Nearly a century later the work of Brown & Roshko (Reference Brown and Roshko1974) and Winant & Browand (Reference Winant and Browand1974) brought back turbulence from the spectral space to real space re-introducing the idea of coherent structures. After the successes of Kolmogorov’s (Reference Kolmogorov1941) statistical theory, where the concept of inertial energy cascade imposes the scaling laws of the two-point velocity correlation, these studies reinstated the role of phase coherence associated with the, local in space, conservation of the vorticity flux. A few years later the cryogenic convection experiment in liquid helium by Maurer & Libchaber (Reference Maurer and Libchaber1979), where period doubling bifurcation announces the onset of turbulence, demonstrated that the phase between frequencies also matters. Together the coherent structures and the dynamical system constitute a single entity coherent in space and time, an attractor, shaping turbulent flows.
The work by Lefauve et al. (Reference Lefauve, Partridge, Zhou, Dalziel, Caulfield and Linden2018) is claiming back the heritage of the seventies, revisiting the road to the strange attractor by demonstrating experimentally the existence of a coherent structure in a stratified shear flow and its remarkable link to the leading linear eigenmode corresponding to a Holmboe wave.
2 Overview
Shear is the source for instability, mixing and turbulence since any displacement along the shear will transport momentum in a differential manner, creating perturbations. This mechanism leads to the celebrated Kelvin–Helmholtz instability rolling the shear into spanwise vortices, and also to streamwise striation via the lift-up mechanism where weak streamwise vortices produce alternate low and high-speed streaks (Schmid & Henningson Reference Schmid and Henningson2001). When the fluid is stably stratified, the buoyancy forces counteract vertical motion, and generate waves characterised by the buoyancy frequency $N$
. The ratio of
$N$
. The ratio of
 $N$
to the shear rate gives the gradient Richardson number
$N$
to the shear rate gives the gradient Richardson number
 $Ri$
and determines the stability. In uniform stratification Kelvin–Helmholtz instability will only occur when
$Ri$
and determines the stability. In uniform stratification Kelvin–Helmholtz instability will only occur when
 $Ri<1/4$
. When the variation of density is sharp another instability described by Holmboe (Reference Holmboe1962) takes over when the Kelvin–Helmholtz mechanism is stabilised. Even when the density interface is centred on shear, the Holmboe instability breaks the horizontal symmetry and becomes propagative. The physics of the Holmboe mode is easy to understand in the limit of strong stratification when it corresponds to a gravity wave at the density interface coupled with a Rossby-like wave inside the shear layer. Instability occurs when these two waves are spatially and temporally locked.
$Ri<1/4$
. When the variation of density is sharp another instability described by Holmboe (Reference Holmboe1962) takes over when the Kelvin–Helmholtz mechanism is stabilised. Even when the density interface is centred on shear, the Holmboe instability breaks the horizontal symmetry and becomes propagative. The physics of the Holmboe mode is easy to understand in the limit of strong stratification when it corresponds to a gravity wave at the density interface coupled with a Rossby-like wave inside the shear layer. Instability occurs when these two waves are spatially and temporally locked.
The Lefauve et al. (Reference Lefauve, Partridge, Zhou, Dalziel, Caulfield and Linden2018) experiment is an extremely clever new set-up that allows the exploration of a large variety of exchange flows in a controlled manner by using a closed tube tilted with an angle $\unicode[STIX]{x1D703}$
from the horizontal between two tanks (see the title figure). The flow is hydraulically controlled and the velocity magnitude
$\unicode[STIX]{x1D703}$
from the horizontal between two tanks (see the title figure). The flow is hydraulically controlled and the velocity magnitude
 $U=\sqrt{g^{\prime }H}$
is only a function of the height of the tube
$U=\sqrt{g^{\prime }H}$
is only a function of the height of the tube
 $H$
and the reduced gravity
$H$
and the reduced gravity
 $g^{\prime }=\unicode[STIX]{x0394}\unicode[STIX]{x1D70C}g/\unicode[STIX]{x1D70C}_{0}$
(
$g^{\prime }=\unicode[STIX]{x0394}\unicode[STIX]{x1D70C}g/\unicode[STIX]{x1D70C}_{0}$
(
 $g$
the gravity,
$g$
the gravity,
 $\unicode[STIX]{x1D70C}_{0}$
the mean density,
$\unicode[STIX]{x1D70C}_{0}$
the mean density,
 $\unicode[STIX]{x0394}\unicode[STIX]{x1D70C}$
the density difference), independent of the tilt angle
$\unicode[STIX]{x0394}\unicode[STIX]{x1D70C}$
the density difference), independent of the tilt angle
 $\unicode[STIX]{x1D703}>0$
, and the Reynolds number of the flow,
$\unicode[STIX]{x1D703}>0$
, and the Reynolds number of the flow,
 $Re=H\sqrt{g^{\prime }H}/4\unicode[STIX]{x1D708}$
, is also independent of
$Re=H\sqrt{g^{\prime }H}/4\unicode[STIX]{x1D708}$
, is also independent of
 $\unicode[STIX]{x1D703}$
. The shear is driven by the component of the gravity along the tube,
$\unicode[STIX]{x1D703}$
. The shear is driven by the component of the gravity along the tube,
 $g^{\prime }\sin \unicode[STIX]{x1D703}$
, and its work,
$g^{\prime }\sin \unicode[STIX]{x1D703}$
, and its work,
 $\unicode[STIX]{x1D716}_{0}\sim Ug^{\prime }\sin \unicode[STIX]{x1D703}$
, represents the rate of injection of energy. Since the flow is stationary and considered homogeneous far from the inlets,
$\unicode[STIX]{x1D716}_{0}\sim Ug^{\prime }\sin \unicode[STIX]{x1D703}$
, represents the rate of injection of energy. Since the flow is stationary and considered homogeneous far from the inlets,
 $\unicode[STIX]{x1D716}_{0}$
is also the rate of dissipation of total kinetic energy. The second parameter is then the buoyancy Reynolds number
$\unicode[STIX]{x1D716}_{0}$
is also the rate of dissipation of total kinetic energy. The second parameter is then the buoyancy Reynolds number
 $Re_{b}$
that measures the ratio between the largest scale not affected by the stratification (known as the Ozmidov scale) to the smallest scale not affected by dissipation (known as the Kolmogorov scale). Since both the Ozmidov and Kolmogorov scales depend on
$Re_{b}$
that measures the ratio between the largest scale not affected by the stratification (known as the Ozmidov scale) to the smallest scale not affected by dissipation (known as the Kolmogorov scale). Since both the Ozmidov and Kolmogorov scales depend on
 $\unicode[STIX]{x1D716}_{0}$
, the buoyancy Reynolds number
$\unicode[STIX]{x1D716}_{0}$
, the buoyancy Reynolds number
 $Re_{b}$
is a function of
$Re_{b}$
is a function of
 $\sin \unicode[STIX]{x1D703}$
and its estimate gives
$\sin \unicode[STIX]{x1D703}$
and its estimate gives
 $Re_{b}=Re\sin \unicode[STIX]{x1D703}$
. The ability to reach large
$Re_{b}=Re\sin \unicode[STIX]{x1D703}$
. The ability to reach large
 $Re_{b}$
is one of the great merits of the Lefauve et al. (Reference Lefauve, Partridge, Zhou, Dalziel, Caulfield and Linden2018) experiment, since only large
$Re_{b}$
is one of the great merits of the Lefauve et al. (Reference Lefauve, Partridge, Zhou, Dalziel, Caulfield and Linden2018) experiment, since only large
 $Re_{b}$
are pertinent for geophysical applications and it has been a long-lasting challenge to be able to realise experiments in this regime.
$Re_{b}$
are pertinent for geophysical applications and it has been a long-lasting challenge to be able to realise experiments in this regime.
Figure 1. Troubling resemblance between spanwise vorticity contour of (a) the structure appearing in the experiment and (b) the Holmboe mode from stability analysis.
The second particular achievement of the work is the fully resolved three-dimensional (3-D) particle image velocimetry, coupled with a laser induced fluorescence technique; together, these impressive measurement devices give the three-component velocity and density fields simultaneously over a three-dimensional volume as a function of time. The isosurface of the phase averaged spanwise vorticity (figure 1 a) represents the coherent structure observed in the experiment that evokes the familiar shape of the Loch Ness monster (S. Dalziel, personal communication). The regularity of the flow allows the phase averaging of the fields revealing fine details of the coherent beast that has emerged from the loch of measurement noise.
The isosurface of the spanwise vorticity obtained by superposing the locally parallel base flow with the leading mode given by the linear stability analysis of the associated 2-D eigenvalue problem is shown in figure 1(b). The base flow has been deduced using an average conditioned on the location of the interface, i.e. with the vertical coordinate translated at each time to be centred on the largest density gradient. The amplitude of the perturbation, not imposed by the linear theory, is determined by matching the perturbation vorticity, measured in the experiment.
The resemblance of the coherent structure observed experimentally and the leading eigenmode is astonishing: even the small details at the foot of the beast seem to correspond. This success of modern stability theory of parallel flows with two inhomogeneous directions reveals that the structure has emerged from the bifurcation of the base flow following the classical supercritical route to disorder.
3 The future will be real, four-dimensional, unsteady, inhomogeneous and nonlinear
The experimental technique reported by Lefauve et al. (Reference Lefauve, Partridge, Zhou, Dalziel, Caulfield and Linden2018) is among the first to resolve in time and space the three components of the velocity field with great precision. We may now face the complexity of real flows: non-parallel, non-stationary and observe the bifurcations, the nonlinear attractors and, beyond, the pattern-formation dynamics in both space and time. All the classical experiments should be reconsidered and will reveal new physics involving 3-D or even 4-D motions.
Modern stability theory, as demonstrated masterfully in Lefauve et al. (Reference Lefauve, Partridge, Zhou, Dalziel, Caulfield and Linden2018), is now able to solve for 2-D eigenvalue problems. The straightforward extension would be to solve for the impulse response or for the signalling problem to analyse the convective or absolute nature of the confined Holmboe instability. From the phase velocity $c$
as a function of the wavenumber
$c$
as a function of the wavenumber
 $k$
reported on figure 6(b), it seems that although the phase speed is negative its group velocity given by
$k$
reported on figure 6(b), it seems that although the phase speed is negative its group velocity given by
 $v_{G}=c+k\,\text{d}c/\text{d}k$
is positive but extremely small, meaning that this mode may be absolutely unstable. For the 2-D broken line profile, Ortiz, Chomaz & Loiseleux (Reference Ortiz, Chomaz and Loiseleux2002) have shown that the Holmboe modes are absolutely unstable for different ranges of the velocity at the interface. It remains to be seen whether this is the case for the experimental shear and density profiles.
$v_{G}=c+k\,\text{d}c/\text{d}k$
is positive but extremely small, meaning that this mode may be absolutely unstable. For the 2-D broken line profile, Ortiz, Chomaz & Loiseleux (Reference Ortiz, Chomaz and Loiseleux2002) have shown that the Holmboe modes are absolutely unstable for different ranges of the velocity at the interface. It remains to be seen whether this is the case for the experimental shear and density profiles.
Extension to 3-D problems, not assuming parallel flow, is also at hand and, associated with the adjoint 3-D problem, it should be possible to quantify the inlet effect, the sensitivity to base flow modification and both the self-sustained modes of the spectrum and the noise forced modes from the pseudospectrum (Schmid & Henningson Reference Schmid and Henningson2001).
Of course, as proposed be Lefauve et al. (Reference Lefauve, Partridge, Zhou, Dalziel, Caulfield and Linden2018), the linear analysis may be extended to consider the weakly nonlinear dynamics, again using adjoint modes and the receptivity to base flow modification and harmonics generation. Such a nonlinear stability analysis may take into account the coupling through the base flow of the left and right moving Holmboe modes, and cast their interactions into a two-amplitude normal form that may describe secondary bifurcations to chaos. Such a nonlinear analysis, with one or two modes, will predict the nonlinear base flow modification induced by the development of Holmboe instability. Considering the shape shown in figure 1, one of the main effects will be the creation of a mixed zone close to the head of the mode in the middle of the tube that should be induced by a recirculation pumping fluid above and below the interface.
But the most interesting and expected extension of the work, both experimentally and theoretically, would be the application to real submarine canyons where the confinement effect should be similar to the strong effect observed here. The nonlinear recirculation mentioned above, should also be present, leading to sharpening the interface and generating more mixing.