Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-18T05:58:53.511Z Has data issue: false hasContentIssue false
  • English
  • Français

Flat plate impact on water

Published online by Cambridge University Press:  12 July 2018

Hans C. Mayer  and
Rouslan Krechetnikov Open the ORCID record for Rouslan Krechetnikov [Opens in a new window]
Hans C. Mayer
Affiliation:
Department of Mechanical Engineering, University of California, Santa Barbara, CA 93106, USA
Rouslan Krechetnikov*
Affiliation:
Department of Mathematics, University of Alberta, Edmonton, AB T6G 2G1, Canada
*
†Email address for correspondence: krechet@ualberta.ca
Get access Rights & Permissions [Opens in a new window]

Abstract

While the classical problem of a flat plate impact on a water surface at zero dead-rise angle has been studied for a long time both theoretically and experimentally, it still presents a number of challenges and unsolved questions. Hitherto, the details of the flow field – especially at early times and close to the plate edge, where the classical inviscid theory predicts a singularity in the velocity field and thus in the free surface deflection, so-called ejecta – have not been studied experimentally, which led to mutually contradicting suppositions in the literature. On one hand, it motivated Yakimov’s self-similar scaling near the plate edge. On the other hand, a removal of the singularity was previously suggested with the help of the Kutta–Joukowsky condition at the plate edge, i.e. enforcing the free surface to depart tangentially to the plate. In the present experimental study we were able to overcome challenges with optical access and investigate, for moderate Reynolds (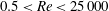$0.5<Re<25\,000$) and Weber (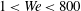$1<We<800$) numbers, both the flow fields and the free surface dynamics at the early stage of the water impact, when the penetration depth is small compared to the plate size, thus allowing us to compare to the classical water impact theory valid in the short time limit. This, in particular, enabled us to uncover the effects of viscosity and surface tension on the velocity field and ejecta evolution usually neglected in theoretical studies. While we were able to confirm the far-field inviscid and the near-edge Stokes theoretical scalings of the free surface profiles, Yakimov’s scaling of the velocity field proved to be inapplicable and the Kutta–Joukowsky condition not satisfied universally in the studied range of Reynolds and Weber numbers. Since the local near-edge phenomena cannot be considered independently of the complete water impact event, the experiments were also set up to study the entirety of the water impact phenomena under realistic conditions – presence of air phase and finite depth of penetration. This allowed us to obtain insights also into other key aspects of the water impact phenomena such as air entrapment and pocketing at the later stage when the impactor bottoms out. In our experiments the volume of trapped air proved not to decrease necessarily with the impact speed, an effect that has not been reported before. The observed fast initial retraction of the trapped air film along the plate bottom turned out to be a consequence of a negative pressure impulse generated upon the abrupt deceleration of the plate. This abrupt deceleration is also the cause of the subsequent air pocketing. Quantitative measurements are complemented with basic scaling models explaining the nature of both retraction of the trapped air and air pocket formation.

JFM classification

Interfacial Flows (free surface): Interfacial Flows (free surface)
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 850 , 10 September 2018 , pp. 1066 - 1116
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barenblatt, G. I. 1996 Scaling, Self-Similarity, and Intermediate Asymptotics: Dimensional Analysis and Intermediate Asymptotics. Cambridge University Press.Google Scholar
Bartolo, D., Josserand, C. & Bonn, D. 2005 Retraction dynamics of aqueous drops upon impact on non-wetting surfaces. J. Fluid Mech. 545, 329–338.Google Scholar
Batchelor, G. K. 1967 An Introduction to Fluid Dynamics. Cambridge University Press.Google Scholar
Bergmann, R., van der Meer, D., Gekle, S., van der Bos, A. & Lohse, D. 2009 Controlled impact of a disk on a water surface: cavity dynamics. J. Fluid Mech. 633, 381–409.Google Scholar
Chuang, S. L. 1966 Experiments on flat-bottom slamming. J. Ship Res. 10, 10–17.Google Scholar
Culick, F. E. C. 1960 Comments on a ruptured soap film. J. Appl. Phys. 31, 1128–1129.Google Scholar
Duez, C., Ybert, C., Clanet, C. & Bocquet, L. 2007 Making a splash with water repellency. Nat. Phys. 3, 180–183.Google Scholar
Ermanyuk, E. V. & Gavrilov, N. V. 2011 Experimental study of disk impact onto shallow water. J. Appl. Mech. Tech. Phys. 52, 889–895.Google Scholar
Ermanyuk, E. V. & Ohkusu, M. 2005 Impact of a disk on shallow water. J. Fluids Struct. 20, 345–357.Google Scholar
Galin, L. A. 1947 Impact of solid body on a compressible liquid surface. Prikl. Mat. Mekh. 11, 547–550.Google Scholar
Gekle, S., Peters, I. R., Gordillo, J. M., van der Meer, D. & Lohse, D. 2010 Supersonic air flow due to solid-liquid impact. Phys. Rev. Lett. 104, 024501.Google Scholar
Gekle, S., van der Bos, A., Bergmann, R., van der Meer, D. & Lohse, D. 2008 Noncontinuous Froude number scaling for the closure depth of a cylindrical cavity. Phys. Rev. Lett. 100, 084502.Google Scholar
Glasheen, J. W. & McMahon, T. A. 1996 Vertical water entry of disks at low Froude numbers. Phys. Fluids 8, 2078–2083.Google Scholar
Green, A. E. 1936 Note on the gliding of a plate on the surface of a stream. Math. Proc. Camb. Phil. Soc. 32, 248–252.Google Scholar
Greenhow, M. & Lin, W-M.1983 Nonlinear free surface effects: experiments and theory. Tech. Rep. 83–19. MIT.Google Scholar
Henderson, D. M., Segur, H. & Carter, J. D. 2010 Experimental evidence of stable wave patterns on deep water. J. Fluid Mech. 658, 247–278.Google Scholar
Hicks, P. D., Ermanyuk, E. V., Gavrilov, N. V. & Purvis, R. 2012 Air trapping at impact of a rigid sphere onto a liquid. J. Fluid Mech. 695, 310–320.Google Scholar
Huera-Huarte, F. J., Jeon, D. & Gharib, M. 2011 Experimental investigation of water slamming loads on panels. Ocean Engng 38, 1347–1355.Google Scholar
Hughes, O. F. 1972 Solution of the wedge entry problem by numerical conformal mapping. J. Fluid Mech. 56, 173–192.Google Scholar
Iafrati, A. & Korobkin, A. A. 2004 Initial stage of flat plate impact onto liquid free surface. Phys. Fluids 16, 2214–2227.Google Scholar
Iafrati, A. & Korobkin, A. A. 2008 Hydrodynamic loads during early stage of flat plate impact onto water surface. Phys. Fluids 20, 082104.Google Scholar
Iafrati, A. & Korobkin, A. A. 2011 Asymptotic estimates of hydrodynamic loads in the early stage of water entry of a circular disk. J. Engng Maths 69, 199–224.Google Scholar
Jalalisendi, M., Zhao, S. & Porfiri, M. 2017 Shallow water entry: modelling and experiments. J. Engng Maths 104, 131–156.Google Scholar
Jones, G. & Ray, W. A. 1941 The surface tension of solutions of electrolytes as a function of the concentration. III. Sodium Chloride. J. Am. Chem. Soc. 63, 3262–3263.Google Scholar
Jones, M. A. 2003 The separated flow of an inviscid fluid around a moving flat plate. J. Fluid Mech. 496, 405–441.Google Scholar
von Karman, T. H.1929 The impact on seaplane floats during landing. NACA Tech. Rep. 321.Google Scholar
Keller, J. B. 1957 Teapot effect. J. Appl. Phys. 28, 859–864.Google Scholar
Krechetnikov, R. 2014a Flow around a corner in the water impact problem. Phys. Fluids 26, 072107.Google Scholar
Krechetnikov, R. 2014b Origin of ejecta in the water impact problem. Phys. Fluids 26, 052105.Google Scholar
Krechetnikov, R. 2018 Physics of singularities in pressure-impulse theory. Phys. Rev. Fluids 3, 054003.Google Scholar
Landau, L. D. & Lifshitz, E. M. 1987 Fluid Mechanics. Pergamon.Google Scholar
Lavrentiev, M. A. & Schabat, B. V. 1967 Methoden der Komplexen Funktionentheorie. Deutscher Verlag der Wissenschaften.Google Scholar
Lee, M., Longoria, R. G. & Wilson, D. E. 1997 Cavity dynamics in high-speed water entry. Phys. Fluids 9, 540–550.Google Scholar
LeGoff, A., Quere, D. & Clanet, C. 2013 Viscous cavities. Phys. Fluids 25, 043101.Google Scholar
Leng, L. J. 2001 Splash formation by spherical drops. J. Fluid Mech. 427, 73–105.Google Scholar
Lewison, G. & Maclean, W. M. 1968 On the cushioning of water impact by entrapped air. J. Ship Res. 12, 116–130.Google Scholar
Li, E. Q. & Thoroddsen, S. T. 2015 Time-resolved imaging of a compressible air disc under a drop impacting on a solid surface. J. Fluid Mech. 780, 636–648.Google Scholar
Lin, M. C. & Shieh, L. D. 1997a Flow visualization and pressure characteristics of a cylinder for water impact. Appl. Ocean Res. 19, 101–112.Google Scholar
Lin, M. C. & Shieh, L. D. 1997b Simultaneous measurements of water impact on a two-dimensional body. Fluid Dyn. Res. 19, 125–148.Google Scholar
Liu, Y., Tan, P. & Xu, L. 2013 Compressible air entrapment in high-speed drop impacts on solid surfaces. J. Fluid Mech. 716, R9.Google Scholar
Logvinovich, G. V. 1973 Hydrodynamics of Free Boundary Flows. Israel Program for Scientific Translations.Google Scholar
Logvinovich, G. V. & Yakimov, Y. L. 1973 Submergence of bodies in liquid with large velocities. In Proceedings of the International IUTAM Symposium on Non-Steady Flow of Water at High Speed (ed. Sedov, L. & Stepanov, G. Y.), pp. 85–92. Nauka.Google Scholar
Loitsyanskii, L. G. 1966 Mechanics of Liquids and Gases. Pergamon.Google Scholar
Marston, J. O., Vakarelski, I. U. & Thoroddsen, S. T. 2011 Bubble entrapment during sphere impact onto quiescent liquid surfaces. J. Fluid Mech. 680, 660–670.Google Scholar
Mikhlin, S. G. 1964 Integral Equations. Pergamon.Google Scholar
Moffatt, H. K. 1964 Viscous and resistive eddies near a sharp corner. J. Fluid Mech. 18, 1–18.Google Scholar
Moldovan, A., Bota, M., Boerasu, I., Dorobantu, B., Bojin, D., Buzatu, D. & Enachescu, M. 2013 Wetting properties of glycerol on mica and stainless steel by scanning polarization force microscopy. J. Opt. Adv. Mater. 15, 1101–1105.Google Scholar
Nila, A., Vepa, S., Vanlanduit, S. & Paepegem, W. V. 2013 A PIV-based method for estimating slamming loads during water entry of rigid bodies. Meas. Sci. Technol. 24, 045303.Google Scholar
Oliver, J. M.2002 Water entry and related problems. PhD thesis, University of Oxford.Google Scholar
Ostapenko, V. V. & Kovyrkina, O. A. 2017 Wave flows induced by lifting of a rectangular beam partly immersed in shallow water. J. Fluid Mech. 816, 442–467.Google Scholar
Panciroli, R. & Porfiri, M. 2013 Evaluation of the pressure field on a rigid body entering a quiescent fluid through particle image velocimetry. Exp. Fluids 54, 1630.Google Scholar
Peseux, B., Gornet, L. & Donguy, B. 2005 Hydrodynamic impact: numerical and experimental investigations. J. Fluids Struct. 21, 277–303.Google Scholar
Peters, I. R., van der Meer, D. & Gordillo, J. M. 2013 Splash wave and crown breakup after disc impact on a liquid surface. J. Fluid Mech. 724, 553–580.Google Scholar
Prosperetti, A. & Oguz, H. N. 1997 Air entrainment upon liquid impact. Phil. Trans. R. Soc. Lond. A 355, 491–506.Google Scholar
Pumphrey, H. C. & Elmore, P. A. 1990 The entrainment of bubbles by drop impacts. J. Fluid Mech. 220, 539–567.Google Scholar
Richardson, E. G. 1948 The impact of a solid on a liquid surface. Proc. Phys. Soc. 61, 352–367.Google Scholar
Savva, N. & Bush, J. W. M. 2009 Viscous sheet retraction. J. Fluid Mech. 626, 211–240.Google Scholar
Sedov, L. I. 1965 Two-dimensional Problems of Hydrodynamics and Aerodynamics. Interscience.Google Scholar
Semenov, Y. A. & Wu, G. X. 2018 Water entry of a wedge with rolled-up vortex sheet. J. Fluid Mech. 835, 512–539.Google Scholar
Szebehely, V. G. 1960 Hydrodynamic impact. J. Am. Soc. Nav. Engrs 72, 137–142.Google Scholar
Taylor, G. I. 1959 The dynamics of thin sheets of fluid. III. Disintegration of fluid sheets. Proc. R. Soc. Lond. A 253, 313–321.Google Scholar
Thoroddsen, S. T., Etoh, T. G. & Takehara, K. 2003 Air entrapment under an impacting drop. J. Fluid Mech. 478, 125–134.Google Scholar
Vandre, E., Carvalho, M. S. & Kumar, S. 2014 Characteristics of air entrainment during dynamic wetting failure along a planar substrate. J. Fluid Mech. 747, 119–140.Google Scholar
Verhagen, J. H. G. 1967 Impact of a flat plate on a water surface. J. Ship Res. 11, 211–223.Google Scholar
Wilson, S. K. 1991 A mathematical model for the initial stages of fluid impact in the presence of a cushioning fluid layer. J. Engr. Math. 25, 265–285.Google Scholar
Yakimov, Yu. L. 1973 Influence of atmosphere at falling of bodies on water. Izv. Akad. Nauk SSSR Mekh. Zhidk. Gaza 5, 3–6.Google Scholar
Zhao, R., Faltinsen, O. M. & Aarnes, J. 1996 Water entry of arbitrary two-dimensional sections with and without flow separation. In Proceedings of the 21st International Symposium on Naval Hydrodynamics (ed. Rood, E.), pp. 118–132. Trondheim.Google Scholar