Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Govindarajan, Rama
and
Sahu, Kirti Chandra
2014.
Instabilities in Viscosity-Stratified Flow.
Annual Review of Fluid Mechanics,
Vol. 46,
Issue. 1,
p.
331.
Peplinski, A.
Schlatter, P.
Fischer, P. F.
and
Henningson, D. S.
2014.
Spectral and High Order Methods for Partial Differential Equations - ICOSAHOM 2012.
Vol. 95,
Issue. ,
p.
349.
Luchini, Paolo
and
Bottaro, Alessandro
2014.
Adjoint Equations in Stability Analysis.
Annual Review of Fluid Mechanics,
Vol. 46,
Issue. 1,
p.
493.
Carini, M.
Giannetti, F.
and
Auteri, F.
2014.
On the origin of the flip–flop instability of two side-by-side cylinder wakes.
Journal of Fluid Mechanics,
Vol. 742,
Issue. ,
p.
552.
Carini, M.
Giannetti, F.
and
Auteri, F.
2014.
First instability and structural sensitivity of the flow past two side-by-side cylinders.
Journal of Fluid Mechanics,
Vol. 749,
Issue. ,
p.
627.
Citro, Vincenzo
Giannetti, Flavio
and
Pralits, Jan O
2015.
Three-dimensional stability, receptivity and sensitivity of non-Newtonian flows inside open cavities.
Fluid Dynamics Research,
Vol. 47,
Issue. 1,
p.
015503.
Camarri, Simone
2015.
Flow control design inspired by linear stability analysis.
Acta Mechanica,
Vol. 226,
Issue. 4,
p.
979.
Pantokratoras, Asterios
2015.
Non-similar Blasius and Sakiadis flow of a non-Newtonian Carreau fluid.
Journal of the Taiwan Institute of Chemical Engineers,
Vol. 56,
Issue. ,
p.
1.
Pantokratoras, Asterios
2016.
Steady flow of a non-Newtonian Carreau fluid across an unconfined circular cylinder.
Meccanica,
Vol. 51,
Issue. 4,
p.
1007.
Griffiths, P. T.
Gallagher, M. T.
and
Stephen, S. O.
2016.
The effect of non-Newtonian viscosity on the stability of the Blasius boundary layer.
Physics of Fluids,
Vol. 28,
Issue. 7,
Carini, M.
Airiau, C.
Debien, A.
Léon, O.
and
Pralits, J. O.
2017.
Global stability and control of the confined turbulent flow past a thick flat plate.
Physics of Fluids,
Vol. 29,
Issue. 2,
Vázquez-Quesada, A.
Wagner, N. J.
and
Ellero, M.
2017.
Planar channel flow of a discontinuous shear-thickening model fluid: Theory and simulation.
Physics of Fluids,
Vol. 29,
Issue. 10,
Chatterjee, Ajay
and
Fabris, Drazen
2017.
Planar non-Newtonian confined laminar impinging jets: Hysteresis, linear stability, and periodic flow.
Physics of Fluids,
Vol. 29,
Issue. 10,
Sun, Chen-li
Lin, Yu Jen
Rau, Chia-I
and
Chiu, Shao-Yu
2017.
Flow characterization and mixing performance of weakly-shear-thinning fluid flows in a microfluidic oscillator.
Journal of Non-Newtonian Fluid Mechanics,
Vol. 239,
Issue. ,
p.
1.
Khan, Masood
Sardar, Humara
Gulzar, M. Mudassar
and
Alshomrani, Ali Saleh
2018.
On multiple solutions of non-Newtonian Carreau fluid flow over an inclined shrinking sheet.
Results in Physics,
Vol. 8,
Issue. ,
p.
926.
Zhao, Lifei
Li, Zhen
Caswell, Bruce
Ouyang, Jie
and
Karniadakis, George Em
2018.
Active learning of constitutive relation from mesoscopic dynamics for macroscopic modeling of non-Newtonian flows.
Journal of Computational Physics,
Vol. 363,
Issue. ,
p.
116.
Kim, Namhee
and
Reddy, J. N.
2018.
Least-squares finite element analysis of flow of a generalized Newtonian fluid past a circular cylinder.
Mechanics of Advanced Materials and Structures,
Vol. 25,
Issue. 14,
p.
1186.
Şahin, Çağlar
and
Atalık, Kunt
2019.
Comparison of inelastic and elastic non-Newtonian effects on the flow around a circular cylinder in periodic vortex shedding.
Journal of Non-Newtonian Fluid Mechanics,
Vol. 263,
Issue. ,
p.
1.
Deteix, J.
and
Yakoubi, D.
2019.
Shear rate projection schemes for non-Newtonian fluids.
Computer Methods in Applied Mechanics and Engineering,
Vol. 354,
Issue. ,
p.
620.
Lee, Junseong
Kim, Junkyu
Lim, Jiseop
Yun, Yeji
Kim, Youngho
Ryu, Jeha
and
Jee, Solkeun
2019.
Unsteady flow of shear-thickening fluids around an impulsively moving circular cylinder.
Journal of Non-Newtonian Fluid Mechanics,
Vol. 272,
Issue. ,
p.
104163.
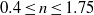 and
and 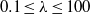 . We show how shear-thinning/shear-thickening effects destabilize/stabilize the flow dramatically when scaling the problem with the reference zero-shear-rate viscosity. These variations are explained by modifications of the steady base flow due to the shear-dependent viscosity; the instability mechanisms are only slightly changed. The characteristics of the base flow, drag coefficient and size of recirculation bubble are presented to assess shear-thinning effects. We demonstrate that at critical conditions the local Reynolds number in the core of the instability is around 50 as for Newtonian fluids. The perturbation kinetic energy budget is also considered to examine the physical mechanism of the instability.
. We show how shear-thinning/shear-thickening effects destabilize/stabilize the flow dramatically when scaling the problem with the reference zero-shear-rate viscosity. These variations are explained by modifications of the steady base flow due to the shear-dependent viscosity; the instability mechanisms are only slightly changed. The characteristics of the base flow, drag coefficient and size of recirculation bubble are presented to assess shear-thinning effects. We demonstrate that at critical conditions the local Reynolds number in the core of the instability is around 50 as for Newtonian fluids. The perturbation kinetic energy budget is also considered to examine the physical mechanism of the instability.

