Hostname: page-component-7479d7b7d-qs9v7 Total loading time: 0 Render date: 2024-07-12T09:23:58.875Z Has data issue: false hasContentIssue false
  • English
  • Français

Finite wavelength selection for the linear instability of a suspension of settling spheroids

Published online by Cambridge University Press:  07 November 2011

Anders A. Dahlkild
Anders A. Dahlkild*
Affiliation:
Linné Flow Centre, Department of Mechanics, KTH, 100 44 Stockholm, Sweden
*
†Email address for correspondence: ad@mech.kth.se
Get access Rights & Permissions [Opens in a new window]

Abstract

The instability of an initially homogeneous suspension of spheroids, settling due to gravity, is reconsidered. For non-spherical particles, previous studies in the literature report that normal-mode density perturbations of maximum growth rate are those of arbitrarily large, horizontal wavelength. Using the ‘mixture theory’ for two-phase flow we show that the maximum growth rate for horizontal density perturbations is obtained for a finite wavelength if the inertia of the bulk motion associated with the normal-mode density perturbation is accounted for. We find that for long wavelengths, 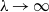, the growth rate approaches zero as 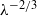. The maximum growth rate is obtained for 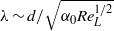, where 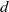is the axis perpendicular to the axis of rotational symmetry of the spheroid, is the undisturbed volume fraction of particles and 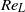, typically 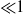, is a Reynolds number of the bulk motion on a typical length scale and a velocity scale on the order of the undisturbed settling speed. The theoretical results for the wavelength selection agree qualitatively well with previous experimental results in the literature of measured correlation lengths of vertical streamers in settling fibre suspensions.

JFM classification

Instability: Instability Multiphase and Particle-laden Flows: Particle/fluid flow
Type
Papers
Information
Journal of Fluid Mechanics , Volume 689 , 25 December 2011 , pp. 183 - 202
Copyright
Copyright © Cambridge University Press 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Batchelor, G. K. 1970 Slender-body theory for particles of arbitrary cross-section in Stokes flow. J. Fluid Mech. 44, 419–440.CrossRefGoogle Scholar
2. Butler, J. E. & Shaqfeh, E. S. G. 2002 Dynamic simulations of the inhomogeneous sedimentation of rigid fibres. J. Fluid Mech. 468, 205–237.Google Scholar
3. Guazzelli, É. & Hinch, J. 2011 Fluctuations and instability in sedimentation. Annu. Rev. Fluid Mech. 43, 97–116.CrossRefGoogle Scholar
4. Happel, J. & Brenner, H. 1965 Low Reynolds Number Hydrodynamics. Prentice-Hall.Google Scholar
5. Herzhaft, B. & Guazzelli, É 1999 Experimental study of the sedimentation of dilute and semi-dilute suspensions of fibres. J. Fluid Mech. 384, 133–158.CrossRefGoogle Scholar
6. Herzhaft, B., Guazzelli, É, Mackaplow, M. B. & Shaqfeh, E. S. G. 1996 Experimental investigation of the sedimentation of a dilute fibre suspension. Phys. Rev. Lett. 77 (2), 290–293.Google Scholar
7. Ishii, M. 1975 Thermo-Fluid Dynamic Theory of Two-Phase Flow. Eyrolles.Google Scholar
8. Jeffrey, G. B. 1922 The motion of ellipsoidal particles immersed in a viscous fluid. Proc. R. Soc. A102, 161–179.Google Scholar
9. Koch, D. L. & Shaqfeh, E. S. G. 1989 The instability of a dispersion of sedimenting spheroids. J. Fluid Mech. 209, 521–542.CrossRefGoogle Scholar
10. Kumar, P. & Ramaro, B. V. 1991 Enhancement of the sedimentation rates in fibrous suspensions. Chem. Engng Commun. 108, 381–401.CrossRefGoogle Scholar
11. Kuusela, E., Lahtinen, J. M. & Ala-Nissila, T. 2005 Collective effects in settling of spheroids under steady-state sedimentation. Phys. Rev. Lett. 90, 094502.CrossRefGoogle Scholar
12. Mackaplow, M. B. & Shaqfeh, E. S. G. 1998 A numerical study of the sedimentation of fibre suspensions. J. Fluid Mech. 376, 149–182.CrossRefGoogle Scholar
13. Metzger, B., Butler, J. E. & Guazzelli, É 2007a Experimental investigation of the instability of a sedimenting suspension of fibres. J. Fluid Mech. 575, 307–332.CrossRefGoogle Scholar
14. Metzger, B., Butler, J. E. & Guazzelli, É 2007b On wavelength selection by stratification in the instability of settling fibres. Phys. Fluids 19, 098105.CrossRefGoogle Scholar
15. Metzger, B., Guazzelli, É & Butler, J. E. 2005 Large-scale streamers in the sedimentation of a dilute fibre suspension. Phys. Rev. Lett. 95, 164506.CrossRefGoogle ScholarPubMed
16. Narsimhan, V. & Shaqfeh, E. S. G. 2010 Lateral drift and concentration instability in a suspension of bubbles induced by Marangoni stresses at zero Reynolds number. Phys. Fluids 22, 101702.CrossRefGoogle Scholar
17. Saintillian, D., Darve, E. & Shaqfeh, E. S. G. 2005 A smooth particle-mesh Ewald algorithm for Stokes suspension simulations: the sedimentation of fibres. Phys. Fluids 17, 033301.CrossRefGoogle Scholar
18. Saintillian, D., Shaqfeh, E. S. G. & Darve, E. 2006a The growth of concentration fluctuations in dilute dispersions of orientable and deformable particles under sedimentation. J. Fluid Mech. 553, 347–388.CrossRefGoogle Scholar
19. Saintillian, D., Shaqfeh, E. S. G. & Darve, E. 2006b The effect of stratification on the wavenumber selection in the instability of sedimenting spheroids. Phys. Fluids 18, 121503.Google Scholar
20. Shin, M., Koch, D. L. & Subramanian, G. 2009 Structure and dynamics of dilute suspensions of finite-Reynolds number settling fibres. Phys. Fluids 21, 123304.CrossRefGoogle Scholar
21. Tornberg, A.-K. & Gustavsson, K. 2006 A numerical method for simulations of rigid fibre suspensions. J. Comput. Phys. 215, 172–196.Google Scholar
22. Ungarish, M. 1993 Hydrodynamics of Suspensions. Springer.Google Scholar