Article contents
Extensional and shear flows, and general rheology of concentrated emulsions of deformable drops
Published online by Cambridge University Press: 14 August 2015
Abstract
The rheology of highly concentrated monodisperse emulsions is studied by rigorous multidrop numerical simulations for three types of steady macroscopic flow, (i) simple shear (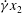 $\dot{{\it\gamma}}x_{2}$, 0 0), (ii) planar extension (PE) (
$\dot{{\it\gamma}}x_{2}$, 0 0), (ii) planar extension (PE) ( $\dot{{\it\Gamma}}x_{1},-\dot{{\it\Gamma}}x_{2},0$) and (iii) mixed (
$\dot{{\it\Gamma}}x_{1},-\dot{{\it\Gamma}}x_{2},0$) and (iii) mixed (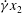 $\dot{{\it\gamma}}x_{2}$,
$\dot{{\it\gamma}}x_{2}$, 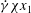 $\dot{{\it\gamma}}{\it\chi}x_{1}$, 0), where
$\dot{{\it\gamma}}{\it\chi}x_{1}$, 0), where 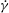 $\dot{{\it\gamma}}$ and
$\dot{{\it\gamma}}$ and 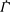 $\dot{{\it\Gamma}}$ are the deformation rates, and
$\dot{{\it\Gamma}}$ are the deformation rates, and 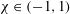 ${\it\chi}\in (-1,1)$ is the flow parameter, in order to construct and validate a general constitutive model for emulsion flows with arbitrary kinematics. The algorithm is a development of the multipole-accelerated boundary-integral (BI) code of Zinchenko & Davis (J. Fluid Mech., vol. 455, 2002, pp. 21–62). It additionally incorporates periodic boundary conditions for (ii) and (iii) (based on the reproducible lattice dynamics of Kraynik–Reinelt for PE), control of surface overlapping, much more robust controllable surface triangulations for long-time simulations, and more efficient acceleration. The emulsion steady-state viscometric functions (shear viscosity and normal stress differences) for (i) and extensiometric functions (extensional viscosity and stress cross-difference) for (ii) are studied in the range of drop volume fractions
${\it\chi}\in (-1,1)$ is the flow parameter, in order to construct and validate a general constitutive model for emulsion flows with arbitrary kinematics. The algorithm is a development of the multipole-accelerated boundary-integral (BI) code of Zinchenko & Davis (J. Fluid Mech., vol. 455, 2002, pp. 21–62). It additionally incorporates periodic boundary conditions for (ii) and (iii) (based on the reproducible lattice dynamics of Kraynik–Reinelt for PE), control of surface overlapping, much more robust controllable surface triangulations for long-time simulations, and more efficient acceleration. The emulsion steady-state viscometric functions (shear viscosity and normal stress differences) for (i) and extensiometric functions (extensional viscosity and stress cross-difference) for (ii) are studied in the range of drop volume fractions 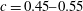 $c=0.45{-}0.55$, drop-to-medium viscosity ratios
$c=0.45{-}0.55$, drop-to-medium viscosity ratios 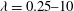 ${\it\lambda}=0.25{-}10$ and various capillary numbers
${\it\lambda}=0.25{-}10$ and various capillary numbers 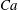 $\mathit{Ca}$, with 100–400 drops in a periodic cell and 2000–4000 boundary elements per drop. High surface resolution is important for all three flows at small
$\mathit{Ca}$, with 100–400 drops in a periodic cell and 2000–4000 boundary elements per drop. High surface resolution is important for all three flows at small 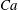 $\mathit{Ca}$. Large system size and strains
$\mathit{Ca}$. Large system size and strains 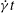 $\dot{{\it\gamma}}t$ of up to several thousand are imperative in some shear-flow simulations to identify the onset of phase transition to a partially ordered state, and evaluate (although still not precisely) the viscometric functions in this state. Below the phase transition point, the shear viscosity versus
$\dot{{\it\gamma}}t$ of up to several thousand are imperative in some shear-flow simulations to identify the onset of phase transition to a partially ordered state, and evaluate (although still not precisely) the viscometric functions in this state. Below the phase transition point, the shear viscosity versus 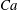 $\mathit{Ca}$ shows a kinked behaviour, with the local minimum most pronounced at
$\mathit{Ca}$ shows a kinked behaviour, with the local minimum most pronounced at 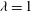 ${\it\lambda}=1$ and
${\it\lambda}=1$ and 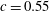 $c=0.55$. The
$c=0.55$. The 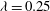 ${\it\lambda}=0.25$ emulsions flow in a partially ordered manner in a wide range of
${\it\lambda}=0.25$ emulsions flow in a partially ordered manner in a wide range of 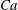 $\mathit{Ca}$ even when
$\mathit{Ca}$ even when 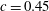 $c=0.45$. Increase of
$c=0.45$. Increase of 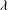 ${\it\lambda}$ to 3–10 shifts the onset of ordering to much smaller
${\it\lambda}$ to 3–10 shifts the onset of ordering to much smaller 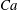 $\mathit{Ca}$, often outside the simulation range. In contrast to simple shear, phase transition is never observed in PE or mixed flow. A generalized five-parameter Oldroyd model with variable coefficients is fitted to our extensiometric and viscometric functions at arbitrary flow intensities (but outside the phase transition range). The model predictions compare very well with precise simulation results for strong mixed flows,
$\mathit{Ca}$, often outside the simulation range. In contrast to simple shear, phase transition is never observed in PE or mixed flow. A generalized five-parameter Oldroyd model with variable coefficients is fitted to our extensiometric and viscometric functions at arbitrary flow intensities (but outside the phase transition range). The model predictions compare very well with precise simulation results for strong mixed flows, 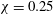 ${\it\chi}=0.25$. Time-dependent PE flow is also considered. Ways to overcome the phase transition and drop breakup limitations on constitutive modelling are discussed.
${\it\chi}=0.25$. Time-dependent PE flow is also considered. Ways to overcome the phase transition and drop breakup limitations on constitutive modelling are discussed.
- Type
- Papers
- Information
- Copyright
- © 2015 Cambridge University Press
References
- 18
- Cited by



