Hostname: page-component-8448b6f56d-c4f8m Total loading time: 0 Render date: 2024-04-16T14:40:28.881Z Has data issue: false hasContentIssue false
  • English
  • Français

Extended series solutions and bifurcations of the Dean equations

Published online by Cambridge University Press:  17 December 2013

F. A. T. Boshier  and
A. J. Mestel
F. A. T. Boshier
Affiliation:
Department of Mathematics, Imperial College London, London SW7 2RH, UK
A. J. Mestel*
Affiliation:
Department of Mathematics, Imperial College London, London SW7 2RH, UK
*
†Email address for correspondence: j.mestel@ic.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

Steady, incompressible flow down a slowly curving circular pipe is considered. Both real and complex solutions of the Dean equations are found by analytic continuation of a series expansion in the Dean number, 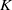$K$. Higher-order Hermite–Padé approximants are used and the results compared with direct computations using a spectral method. The two techniques agree for large, real 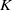$K$, indicating that previously reported asymptotic behaviour of the series solution is incorrect, and thus resolving a long-standing paradox. It is further found that a second solution branch, known to exist at high Dean number, does not appear to merge with the main branch at any finite 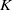$K$, but appears rather to bifurcate from infinity. The convergence of the series is limited by a square-root singularity on the imaginary 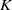$K$-axis. Four complex solutions merge at this point. One corresponds to an extension of the real solution, while the other three are previously unreported. This bifurcation is found to coincide with the breaking of a symmetry property of the flow. On one of the new branches the velocity is unbounded as 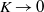$K\rightarrow 0$. It follows that the zero-Dean-number flow is formally non-unique, in that there is a second complex solution as 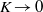$K\rightarrow 0$ for any non-zero 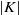$\vert K\vert $. This behaviour is manifested in other flows at zero Reynolds number. The other two complex solutions bear some resemblance to the two solution branches for large real 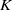$K$.

JFM classification

Nonlinear Dynamical Systems: Bifurcation Nonlinear Dynamical Systems: Nonlinear Dynamical Systems
Type
Papers
Information
Journal of Fluid Mechanics , Volume 739 , 25 January 2014 , pp. 179 - 195
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adler, M. 1934 Stromung in gekrummten Rohren. Z. Angew. Math. Mech. 14, 257–275.Google Scholar
Agrawal, Y., Talbot, L. & Gong, K. 1978 Laser anemometer study of flow development in curved circular pipes. J. Fluid Mech. 85, 497–518.Google Scholar
Barua, S. N. 1963 On secondary flow in stationary curved pipes. Q. J. Mech. Appl. Maths 16, 61–77.Google Scholar
Conway, B. A. 1978 Extension of Stokes series for flow in a circular boundary. Phys. Fluids 21, 289–290.Google Scholar
Daskopoulos, P. & Lenhoff, A. M. 1989 Flow in curved ducts: bifurcation structure for stationary ducts. J. Fluid Mech. 203, 125–148.Google Scholar
Dean, W. R. 1927 Note on the motion of fluid in a curved pipe. Phil. Mag. 28, 208–223.Google Scholar
Dean, W. R. 1928 The stream-line motion of fluid in a curved pipe. Phil. Mag. 5, 673–695.Google Scholar
Dennis, S. C. R. 1980 Calculation of the steady flow through a curved tube using a new finite difference method. J. Fluid Mech. 99, 449–467.CrossRefGoogle Scholar
Dennis, S. C. R & Ng, M. 1982 Dual solutions for steady laminar flow through a curved tube. Q. J. Mech. Appl. Maths 35 (3), 305–324.Google Scholar
Dennis, S. C. R. & Riley, N. 1991 On the fully developed flow in a curved pipe at large Dean number. Proc. R. Soc. Lond. (A) 434, 473–478.Google Scholar
Domb, C. & Sykes, M. F. 1957 On the susceptability of the ferromagnetic above the Curie point. Proc. R. Soc. Lond. (A) 240, 214–228.Google Scholar
Drazin, P. G. & Tourigny, Y. 1996 Numerical study of bifurcations by analytic continuation of a function defined by a power series. SIAM J. Appl. Maths 56, 1–18.Google Scholar
Gaunt, D. S. & Guttmann, A. J. 1974 Series Expansions: analysis of coefficients. In Phase Transitions and Critical Phenomena, vol. 3, Academic.Google Scholar
GMP Team 2008 The GNU Multiple Precision Arithmetic Library.Google Scholar
Hasson, D. 1955 Streamline flow resistance in coils. Res. Corresp. 1, S1.Google Scholar
Henderson, M. E. & Keller, H. B. 1990 Complex bifurcation from real paths. SIAM J. Appl. Maths 50 (2), 460–482.Google Scholar
Hoffman, G. H. 1974 Extension of perturbation series by computer: viscous flow between two infinite rotating disks. J. Comput. Phys. 16, 240–258.Google Scholar
Hunter, C. 1987 Oscillations in the coefficients of power series. SIAM J. Appl. Maths 47 (3), 483–497.Google Scholar
Ito, H. 1968 Laminar flow in curved pipes. Z. Angew. Math. Mech. 49, 653–663.CrossRefGoogle Scholar
Jayanti, S. & Hewitt, G. F. 1991 On the paradox concerning friction factor ratio in laminar flow in coils. Proc. Math. Phys. Sci. 432, 291–299.Google Scholar
Mansour, K. 1985 Laminar flow through a slowly rotating straight pipe. J. Fluid Mech. 150, 1–21.Google Scholar
Mansour, K. 1993 Using Stokes expansion for natural convection inside a two-dimensional cavity. Fluid Dyn. Res. 23, 1–33.Google Scholar
Pedley, T. J 1980 The Fluid Mechanics of Large Blood Vessels. Cambridge University Press.Google Scholar
Ramshankar, R. & Sreenivasan, K. R. 1988 A paradox concerning the extended Stokes series solution for the pressure drop in coiled pipes. Phys. Fluids 31, 1339–1347.Google Scholar
Siggers, J. H. & Waters, S. L. 2005 Steady flow in pipes with finite curvature. Phys. Fluids 17 (7), 077102.Google Scholar
Smith, F. T. 1976 Steady motion within a curved pipe. Proc. R. Soc. Lond. (A) Mathematical and Physical Sciences 347 (1650), 345–370.Google Scholar
Tettamanti, F. A. 2012 Extended Stokes series for Dean flow in weakly curved pipes. PhD thesis, Imperial College London.Google Scholar
Van Dyke, M. 1974 Analysis and improvement of perturbation series. Q. J. Mech. Appl. Maths 27, 423–450.Google Scholar
Van Dyke, M. 1978 Extended Stokes series: laminar flow through a loosely coiled pipe. J. Fluid Mech. 86, 129–145.Google Scholar
Van Dyke, M. 1984 Computer-extended series. Annu. Rev. Fluid Mech. 16, 287–309.Google Scholar
Van Dyke, M. 1989 Some paradoxes in viscous flow theory. In Some Unanswered Questions in Fluid Mecahnics, Applied Mechanics Reviews, 43, pp. 153–170.Google Scholar
Van Dyke, M. 1990 Extended Stokes series: laminar flow through a heated horizontal pipe. J. Fluid Mech. 212, 289–308.Google Scholar
Yang, Z. & Keller, H. B. 1986 Multiple laminar flows through curved pipes. Appl. Numer. Maths 2, 257–271.Google Scholar