Hostname: page-component-76fb5796d-25wd4 Total loading time: 0 Render date: 2024-04-26T14:20:53.947Z Has data issue: false hasContentIssue false
  • English
  • Français

Experimental investigation of the acceleration statistics and added-mass force of deformable bubbles in intense turbulence

Published online by Cambridge University Press:  18 February 2021

Ashwanth K.R. Salibindla ,
Ashik Ullah Mohammad Masuk  and
Rui Ni Open the ORCID record for Rui Ni [Opens in a new window]
Ashwanth K.R. Salibindla
Affiliation:
Department of Mechanical Engineering, Johns Hopkins University, Baltimore, MD21210, USA
Ashik Ullah Mohammad Masuk
Affiliation:
Department of Mechanical Engineering, Johns Hopkins University, Baltimore, MD21210, USA
Rui Ni*
Affiliation:
Department of Mechanical Engineering, Johns Hopkins University, Baltimore, MD21210, USA
*
†Email address for correspondence: rui.ni@jhu.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

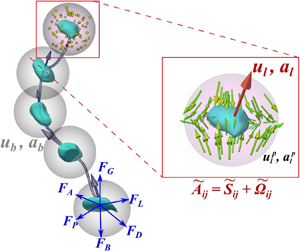
We present an experimental investigation of the acceleration statistics and the added mass tensor of deformable gas bubbles in turbulence. By simultaneously tracking both bubbles and their surrounding flow in three dimensions, we find two independent ways of estimating the bubble acceleration: either directly measured from three-dimensional bubble trajectories or indirectly calculated from the bubble's equation of motion. When such an equation is projected onto the bubble frame, the added-mass coefficient becomes a diagonal tensor with three elements being linked to the standard deviation of bubble acceleration along three bubble principal axes. This constraint aids in experimentally determining the added mass coefficient tensor. The obtained trend of $C_A$ seems to agree with Lamb's potential flow solutions for spheroids, suggesting that the added-mass force on deformable bubbles can be modelled using spheroids with the same geometry and orientation. In addition, the probability density function of the relative orientation between the semi-major axis of deformed bubbles and the slip acceleration in turbulence is shown. A surprising finding is that the bubble orientation, indicated by the bubble's major axis, is not random in turbulence but rather is preferentially aligned with the slip acceleration. The degree of this alignment increases as bubbles deform more. Because accelerating along the major axis of a more deformed bubble entails reduced added mass, the acceleration standard deviation of deformable bubbles increases as a function of the bubble aspect ratio.

JFM classification

Drops and Bubbles: Bubble dynamics Multiphase and Particle-laden Flows: Multiphase flow Turbulent Flows: Isotropic turbulence
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 912 , 10 April 2021 , A50
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Alméras, E., Mathai, V., Sun, C. & Lohse, D. 2019 Mixing induced by a bubble swarm rising through incident turbulence. Intl J. Multiphase Flow 114, 316–322.CrossRefGoogle Scholar
Batchelor, C.K. 1967 An Introduction to Fluid Dynamics. Cambridge University Press.Google Scholar
Brennen, C.E. 1982 A review of added mass and fluid inertial forces. Tech. Rep. CR 82.010. Brennen (CE), Sierra Madre, CA.Google Scholar
Brown, R.D., Warhaft, Z. & Voth, G.A. 2009 Acceleration statistics of neutrally buoyant spherical particles in intense turbulence. Phys. Rev. Lett. 103 (19), 194501.CrossRefGoogle ScholarPubMed
Calzavarini, E., Volk, R., Lévêque, E., Pinton, J.-F. & Toschi, F. 2012 Impact of trailing wake drag on the statistical properties and dynamics of finite-sized particle in turbulence. Physica D 241 (3), 237–244.CrossRefGoogle Scholar
Cano-Lozano, J.C., Martinez-Bazan, C., Magnaudet, J. & Tchoufag, J. 2016 Paths and wakes of deformable nearly spheroidal rising bubbles close to the transition to path instability. Phys. Rev. Fluids 1 (5), 053604.CrossRefGoogle Scholar
Chang, E.J. & Maxey, M.R. 1994 Unsteady flow about a sphere at low to moderate Reynolds number. Part 1. Oscillatory motion. J. Fluid Mech. 277, 347–379.CrossRefGoogle Scholar
Chang, E.J. & Maxey, M.R. 1995 Unsteady flow about a sphere at low to moderate Reynolds number. Part 2. Accelerated motion. J. Fluid Mech. 303, 133–153.CrossRefGoogle Scholar
De Vries, J., Luther, S. & Lohse, D. 2002 Induced bubble shape oscillations and their impact on the rise velocity. Eur. Phys. J. B 29 (3), 503–509.CrossRefGoogle Scholar
Deane, G.B. & Stokes, M.D. 2002 Scale dependence of bubble creation mechanisms in breaking waves. Nature 418 (6900), 839–844.CrossRefGoogle ScholarPubMed
Du Cluzeau, A., Bois, G. & Toutant, A. 2019 Analysis and modelling of Reynolds stresses in turbulent bubbly up-flows from direct numerical simulations. J. Fluid Mech. 866, 132–168.CrossRefGoogle Scholar
Fernandes, P.C., Ern, P., Risso, F. & Magnaudet, J. 2008 Dynamics of axisymmetric bodies rising along a zigzag path. J. Fluid Mech. 606, 209–223.CrossRefGoogle Scholar
Friedman, P.D. & Katz, J. 2002 Mean rise rate of droplets in isotropic turbulence. Phys. Fluids 14 (9), 3059–3073.CrossRefGoogle Scholar
Howe, M.S. 1995 On the force and moment on a body in an incompressible fluid, with application to rigid bodies and bubbles at high and low reynolds numbers. Q. J. Mech. Appl. Maths 48 (3), 401–426.CrossRefGoogle Scholar
Jakobsen, H.A. 2008 Chemical reactor modeling. Multiphase Reactive Flows.Google Scholar
Kendoush, A.A., Sulaymon, A.H. & Mohammed, S.A.M. 2007 Experimental evaluation of the virtual mass of two solid spheres accelerating in fluids. Exp. Therm. Fluid Sci. 31 (7), 813–823.CrossRefGoogle Scholar
Lamb, H. 1924 Hydrodynamics. University Press.Google Scholar
Lavrenteva, O., Prakash, J. & Nir, A. 2016 Effect of added mass on the interaction of bubbles in a low-Reynolds-number shear flow. Phys. Rev. E 93 (2), 023105.CrossRefGoogle Scholar
Loisy, A. & Naso, A. 2017 Interaction between a large buoyant bubble and turbulence. Phys. Rev. Fluids 2 (1), 014606.CrossRefGoogle Scholar
Magnaudet, J. 1997 The forces acting on bubbles and rigid particles. In ASME Fluids Engineering Division Summer Meeting, FEDSM, vol. 97, pp. 22–26.Google Scholar
Magnaudet, J. & Eames, I. 2000 The motion of high-Reynolds-number bubbles in inhomogeneous flows. Annu. Rev. Fluid Mech. 32 (1), 659–708.CrossRefGoogle Scholar
Maliska, C.R. & Paladino, E.E. 2006 The role of virtual mass, lift and wall lubrication forces in accelerated bubbly flows. Energy: Production, Distribution Conservation-Milan 2006, 953–962.Google Scholar
Masuk, A.U.M., Qi, Y., Salibindla, A.K.R. & Ni, R. 2020 a A phenomenological model on the deformation and orientation dynamics of finite-sized bubbles in both quiescent and turbulent media. J. Fluid Mech. (submitted).Google Scholar
Masuk, A.U.M., Salibindla, A.K.R. & Ni, R. 2019 a A robust virtual-camera 3D shape reconstruction of deforming bubbles/droplets with additional physical constraints. Intl J. Multiphase Flow 120, 103088.CrossRefGoogle Scholar
Masuk, A.U.M., Salibindla, A.K.R. & Ni, R. 2020 b Simultaneous measurements of deforming Hinze-scale bubbles with surrounding turbulence. J. Fluid Mech. 910, A21.CrossRefGoogle Scholar
Masuk, A.U.M., Salibindla, A.K.R., Tan, S. & Ni, R. 2019 b V-ONSET (vertical octagonal noncorrosive stirred energetic turbulence): a vertical water tunnel with a large energy dissipation rate to study bubble/droplet deformation and breakup in strong turbulence. Rev. Sci. Instrum. 90 (8), 085105.CrossRefGoogle ScholarPubMed
Mathai, V., Calzavarini, E., Brons, J., Sun, C. & Lohse, D. 2016 Microbubbles and microparticles are not faithful tracers of turbulent acceleration. Phys. Rev. Lett. 117 (2), 024501.CrossRefGoogle Scholar
Mathai, V., Lohse, D. & Sun, C. 2020 Bubble and buoyant particle laden turbulent flows. Annu. Rev. Condens. Matter Phys. 11, 529–559.CrossRefGoogle Scholar
Mei, R. & Klausner, J.F. 1992 Unsteady force on a spherical bubble at finite Reynolds number with small fluctuations in the free-stream velocity. Phys. Fluids A 4 (1), 63–70.CrossRefGoogle Scholar
Mei, R., Lawrence, C.J. & Adrian, R.J. 1991 Unsteady drag on a sphere at finite Reynolds number with small fluctuations in the free-stream velocity. J. Fluid Mech. 233, 613–631.CrossRefGoogle Scholar
Michiyoshi, I. & Serizawa, A. 1986 Turbulence in two-phase bubbly flow. Nucl. Engng Des. 95, 253–267.CrossRefGoogle Scholar
Mordant, N., Crawford, A.M. & Bodenschatz, E. 2004 Experimental lagrangian acceleration probability density function measurement. Physica D 193 (1–4), 245–251.CrossRefGoogle Scholar
Mougin, G. & Magnaudet, J. 2006 Wake-induced forces and torques on a zigzagging/spiralling bubble. J. Fluid Mech. 567, 185–194.CrossRefGoogle Scholar
Newman, J.N. 1977 Marine Hydrodynamics. Massachusetts Institute of Technology.CrossRefGoogle Scholar
Ni, R., Huang, S.-D. & Xia, K.-Q. 2012 Lagrangian acceleration measurements in convective thermal turbulence. J. Fluid Mech. 692, 395–419.CrossRefGoogle Scholar
Ni, R., Kramel, S., Ouellette, N.T. & Voth, G.A. 2015 Measurements of the coupling between the tumbling of rods and the velocity gradient tensor in turbulence. J. Fluid Mech. 766, 202–225.CrossRefGoogle Scholar
Prakash, J., Lavrenteva, O.M., Byk, L. & Nir, A. 2013 Interaction of equal-size bubbles in shear flow. Phys. Rev. E 87 (4), 043002.CrossRefGoogle ScholarPubMed
Prakash, V.N., Tagawa, Y., Calzavarini, E., Mercado, J., Toschi, F., Lohse, D. & Sun, C. 2012 How gravity and size affect the acceleration statistics of bubbles in turbulence. New J. Phys. 14 (10), 105017.CrossRefGoogle Scholar
Pudasaini, S.P. 2019 A fully analytical model for virtual mass force in mixture flows. Intl J. Multiphase Flow 113, 142–152.CrossRefGoogle Scholar
Pumir, A., Bodenschatz, E. & Xu, H. 2013 Tetrahedron deformation and alignment of perceived vorticity and strain in a turbulent flow. Phys. Fluids 25 (3), 035101.CrossRefGoogle Scholar
Qureshi, N.M., Bourgoin, M., Baudet, C., Cartellier, A. & Gagne, Y. 2007 Turbulent transport of material particles: an experimental study of finite size effects. Phys. Rev. Lett. 99 (18), 184502.CrossRefGoogle ScholarPubMed
Salibindla, A.K.R., Masuk, A.U.M., Tan, S. & Ni, R. 2020 Lift and drag coefficients of deformable bubbles in intense turbulence determined from bubble rise velocity. J. Fluid Mech. 894, A20.CrossRefGoogle Scholar
Sankaranarayanan, K., Shan, X., Kevrekidis, I.G. & Sundaresan, S. 2002 Analysis of drag and virtual mass forces in bubbly suspensions using an implicit formulation of the lattice Boltzmann method. J. Fluid Mech. 452, 61–96.CrossRefGoogle Scholar
Sarpkaya, T. 1975 Forces on cylinders and spheres in a sinusoidally oscillating fluid. J. Appl. Mech. 42 (1), 32–37.CrossRefGoogle Scholar
Sridhar, G. & Katz, J. 1995 Drag and lift forces on microscopic bubbles entrained by a vortex. Phys. Fluids 7 (2), 389–399.CrossRefGoogle Scholar
Takagi, S. & Matsumoto, Y. 1996 Force acting on a rising bubble in a quiescent liquid. Trans. ASME: Fluids Engng Div. 236, 575–580.Google Scholar
Tan, S., Salibindla, A.K.R., Masuk, A.U.M. & Ni, R. 2019 An open-source Shake-the-Box method and its performance evaluation. In 13th International Symposium on Particle Image Velocimetry – ISPIV 2019.Google Scholar
Tan, S., Salibindla, A.K.R., Masuk, A.U.M. & Ni, R. 2020 Introducing openLPT: new method of removing ghost particles and high-concentration particle shadow tracking. Exp. Fluids 61 (2), 47.CrossRefGoogle Scholar
Verschoof, R.A., Van Der Veen, R.C.A., Sun, C. & Lohse, D. 2016 Bubble drag reduction requires large bubbles. Phys. Rev. Lett. 117 (10), 104502.CrossRefGoogle ScholarPubMed
Volk, R., Calzavarini, E., Leveque, E. & Pinton, J.-F. 2011 Dynamics of inertial particles in a turbulent von Kármán flow. J. Fluid Mech. 668, 223–235.CrossRefGoogle Scholar
Volk, R., Calzavarini, E., Verhille, G., Lohse, D., Mordant, N., Pinton, J.-F. & Toschi, F. 2008 Acceleration of heavy and light particles in turbulence: comparison between experiments and direct numerical simulations. Physica D 237 (14–17), 2084–2089.CrossRefGoogle Scholar
Voth, G.A. 2000 Lagrangian Acceleration Measurements in Turbulence at Large Reynolds Numbers. Cornell University.Google Scholar
Voth, G.A., La Porta, A., Crawford, A.M., Alexander, J. & Bodenschatz, E. 2002 Measurement of particle accelerations in fully developed turbulence. J. Fluid Mech. 469, 121–160.CrossRefGoogle Scholar
Yu, X., Hendrickson, K. & Yue, D.K.P. 2020 Scale separation and dependence of entrainment bubble-size distribution in free-surface turbulence. J. Fluid Mech. 885, R2.CrossRefGoogle Scholar