Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Wang, W. B.
Hu, R. F.
Xu, S. J.
and
Wu, Z. N.
2013.
Influence of aspect ratio on tumbling plates.
Journal of Fluid Mechanics,
Vol. 733,
Issue. ,
p.
650.
Lee, Cunbiao
Su, Zhuang
Zhong, Hongjie
Chen, Shiyi
Zhou, Mingde
and
Wu, Jiezhi
2013.
Experimental investigation of freely falling thin disks. Part 2. Transition of three-dimensional motion from zigzag to spiral.
Journal of Fluid Mechanics,
Vol. 732,
Issue. ,
p.
77.
Zhu, Yiding
Yuan, Huijing
Zhang, Chuanhong
and
Lee, Cunbiao
2013.
Image-preprocessing method for near-wall particle image velocimetry (PIV) image interrogation with very large in-plane displacement.
Measurement Science and Technology,
Vol. 24,
Issue. 12,
p.
125302.
Hu, Ruifeng
and
Wang, Lifeng
2014.
Motion transitions of falling plates via quasisteady aerodynamics.
Physical Review E,
Vol. 90,
Issue. 1,
Wang, Jiao
Liu, Caishan
and
Ma, Daolin
2014.
Experimental study of transport of a dimer on a vertically oscillating plate.
Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 470,
Issue. 2171,
p.
20140439.
Ma, Daolin
Liu, Caishan
Zhao, Zhen
and
Zhang, Hongjian
2014.
Rolling friction and energy dissipation in a spinning disc.
Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 470,
Issue. 2169,
p.
20140191.
Rahmani, M.
and
Wachs, A.
2014.
Free falling and rising of spherical and angular particles.
Physics of Fluids,
Vol. 26,
Issue. 8,
Quan, Chenggen
Qian, Kemao
Asundi, Anand
Chau, Fook Siong
Lyu, Xujian
Wei, Zhaoyu
Tang, Hui
New, T. H.
and
Li, Hua
2015.
On the motion of a falling circular cylinder in flows after water entry.
Vol. 9302,
Issue. ,
p.
930233.
Zhu Pan-Cheng
Bian Qing-Yong
and
Li Jin-Bin
2015.
Relations among different energy dissipations of Euler disk.
Acta Physica Sinica,
Vol. 64,
Issue. 17,
p.
174501.
Hamed, Ali M.
Jin, Yaqing
and
Chamorro, Leonardo P.
2015.
On the transient dynamics of the wake and trajectory of free falling cones with various apex angles.
Experiments in Fluids,
Vol. 56,
Issue. 11,
Zhang, Chuanhong
Zhu, Yiding
Chen, Xi
Yuan, Huijing
Wu, Jiezhi
Chen, Shiyi
Lee, Cunbiao
and
Gad-el-Hak, Mohamed
2015.
Transition in hypersonic boundary layers.
AIP Advances,
Vol. 5,
Issue. 10,
Wang, Y.
Shu, C.
Teo, C. J.
and
Yang, L. M.
2016.
Numerical study on the freely falling plate: Effects of density ratio and thickness-to-length ratio.
Physics of Fluids,
Vol. 28,
Issue. 10,
Wang, Y.
Shu, C.
Teo, C.J.
and
Yang, L.M.
2016.
An efficient immersed boundary-lattice Boltzmann flux solver for simulation of 3D incompressible flows with complex geometry.
Computers & Fluids,
Vol. 124,
Issue. ,
p.
54.
Ma, Daolin
and
Liu, Caishan
2016.
Dynamics of a Spinning Disk.
Journal of Applied Mechanics,
Vol. 83,
Issue. 6,
Zhu, Yiding
Zhang, Chuanhong
Chen, Xi
Yuan, Huijing
Wu, Jiezhi
Chen, Shiyi
Lee, Cunbiao
and
Gad-el-Hak, Mohamed
2016.
Transition in Hypersonic Boundary Layers: Role of Dilatational Waves.
AIAA Journal,
Vol. 54,
Issue. 10,
p.
3039.
Bai Ye
Jia Yong-Xia
Li Cun-Biao
and
Zhu Yi-Ding
2016.
Experimental Study of a Periodical Flapping Flag.
Acta Physica Sinica,
Vol. 65,
Issue. 12,
p.
124701.
Wang, Jiao
Liu, Caishan
Wiercigroch, Marian
Wang, Chenghua
and
Shui, Yongtao
2016.
Stability of periodic modes and bifurcation behaviors in a bouncing-dimer system.
Nonlinear Dynamics,
Vol. 86,
Issue. 3,
p.
1477.
Wang, Y.
Shu, C.
Yang, L.M.
and
Teo, C.J.
2017.
An immersed boundary-lattice boltzmann flux solver in a moving frame to study three-dimensional freely falling rigid bodies.
Journal of Fluids and Structures,
Vol. 68,
Issue. ,
p.
444.
Sun, Y.
Shu, C.
Wang, Y.
Teo, C.J.
and
Chen, Z.
2017.
An immersed boundary-gas kinetic flux solver for simulation of incompressible flows
.
Computers & Fluids,
Vol. 142,
Issue. ,
p.
45.
He, Zhiwei
Tian, Baolin
Zhang, Yousheng
and
Gao, Fujie
2017.
Characteristic-based and interface-sharpening algorithm for high-order simulations of immiscible compressible multi-material flows.
Journal of Computational Physics,
Vol. 333,
Issue. ,
p.
247.
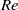 $\mathit{Re}$. At high Reynolds numbers a new dipole vortex is shed that is significantly different from Kármán-type vortices. The vortical structures are mainly composed of leading-edge vortices, a counter-rotating vortex pair and secondary trailing-edge vortices. The amplitude of the horizontal oscillation is also dependent on the Reynolds number with a critical Reynolds number
$\mathit{Re}$. At high Reynolds numbers a new dipole vortex is shed that is significantly different from Kármán-type vortices. The vortical structures are mainly composed of leading-edge vortices, a counter-rotating vortex pair and secondary trailing-edge vortices. The amplitude of the horizontal oscillation is also dependent on the Reynolds number with a critical Reynolds number  ${\mathit{Re}}_{cr} \approx 2000$, where the oscillatory amplitude is proportional to
${\mathit{Re}}_{cr} \approx 2000$, where the oscillatory amplitude is proportional to 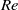 $\mathit{Re}$ for
$\mathit{Re}$ for 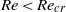 $\mathit{Re}\lt {\mathit{Re}}_{cr} $, but becomes invariant for
$\mathit{Re}\lt {\mathit{Re}}_{cr} $, but becomes invariant for 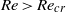 $\mathit{Re}\gt {\mathit{Re}}_{cr} $. Three-dimensional dipolar vortices were also observed experimentally.
$\mathit{Re}\gt {\mathit{Re}}_{cr} $. Three-dimensional dipolar vortices were also observed experimentally.

