Hostname: page-component-848d4c4894-5nwft Total loading time: 0 Render date: 2024-05-13T18:45:44.863Z Has data issue: false hasContentIssue false
  • English
  • Français

Exact coherent states of attached eddies in channel flow

Published online by Cambridge University Press:  16 January 2019

Qiang Yang ,
Ashley P. Willis Open the ORCID record for Ashley P. Willis [Opens in a new window]  and
Yongyun Hwang Open the ORCID record for Yongyun Hwang [Opens in a new window]
Qiang Yang
Affiliation:
State Key Laboratory of Aerodynamics, China Aerodynamics Research and Development Centre, Mianyang621000, PR China Department of Aeronautics, Imperial College London, South Kensington, London SW7 2AZ, UK
Ashley P. Willis
Affiliation:
School of Mathematics and Statistics, University of Sheffield, Sheffield S3 7RH, UK
Yongyun Hwang*
Affiliation:
Department of Aeronautics, Imperial College London, South Kensington, London SW7 2AZ, UK
*
†Email address for correspondence: y.hwang@imperial.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

A new set of exact coherent states in the form of a travelling wave is reported in plane channel flow. They are continued over a range in 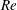$Re$ from approximately 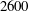$2600$ up to 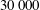$30\,000$, an order of magnitude higher than those discovered in the transitional regime. This particular type of exact coherent states is found to be gradually more localised in the near-wall region on increasing the Reynolds number. As larger spanwise sizes 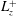$L_{z}^{+}$ are considered, these exact coherent states appear via a saddle-node bifurcation with a spanwise size of 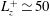$L_{z}^{+}\simeq 50$ and their phase speed is found to be 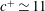$c^{+}\simeq 11$ at all the Reynolds numbers considered. Computation of the eigenspectra shows that the time scale of the exact coherent states is given by 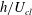$h/U_{cl}$ in channel flow at all Reynolds numbers, and it becomes equivalent to the viscous inner time scale for the exact coherent states in the limit of 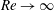$Re\rightarrow \infty$. The exact coherent states at several different spanwise sizes are further continued to a higher Reynolds number, 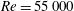$Re=55\,000$, using the eddy-viscosity approach (Hwang & Cossu, Phys. Rev. Lett., vol. 105, 2010, 044505). It is found that the continued exact coherent states at different sizes are self-similar at the given Reynolds number. These observations suggest that, on increasing Reynolds number, new sets of self-sustaining coherent structures are born in the near-wall region. Near this onset, these structures scale in inner units, forming the near-wall self-sustaining structures. With further increase of Reynolds number, the structures that emerged at lower Reynolds numbers subsequently evolve into the self-sustaining structures in the logarithmic region at different length scales, forming a hierarchy of self-similar coherent structures as hypothesised by Townsend (i.e. attached eddy hypothesis). Finally, the energetics of turbulent flow is discussed for a consistent extension of these dynamical systems notions to high Reynolds numbers.

JFM classification

Turbulent Flows: Turbulent boundary layers Turbulent Flows: Turbulence theory
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 862 , 10 March 2019 , pp. 1029 - 1059
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Afzal, N. 1982 Fully developed turbulent flow in a pipe: an intermediate layer. Ing.-Arch. 52, 355–377.10.1007/BF00536208Google Scholar
del Álamo, J. C. & Jiménez, J. 2003 Spectra of the very large anisotropic scales in turbulent channels. Phys. Fluids 15, L41.Google Scholar
del Álamo, J. C. & Jiménez, J. 2006 Linear energy amplification in turbulent channels. J. Fluid Mech. 559, 205–213.Google Scholar
del Álamo, J. C., Jiménez, J., Zandonade, P. & Moser, R. D. 2006 Self-similar vortex clusters in the turbulent logarithmic region. J. Fluid Mech. 561, 329–358.Google Scholar
Alizard, F. 2015 Linear stability of optimal streaks in the log-layer of turbulent channel flows. Phys. Fluids 27, 105103.Google Scholar
Bewley, T. R. 2014 Numerical Renaissance: Simulation, Optimization, and Control. Renaissance Press.Google Scholar
Budanur, N. B. & Hof, B. 2017 Heteroclinic path to spatially localized chaos in pipe flow. J. Fluid Mech. 827, R1.Google Scholar
Butler, K. M. & Farrell, B. F. 1993 Optimal perturbations and streak spacing in wall-bounded turbulent shear flow. Phys. Fluids 5, 774–777.Google Scholar
Cassinelli, A., de Giovanetti, M. & Hwang, Y. 2017 Streak instability in near-wall turbulence revisited. J. Turbul. 18 (5), 443–464.Google Scholar
Chini, G. P., Montemuro, B., White, C. M. & Klewicki, J. 2017 A self-sustaining process model of inertial layer dynamics in high Reynolds number turbulent wall flows. Phil. Trans. R. Soc. Lond. 95, 264504.Google Scholar
Cho, M., Hwang, Y. & Choi, H. 2018 Scale interactions and spectral energy transfer in turbulent channel flow. J. Fluid Mech. 854, 474–504.10.1017/jfm.2018.643Google Scholar
Cossu, C., Pujals, G. & Depardon, S. 2009 Optimal transient growth and very large scale structures in turbulent boundary layers. J. Fluid Mech. 619, 79–94.10.1017/S0022112008004370Google Scholar
Deguchi, K. 2015 Self-sustaining states at Kolmogorov microscale. J. Fluid Mech. 781, R6.Google Scholar
Eckhardt, B. & Zammert, S. 2018 Small scale exact coherent structures at large Reynolds numbers in plane Couette flow. Nonlinearity 31, R66–R77.Google Scholar
Faisst, H. & Eckhardt, B. 2004 Sensitive dependence on initial conditions in transition to turbulence. J. Fluid Mech. 504, 343–352.Google Scholar
Fukagata, K., Iwamoto, K. & Kasagi, N. 2002 Contribution of Reynolds stress distribution to the skin friction in wall-bounded flows. Phys. Fluids 14 (11), 13–17.Google Scholar
Gibson, J. F., Halcrow, J. & Cvitanovic, P. 2008 Visualizing the geometry of state space in plane Couette flow. J. Fluid Mech. 611, 107–130.Google Scholar
Gibson, J. F., Halcrow, J. & Cvitanovic, P. 2009 Equilibrium and traveling-wave solutions of plane Couette flow. J. Fluid Mech. 638, 243–266.Google Scholar
de Giovanetti, M., Hwang, Y. & Choi, H. 2016 Skin-friction generation by attached eddies in turbulent channel flow. J. Fluid Mech. 808, 511–538.Google Scholar
de Giovanetti, M., Sung, H. J. & Hwang, Y. 2017 Streak instability in turbulent channel flow: the seeding mechanism of large-scale motions. J. Fluid Mech. 832, 483–513.Google Scholar
Hamilton, J. M., Kim, J. & Waleffe, F. 1995 Regeneration mechanisms of near-wall turbulence structures. J. Fluid Mech. 287, 317–348.Google Scholar
Head, M. R. & Bandyopadhay, P. 1981 New aspects of turbulent boundary-layer structure. J. Fluid Mech. 107, 297–338.Google Scholar
Hellstöm, L. H. O., Marusic, I. & Smits, A. J. 2016 Self-similarity of the large-scale motions in turbulent pipe flow. J. Fluid Mech. 792, R1.10.1017/jfm.2016.100Google Scholar
Hutchins, N. & Marusic, I. 2007 Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 1–28.Google Scholar
Hwang, Y. 2013 Near-wall turbulent fluctuations in the absence of wide outer motions. J. Fluid Mech. 723, 264–288.Google Scholar
Hwang, Y. 2015 Statistical structure of self-sustaining attached eddies in turbulent channel flow. J. Fluid Mech. 723, 264–288.Google Scholar
Hwang, Y. & Bengana, Y. 2016 Self-sustaining process of minimal attached eddies in turbulent channel flow. J. Fluid Mech. 795, 708–738.Google Scholar
Hwang, Y. & Cossu, C. 2010a Linear non-normal energy amplification of harmonic and stochastic forcing in the turbulent channel flow. J. Fluid Mech. 664, 51–73.Google Scholar
Hwang, Y. & Cossu, C. 2010b Self-sustained process at large scales in turbulent channel flow. Phys. Rev. Lett. 105, 044505.Google Scholar
Hwang, Y. & Cossu, C. 2011 Self-sustained processes in the logarithmic layer of turbulent channel flows. Phys. Fluid 23, 061702.10.1063/1.3599157Google Scholar
Hwang, Y., Willis, A. P. & Cossu, C. 2016 Invariant solutions of minimal large-scale structures in turbulent channel flow for Re 𝜏 up to 1000. J. Fluid Mech. 802, R1.Google Scholar
Jeong, J., Benney, F., Schoppa, W. & Kim, J. 1997 Coherent structures near the wall in a turbulent channel flow. J. Fluid Mech. 332, 185–214.Google Scholar
Jeong, J. & Hussain, F. 1995 On the identification of a vortex. J. Fluid Mech. 285, 69–94.Google Scholar
Jiménez, J. & Pinelli, A. 1999 The autonomous cycle of near-wall turbulence. J. Fluid Mech. 389, 335–359.Google Scholar
Jiménez, J. & Simens, M. P. 2001 Low-dimensional dynamics of a turbulent wall flow. J. Fluid Mech. 435, 81–91.Google Scholar
von Kármán, T. 1930 Mechanische aehnlichkeit und turbulenz. Nachr. Ges. Wiss. Göttingen, Math. Phys. Kl. 58–68; English translation NACA TM 611.Google Scholar
Kawahara, G. & Kida, S. 2001 Periodic motion embedded in plane Couette turbulence: regeneration cycle and burst. J. Fluid Mech. 449, 291–300.Google Scholar
Kim, J. & Hussain, F. 1993 Propagation velocity of perturbations in turbulent channel flow. Phys. Fluids 5, 695–706.10.1063/1.858653Google Scholar
Kim, K. C. & Adrian, R. 1999 Very large-scale motion in the outer layer. Phys. Fluids 11 (2), 417–422.Google Scholar
Kline, S. J., Reynolds, W. C., Schraub, F. A. & Runstadler, P. W. 1967 The structure of turbulent boundary layers. J. Fluid Mech. 30, 741–773.Google Scholar
Kovasznay, L. S. G., Kibens, V. & Blackwelder, R. F. 1970 Large-scale motion in the intermittent region of a turbulent boundary layer. J. Fluid Mech. 41, 283–325.Google Scholar
Lee, M. & Moser, R. D. 2019 Spectral analysis of the budget equation in turbulent channel flows at high Reynolds number. J. Fluid Mech. 860, 886–938.Google Scholar
Marusic, I. & Monty, J. P. 2019 Attached eddy model of wall turbulence. Annu. Rev. Fluid Mech. 51, 49–74.Google Scholar
Marusic, I., Monty, J. P., Hultmark, M. & Smits, A. J. 2013 On the logarithmic region in wall turbulence. J. Fluid Mech. 716, R3.Google Scholar
McKeon, B. J. & Sharma, A. S. 2010 A critical-layer framework for turbulent pipe flow. J. Fluid Mech. 658, 336–382.Google Scholar
Mellibovsky, F. & Eckhardt, B. 2011 Takens–Bogdanov bifurcation of travelling-wave solutions in pipe flow. J. Fluid Mech. 670, 96–129.Google Scholar
Moarref, R., Sharma, A. S., Tropp, J. A. & McKeon, B. J. 2013 Model-based scaling of the streamwise energy density in high-Reynolds-number turbulent channels. J. Fluid Mech. 734, 275–316.Google Scholar
Moser, R. D., Kim, J. & Mansour, N. N. 1999 Direct numerical simulation of turbulent channel flow up to Re = 590. Phys. Fluids 11, 943–945.Google Scholar
Nagata, M. 1990 Three-dimensional finite-amplitude solutions in plane Couette flow: bifurcation from infinity. J. Fluid Mech. 217, 519–527.Google Scholar
Neelavara, S. A., Duguet, Y. & Lusseyran, F. 2017 State space analysis of minimal channel flow. Fluid Dyn. Res. 49, 035511.Google Scholar
Park, J., Hwang, Y. & Cossu, C. 2011 On the stability of large-scale streaks in the turbulent Couette and Poiseuille flows. C. R. Méc. 339 (1), 1–5.Google Scholar
Perry, A. E. & Chong, M. S. 1982 On the mechanism of turbulence. J. Fluid Mech. 119, 173–217.Google Scholar
Perry, A. E., Henbest, S. & Chong, M. S. 1986 A theoretical and experimental study of wall turbulence. J. Fluid Mech. 165, 163–199.10.1017/S002211208600304XGoogle Scholar
Perry, A. E. & Marusic, I. 1995 A wall-wake model for the turbulence structure of boundary layers. Part 1. Extension of the attached eddy hypothesis. J. Fluid Mech. 298, 361–388.Google Scholar
Prandtl, L. 1925 Bericht über doe emtstejimg der turbulenz. Z. Angew. Math. Mech. 5, 136–139.Google Scholar
Pujals, G., García-Villalba, M., Cossu, C. & Depardon, S. 2009 A note on optimal transient growth in turbulent channel flows. Phys. Fluids 21, 015109.Google Scholar
Rawat, S., Cossu, C., Hwang, Y. & Rincon, F. 2015 On the self-sustained nature of large-scale motions in turbulent Couette flow. J. Fluid Mech. 782, 515–540.10.1017/jfm.2015.550Google Scholar
Rawat, S., Cossu, C. & Rincon, F. 2016 Travelling-wave solutions bifurcating from relative periodic orbits in plane Poiseuille flow. C. R. Méc. 344, 448–455.Google Scholar
Schoppa, W. & Hussain, F. 2002 Coherent structure generation in near-wall turbulence. J. Fluid Mech. 453, 57–108.Google Scholar
Smagorinsky, J. 1963 General circulation experiments with the primitive equations: I. The basic equations. Mon. Weath. Rev. 91, 99–164.Google Scholar
Sreenivasan, K. R. & Sahay, A. 1997 The persistence of viscous effects in the overlap region and the mean velocity in turbulent pipe and channel flows. In Self-Sustaining Mechanisms of Wall Turbulence (ed. Panton, R.), pp. 253–272. Computational Mechanics.Google Scholar
Tennekes, H. & Lumley, J. L. 1967 A First Course in Turbulence. MIT Press.Google Scholar
Townsend, A. A. 1956 The Structure of Turbulent Shear Flow, 1st edn. Cambridge University Press.Google Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flow, 2nd edn. Cambridge University Press.Google Scholar
Viswanath, D. 2007 Recurrent motions within plane Couette turbulence. J. Fluid Mech. 580, 339–358.Google Scholar
Waleffe, F. 1997 On a self-sustaining process in shear flows. Phys. Fluids 9, 883–900.Google Scholar
Waleffe, F. 1998 Three-dimensional coherent states in plane shear flows. Phys. Rev. Lett. 81, 4140–4143.10.1103/PhysRevLett.81.4140Google Scholar
Waleffe, F. 2001 Exact coherent structures in channel flow. J. Fluid Mech. 435, 93–102.Google Scholar
Waleffe, F. 2003 Homotopy of exact coherent structures in plane shear flows. Phys. Fluids 15, 1517–1534.Google Scholar
Wedin, H. & Kerswell, R. R. 2004 Exact coherent structures in pipe flow: travelling wave solutions. J. Fluid Mech. 508, 333–371.Google Scholar
Willis, A. P., Cvitanovic, P. & Avila, M. 2013 Revealing the state space of turbulent pipe flow by symmetry reduction. J. Fluid Mech. 721, 514–540.10.1017/jfm.2013.75Google Scholar
Willis, A. P., Cvitanovic, P. & Avila, M. 2016 Symmetry reduction in high dimensions, illustrated in a turbulent pipe. Phys. Rev. E 93, 022204.Google Scholar
Willis, A. P., Hwang, Y. & Cossu, C. 2010 Optimally amplified large-scale streaks and drag reduction in the turbulent pipe flow. Phys. Rev. E 82, 036321.Google Scholar
Woodcock, J. D. & Marusic, I. 2015 The statistics behaviour of attached eddies. Phys. Fluids 27, 015104.10.1063/1.4905301Google Scholar
Yang, Q., Willis, A. P. & Hwang, Y. 2018 Energy production and self-sustained turbulence at the Kolmogorov scale in Couette flow. J. Fluid Mech. 834, 531–554.Google Scholar