Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-21T16:08:14.540Z Has data issue: false hasContentIssue false
  • English
  • Français

Evolution of similarity lengths in anisotropic magnetohydrodynamic turbulence

Published online by Cambridge University Press:  31 July 2019

Riddhi Bandyopadhyay Open the ORCID record for Riddhi Bandyopadhyay [Opens in a new window] ,
William H. Matthaeus Open the ORCID record for William H. Matthaeus [Opens in a new window] ,
Sean Oughton Open the ORCID record for Sean Oughton [Opens in a new window]  and
Minping Wan Open the ORCID record for Minping Wan [Opens in a new window]
Riddhi Bandyopadhyay
Affiliation:
Department of Physics and Astronomy, University of Delaware, Newark, DE 19716, USA Bartol Research Institute, University of Delaware, Newark, DE 19716, USA
William H. Matthaeus*
Affiliation:
Department of Physics and Astronomy, University of Delaware, Newark, DE 19716, USA Bartol Research Institute, University of Delaware, Newark, DE 19716, USA
Sean Oughton
Affiliation:
Department of Mathematics and Statistics, University of Waikato, Hamilton 3240, NZ
Minping Wan
Affiliation:
Department of Mechanics and Aerospace Engineering, Southern University of Science and Technology, Shenzhen, Guangdong 518055, PR China
*
†Email address for correspondence: whm@udel.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

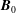In an earlier paper (Wan et al., J. Fluid Mech., vol. 697, 2012, pp. 296–315), the authors showed that a similarity solution for anisotropic incompressible three-dimensional magnetohydrodynamic (MHD) turbulence, in the presence of a uniform mean magnetic field $\boldsymbol{B}_{0}$, exists if the ratio of parallel to perpendicular (with respect to 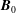$\boldsymbol{B}_{0}$) similarity length scales remains constant in time. This conjecture appears to be a rather stringent constraint on the dynamics of decay of the energy-containing eddies in MHD turbulence. However, we show here, using direct numerical simulations, that this hypothesis is indeed satisfied in incompressible MHD turbulence. After an initial transient period, the ratio of parallel to perpendicular length scales fluctuates around a steady value during the decay of the eddies. We show further that a Taylor–Kármán-like similarity decay holds for MHD turbulence in the presence of a mean magnetic field. The effect of different parameters, including Reynolds number, mean field strength, and cross-helicity, on the nature of similarity decay is discussed.

JFM classification

Turbulent Flows: Homogeneous turbulence MHD and Electrohydrodynamics: MHD turbulence Turbulent Flows: Turbulence theory
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 876 , 10 October 2019 , pp. 5 - 18
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bandyopadhyay, R., Chasapis, A., Chhiber, R., Parashar, T. N., Matthaeus, W. H., Shay, M. A., Maruca, B. A., Burch, J. L., Moore, T. E., Pollock, C. J. et al. 2018 Incompressive energy transfer in the earth’s magnetosheath: magnetospheric multiscale observations. Astrophys. J. 866 (2), 106.Google Scholar
Bandyopadhyay, R., Oughton, S., Wan, M., Matthaeus, W. H., Chhiber, R. & Parashar, T. N. 2018b Finite dissipation in anisotropic magnetohydrodynamic turbulence. Phys. Rev. X 8, 041052.Google Scholar
Batchelor, G. K. 1953 The Theory of Homogeneous Turbulence. Cambridge University Press.Google Scholar
Bigot, B., Galtier, S. & Politano, H. 2008a Development of anisotropy in incompressible magnetohydrodynamic turbulence. Phys. Rev. E 78, 066301.Google Scholar
Bigot, B., Galtier, S. & Politano, H. 2008b Energy decay laws in strongly anisotropic magnetohydrodynamic turbulence. Phys. Rev. Lett. 100, 074502.Google Scholar
Biskamp, D. & Schwarz, E. 2001 On two-dimensional magnetohydrodynamic turbulence. Phys. Plasmas 8 (7), 3282–3292.Google Scholar
Breech, B., Matthaeus, W. H., Minnie, J., Bieber, J. W., Oughton, S., Smith, C. W. & Isenberg, P. A. 2008 Turbulence transport throughout the heliosphere. J. Geophys. Res. 113 (A8), A08105.Google Scholar
Dobrowolny, M., Mangeney, A. & Veltri, P. 1980 Fully developed anisotropic hydromagnetic turbulence in interplanetary space. Phys. Rev. Lett. 45, 144–147.Google Scholar
Donzis, D. A., Yeung, P. K. & Sreenivasan, K. R. 2008 Dissipation and enstrophy in isotropic turbulence: resolution effects and scaling in direct numerical simulations. Phys. Fluids 20, 045108.Google Scholar
Dryden, H. L. 1943 A review of the statistical theory of turbulence. Q. Appl. Maths 1 (1), 7–42.Google Scholar
Ghosh, S., Matthaeus, W. H. & Montgomery, D. 1988 The evolution of cross-helicity in driven/dissipative two-dimensional magnetohydrodynamics. Phys. Fluids 31 (8), 2171–2184.Google Scholar
Goldreich, P. & Sridhar, S. 1995 Toward a theory of interstellar turbulence: II. Strong Alfvénic turbulence. Astrophys. J. 438, 763–775.Google Scholar
Grappin, R. 1986 Onset and decay of two-dimensional magnetohydrodynamic turbulence with velocity–magnetic field correlation. Phys. Fluids 29, 2433–2443.Google Scholar
Hossain, M., Gray, P. C., Pontius, D. H. Jr., Matthaeus, W. H. & Oughton, S. 1995 Phenomenology for the decay of energy-containing eddies in homogeneous MHD turbulence. Phys. Fluids 7 (11), 2886–2904.Google Scholar
Hossain, M., Gray, P. C., Pontius, D. H. Jr., Matthaeus, W. H. & Oughton, S. 1996 Is the Alfvén-wave propagation effect important for energy decay in homogeneous MHD turbulence? AIP Conf. Proc. 382 (1), 358–361.Google Scholar
de Kármán, T. & Howarth, L. 1938 On the statistical theory of isotropic turbulence. Proc. R. Soc. Lond. A 164, 192–215.Google Scholar
von Kármán, T. & Lin, C. C. 1949 On the concept of similarity in the theory of isotropic turbulence. Rev. Mod. Phys. 21, 516–519.Google Scholar
Kolmogorov, A. N. 1941 Dissipation of energy in the locally isotropic turbulence. C. R. Acad. Sci. URSS 32, 16 (Reprinted in Proc. R. Soc. Lond. A 434, 15–17 (1991)).Google Scholar
Linkmann, M., Berera, A. & Goldstraw, E. E. 2017 Reynolds-number dependence of the dimensionless dissipation rate in homogeneous magnetohydrodynamic turbulence. Phys. Rev. E 95, 013102.Google Scholar
Linkmann, M. F., Berera, A., McComb, W. D. & McKay, M. E. 2015 Nonuniversality and finite dissipation in decaying magnetohydrodynamic turbulence. Phys. Rev. Lett. 114, 235001.Google Scholar
Matthaeus, W. H., Goldstein, M. L. & Montgomery, D. C. 1983 Turbulent generation of outward-traveling interplanetary Alfvénic fluctuations. Phys. Rev. Lett. 51, 1484–1487.Google Scholar
Matthaeus, W. H., Goldstein, M. L. & Roberts, D. A. 1990 Evidence for the presence of quasi-two-dimensional nearly incompressible fluctuations in the solar wind. J. Geophys. Res. 95 (A12), 20673–20683.Google Scholar
Matthaeus, W. H., Zank, G. P. & Oughton, S. 1996 Phenomenology of hydromagnetic turbulence in a uniformly expanding medium. J. Plasma Phys. 56 (3), 659–675.Google Scholar
Monin, A. S. & Yaglom, A. M. 1975 Statistical Fluid Mechanics, vol. 2. MIT Press.Google Scholar
Montgomery, D. C. 1982 Major disruption, inverse cascades, and the Strauss equations. Phys. Scr. T2/1, 83–88.Google Scholar
Montgomery, D. C. & Turner, L. 1981 Anisotropic magnetohydrodynamic turbulence in a strong external magnetic field. Phys. Fluids 24, 825–831.Google Scholar
Onsager, L. 1949 Statistical hydrodynamics. Il Nuovo Cimento 6, 279–287.Google Scholar
Oughton, S., Dmitruk, P. & Matthaeus, W. H. 2004 Reduced magnetohydrodynamics and parallel spectral transfer. Phys. Plasmas 11 (5), 2214–2225.Google Scholar
Oughton, S. & Matthaeus, W. H. 2005 Parallel and perpendicular cascades in solar wind turbulence. Nonlinear Process. Geophys. 12 (2), 299–310.Google Scholar
Oughton, S., Matthaeus, W. H., Smith, C. W., Breech, B. & Isenberg, P. A. 2011 Transport of solar wind fluctuations: a two-component model. J. Geophys. Res. 116, A08105.Google Scholar
Oughton, S., Priest, E. R. & Matthaeus, W. H. 1994 The influence of a mean magnetic field on three-dimensional magnetohydrodynamic turbulence. J. Fluid Mech. 280, 95–117.Google Scholar
Oughton, S., Wan, M., Servidio, S. & Matthaeus, W. H. 2013 On the origin of anisotropy in magnetohydrodynamic turbulence: the role of higher-order correlations. Astrophys. J. 768, 10.Google Scholar
Parashar, T. N., Matthaeus, W. H., Shay, M. A. & Wan, M. 2015 Transition from kinetic to MHD behavior in a collisionless plasma. Astrophys. J. 811 (2), 112.Google Scholar
Politano, H., Gomez, T. & Pouquet, A. 2003 von Kármán–Howarth relationship for helical magnetohydrodynamic flows. Phys. Rev. E 68, 026315.Google Scholar
Politano, H. & Pouquet, A. 1998a Dynamical length scales for turbulent magnetized flows. Geophys. Res. Lett. 25 (3), 273–276.Google Scholar
Politano, H. & Pouquet, A. 1998b von Kármán–Howarth equation for magnetohydrodynamics and its consequences on third-order longitudinal structure and correlation functions. Phys. Rev. E 57, R21–R24.Google Scholar
Robinson, D. C. & Rusbridge, M. G. 1971 Structure of turbulence in the zeta plasma. Phys. Fluids 14, 2499–2511.Google Scholar
Shebalin, J. V., Matthaeus, W. H. & Montgomery, D. 1983 Anisotropy in MHD turbulence due to a mean magnetic field. J. Plasma Phys. 29 (3), 525–547.Google Scholar
Taylor, G. I. 1938 The spectrum of turbulence. Proc. R. Soc. Lond. A 164, 476–490.Google Scholar
Teaca, B., Verma, M. K., Knaepen, B. & Carati, D. 2009 Energy transfer in anisotropic magnetohydrodynamic turbulence. Phys. Rev. E 79, 046312.Google Scholar
Usmanov, A. V., Goldstein, M. L. & Matthaeus, W. H. 2014 Three-fluid, three-dimensional magnetohydrodynamic solar wind model with eddy viscosity and turbulent resistivity. Astrophys. J. 788 (1), 43.Google Scholar
Verma, M. K. 2017 Anisotropy in quasi-static magnetohydrodynamic turbulence. Rep. Prog. Phys. 80 (8), 087001.Google Scholar
Wan, M., Oughton, S., Servidio, S. & Matthaeus, W. H. 2010 On the accuracy of simulations of turbulence. Phys. Plasmas 17 (8), 082308.Google Scholar
Wan, M., Oughton, S., Servidio, S. & Matthaeus, W. H. 2012 von Kármán self-preservation hypothesis for magnetohydrodynamic turbulence and its consequences for universality. J. Fluid Mech. 697, 296–315.Google Scholar
Wu, P., Wan, M., Matthaeus, W. H., Shay, M. A. & Swisdak, M. 2013 von Kármán energy decay and heating of protons and electrons in a kinetic turbulent plasma. Phys. Rev. Lett. 111, 121105.Google Scholar
Zank, G. P., Matthaeus, W. H. & Smith, C. W. 1996 Evolution of turbulent magnetic fluctuation power with heliocentric distance. J. Geophys. Res. 101, 17093–17107.Google Scholar