Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Choudhary, Akash
Renganathan, T.
and
Pushpavanam, S.
2020.
Non-Newtonian effects on the slip and mobility of a self-propelling active particle.
Journal of Fluid Mechanics,
Vol. 899,
Issue. ,
Li, Gaojin
Lauga, Eric
and
Ardekani, Arezoo M.
2021.
Microswimming in viscoelastic fluids.
Journal of Non-Newtonian Fluid Mechanics,
Vol. 297,
Issue. ,
p.
104655.
Bharti
Gopmandal, Partha P.
Bhattacharyya, S.
and
Ohshima, H.
2021.
A simplified model for gel electrophoresis of a hydrophobic rigid colloid.
Soft Matter,
Vol. 17,
Issue. 23,
p.
5700.
Ghosh, Uddipta
Mukherjee, Siddhartha
and
Chakraborty, Suman
2021.
Electrophoretic motion of a non-uniformly charged particle in a viscoelastic medium in thin electrical double layer limit.
Journal of Fluid Mechanics,
Vol. 924,
Issue. ,
Bentor, Joseph
Malekanfard, Amirreza
Raihan, Mahmud Kamal
Wu, Sen
Pan, Xinxiang
Song, Yongxin
and
Xuan, Xiangchun
2021.
Insulator‐based dielectrophoretic focusing and trapping of particles in non‐Newtonian fluids.
ELECTROPHORESIS,
Vol. 42,
Issue. 21-22,
p.
2154.
Natu, Aditya
and
Ghosh, Uddipta
2021.
Electrokinetics of polymeric fluids in narrow rectangular confinements.
Soft Matter,
Vol. 17,
Issue. 38,
p.
8712.
Xuan, Xiangchun
2022.
Review of nonlinear electrokinetic flows in insulator‐based dielectrophoresis: From induced charge to Joule heating effects.
ELECTROPHORESIS,
Vol. 43,
Issue. 1-2,
p.
167.
Bentor, Joseph
Raihan, Mahmud Kamal
McNeely, Colin
Liu, Zhijian
Song, Yongxin
and
Xuan, Xiangchun
2022.
Fluid rheological effects on streaming dielectrophoresis in a post‐array microchannel.
ELECTROPHORESIS,
Vol. 43,
Issue. 5-6,
p.
717.
Chang, Hui
Li, Deyu
Zhang, Xiangyu
Xu, Runxin
Zhang, Junyan
and
Song, Yongxin
2022.
Size‐dependent electrophoretic motion of polystyrene particles at polyethylene glycol–dextran interfaces.
ELECTROPHORESIS,
Vol. 43,
Issue. 21-22,
p.
2112.
Bharti
Sarkar, Sankar
Ohshima, H.
and
Gopmandal, Partha P.
2022.
Gel Electrophoresis of a Hydrophobic Liquid Droplet with an Equipotential Slip Surface.
Langmuir,
Vol. 38,
Issue. 29,
p.
8943.
Kouni, Eleni
Moschopoulos, Pantelis
Dimakopoulos, Yannis
and
Tsamopoulos, John
2023.
Sedimentation of a Charged Spherical Particle in a Viscoelastic Electrolyte Solution.
Langmuir,
Vol. 39,
Issue. 45,
p.
16006.
Li, Gaojin
2023.
Slow motion of a sphere near a sinusoidal surface.
Journal of Fluid Mechanics,
Vol. 975,
Issue. ,
Raihan, Mahmud Kamal
Baghdady, Micah
Dort, Heston
Bentor, Joseph
and
Xuan, Xiangchun
2023.
Fluid Elasticity-Enhanced Insulator-Based Dielectrophoresis for Sheath-Free Particle Focusing in Very Dilute Polymer Solutions.
Analytical Chemistry,
Vol. 95,
Issue. 43,
p.
16013.
Borthakur, Rajnandan
and
Ghosh, Uddipta
2023.
Electrophoretic trajectories of non-uniformly charged particles in viscoelastic fluids: the weak surface charge limit.
Journal of Fluid Mechanics,
Vol. 954,
Issue. ,
Dąda, Anna
Błaut, Paweł
Mikrut, Paweł
Kuniewski, Maciej
and
Zydroń, Paweł
2024.
Control of Dielectric Parameters of Micro- and Nanomodified Epoxy Resin Using Electrophoresis.
Energies,
Vol. 17,
Issue. 5,
p.
1095.
Borthakur, Rajnandan
and
Ghosh, Uddipta
2024.
Electrophoretic maneuvering of nonuniformly charged particles suspended in linear flows: Impact of the medium viscoelasticity.
Physical Review Fluids,
Vol. 9,
Issue. 2,
Liu, Lin
Zhang, Sen
Wang, Jihong
Feng, Libo
and
Xie, Chiyu
2024.
Construction of the absorbing boundary condition for the flow of Oldroyd-B fluid over a semi-infinite plate with magnetic effect.
Physics of Fluids,
Vol. 36,
Issue. 4,
Bentor, Joseph
and
Xuan, Xiangchun
2024.
Particle Size-Dependent Electrophoresis in Polymer Solutions.
Analytical Chemistry,
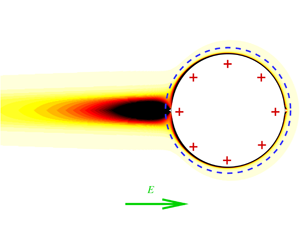
 $Wi$), which is the product of the polymer relaxation time and the shear rate, the polymers inside the double layer contribute to most of the velocity reduction by increasing the fluid viscosity. With increasing
$Wi$), which is the product of the polymer relaxation time and the shear rate, the polymers inside the double layer contribute to most of the velocity reduction by increasing the fluid viscosity. With increasing  $Wi$, viscoelasticity decreases and shear thinning increases the particle velocity. Polymer elasticity alters the fluid velocity disturbance outside the double layer from that of a neutral squirmer to a puller-type squirmer. At high
$Wi$, viscoelasticity decreases and shear thinning increases the particle velocity. Polymer elasticity alters the fluid velocity disturbance outside the double layer from that of a neutral squirmer to a puller-type squirmer. At high  $Wi$, the strong extensional stress inside the birefringent strand downstream of the particle dominates the velocity reduction. The scaling of the birefringent strand is used to estimate the particle velocity.
$Wi$, the strong extensional stress inside the birefringent strand downstream of the particle dominates the velocity reduction. The scaling of the birefringent strand is used to estimate the particle velocity.

