Hostname: page-component-848d4c4894-8kt4b Total loading time: 0 Render date: 2024-06-30T14:18:13.676Z Has data issue: false hasContentIssue false
  • English
  • Français

Effects of surface tension on a floating body in two dimensions

Published online by Cambridge University Press:  23 May 2018

Fei Zhang Open the ORCID record for Fei Zhang [Opens in a new window] ,
Xinping Zhou Open the ORCID record for Xinping Zhou [Opens in a new window]  and
Chengwei Zhu
Fei Zhang
Affiliation:
Department of Mechanics, Huazhong University of Science and Technology, Wuhan 430074, PR China
Xinping Zhou*
Affiliation:
Department of Mechanics, Huazhong University of Science and Technology, Wuhan 430074, PR China Hubei Key Laboratory for Engineering Structural Analysis and Safety Assessment, Wuhan 430074, PR China
Chengwei Zhu
Affiliation:
Department of Mechanics, Huazhong University of Science and Technology, Wuhan 430074, PR China
*
†Email address for correspondence: xpzhou08@hust.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

A model for calculating the force profile and the moment profile of a floating body in two dimensions with an arbitrary cross-section is proposed. Three types of cross-sections with different contact angles and densities are calculated by using the model to determine the vertical and rotational equilibria and their stabilities. Results show that the model can be applied to convex floating bodies with finitely many sharp edges. The study is then extended to investigate the surface tension effects on the vertical and rotational stabilities by varying the following parameters: the radii of curvature of the solid surface at the contact lines and the size of floating body. In general, the smaller the radii of curvature the better the vertical and rotational stabilities. However, for the contact angle 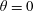$\unicode[STIX]{x1D703}=0$ (or 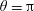$\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}$) the radii of curvature have no effect on the vertical stability of the floating body. By varying the size of the floating body, it is found that the vertical and rotational stabilities of mesoscale floating bodies vary continuously between the stabilities of the macroscale and microscale floating bodies with other parameters remaining unchanged.

JFM classification

Interfacial Flows (free surface): Capillary flows Mathematical Foundations: Mathematical Foundations Mathematical Foundations: Variational methods
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 847 , 25 July 2018 , pp. 489 - 519
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aspley, A., He, C. & McCuan, J. 2015 Force profiles for parallel plates partially immersed in a liquid bath. J. Math. Fluid Mech. 17, 87–102.Google Scholar
Bhatnagar, R. & Finn, R. 2006 Equilibrium configurations of an infinite cylinder in an unbounded fluid. Phys. Fluids 18, 047103.Google Scholar
Bhatnagar, R. & Finn, R. 2016 On the capillarity equation in two dimensions. J. Math. Fluid Mech. 18, 731–738.Google Scholar
Biran, A. 2003 Basic ship hydrostatics. In Ship Hydrostatics and Stability, pp. 23–70. Butterworth–Heinemann.Google Scholar
Bowden, N., Terfort, A., Carbeck, J. & Whitesides, G. M. 1997 Self-assembly of mesoscale objects into ordered two-dimensional arrays. Science 276, 233–235.Google Scholar
Brakke, K. A. 1992 The surface evolver. Exp. Math. 1, 141–165.Google Scholar
Chan, D. Y. C., Henry, J. D. & White, L. R. 1981 The interaction of colloidal particles collected at fluid interfaces. J. Colloid Interface Sci. 79, 410–418.Google Scholar
Chen, H. & Siegel, D. J. 2018 A floating cylinder on an unbounded bath. J. Math. Fluid Mech.; doi:10.1007/s00021-018-0372-7 In press. First Online: 28 March 2018.Google Scholar
Concus, P. 1968 Static menisci in a vertical right circular cylinder. J. Fluid Mech. 34, 481–495.Google Scholar
Finn, R. 1988 Non uniqueness and uniqueness of capillary surfaces. Manuscr. Math. 61, 347–372.CrossRefGoogle Scholar
Finn, R. 2010 On Young’s paradox, and the attractions of immersed parallel plates. Phys. Fluids 22, 017103.Google Scholar
Huh, C. & Mason, S. G. 1974 The flotation of axisymmetric particles at horizontal liquid interfaces. J. Colloid Interface Sci. 47, 271–289.Google Scholar
Janssens, S., Chaurasia, V. & Fried, E. 2017 Effect of a surface tension imbalance on a partly submerged cylinder. J. Fluid Mech. 830, 369–386.Google Scholar
Keller, J. B. 1998 Surface tension force on a partly submerged body. Phys. Fluids 10, 3009–3010.Google Scholar
Kemp, T. M. & Siegel, D. 2011 Floating bodies in two dimensions without gravity. Phys. Fluids 23, 043303.Google Scholar
Kralchevsky, P. A., Paunov, V. N., Ivanov, I. B. & Nagayama, K. 1992 Capillary meniscus interaction between colloidal particles attached to a liquid – fluid interface. J. Colloid Interface Sci. 151, 79–94.Google Scholar
Liu, J. L., Feng, X. Q. & Wang, G. F. 2007 Buoyant force and sinking conditions of a hydrophobic thin rod floating on water. Phys. Rev. E 76, 066103.Google Scholar
Majumdar, S. R. & Michael, D. H. 1976 The equilibrium and stability of two dimensional pendent drops. Proc. R. Soc. Lond. A 351, 89–115.Google Scholar
Mansfield, E. H., Sepangi, H. R. & Eastwood, E. A. 1997 Equilibrium and mutual attraction or repulsion of objects supported by surface tension. Phil. Trans. R. Soc. Lond. A 355, 869–919.Google Scholar
Miersemann, E.2015 Lecture Notes, ‘Liquid Interfaces’, Version November 2015, pp. 54–56. See http://www.math.uni-leipzig.de/∼miersemann/.Google Scholar
Nicolson, M. M. 1949 The interaction between floating particles. Proc. Camb. Phil. Soc. 45, 288–295.Google Scholar
Oettel, M., Dominguez, A. & Dietrich, S. 2005 Effective capillary interaction of spherical particles at fluid interfaces. Phys. Rev. E 71, 051401.Google Scholar
Oliver, J. F., Huh, C. & Mason, S. G. 1977 Resistance to spreading of liquids by sharp edges. J. Colloid Interface Sci. 59, 568–581.Google Scholar
Padday, J. F. 1971 The profiles of axially symmetric menisci. Phil. Trans. R. Soc. Lond. A 269, 265–293.Google Scholar
Paunov, V. N., Kralchevsky, P. A., Denkov, N. D., Ivanov, I. B. & Nagayama, K. 1992 Capillary meniscus interaction between a microparticle and a wall. Colloid Surf. 67, 119–138.Google Scholar
Princen, H. M. 1969 The equilibrium shape of interfaces, drops, and bubbles. Rigid and deformable particles at interfaces. In Surface and Colloid Science (ed. Matijević, E.), vol. 2, pp. 1–84. Wiley.Google Scholar
Rapacchietta, A. V., Neumann, A. W. & Omenyi, S. N. 1977 Force and free-energy analyses of small particles at fluid interfaces: I. Cylinders. J. Colloid Interface Sci. 59, 541–554.Google Scholar
Raphaël, E., Di Meglio, J. M., Berger, M. & Calabi, E. 1992 Convex particles at interfaces. J. Phys. I 2, 571–579.Google Scholar
Singh, P. & Hesla, T. I. 2004 The interfacial torque on a partially submerged sphere. J. Colloid Interface Sci. 280, 542–543.Google Scholar
Soligno, G., Dijkstra, M. & Van Roij, R. 2014 The equilibrium shape of fluid–fluid interfaces: Derivation and a new numerical method for Young’s and Young–Laplace equations. J. Chem. Phys. 141, 244702.Google Scholar
Soligno, G., Dijkstra, M. & Van Roij, R. 2016 Self-assembly of cubes into 2D hexagonal and honeycomb lattices by hexapolar capillary interactions. Phys. Rev. Lett. 116, 258001.Google Scholar
Stamou, D., Duschl, C. & Johannsmann, D. 2000 Long-range attraction between colloidal spheres at the air–water interface: The consequence of an irregular meniscus. Phys. Rev. E 62, 5263–5272.Google Scholar
Tavacoli, J. W., Katgert, G., Kim, E. G., Cates, M. E. & Clegg, P. S. 2012 Size limit for particle-stabilized emulsion droplets under gravity. Phys. Rev. Lett. 108, 268306.Google Scholar
Treinen, R. 2016 Examples of non-uniqueness of the equilibrium states for a floating Ball. Adv. Mater. Phys. Chem. 6, 177–194.Google Scholar
Vella, D. 2015 Floating versus sinking. Annu. Rev. Fluid Mech. 47, 115–135.Google Scholar
Vella, D., Lee, D. G. & Kim, H. Y. 2006 The load supported by small floating objects. Langmuir 22, 5979–5981.CrossRefGoogle ScholarPubMed
Zhou, X. & Zhang, F. 2017 Bifurcation of a partially immersed plate between two parallel plates. J. Fluid Mech. 817, 122–137.CrossRefGoogle Scholar

Zhang et al. supplementary movie 1

The vertical displacement of the selected shape.

Download Zhang et al. supplementary movie 1(Video)
Video 784.2 KB

Zhang et al. supplementary movie 2

The rotational displacement of the selected shape.

Download Zhang et al. supplementary movie 2(Video)
Video 2.3 MB