Article contents
Effects of geometry on resistance in elliptical pipe flows
Published online by Cambridge University Press: 18 March 2020
Abstract
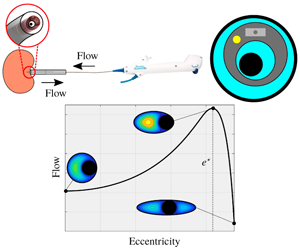
This paper considers the significant role of cross-sectional geometry on resistance in co-axial pipe flows. We consider an axially flowing viscous fluid in between two long and thin elliptical coaxial cylinders, one inside the other. The outer cylinder is stationary, while the inner cylinder (rod) is free to move. The rod poses a resistance to the axial flow, while the viscous fluid poses a resistance to any motion of the rod. We show that the equations for flow in the axial direction – driven by a prescribed flux – and for flow within the cross-section of the domain – driven by the motion of the rod – decouple in the asymptotic limit of small cylinder aspect ratio into axial Poiseuille flow and transverse Stokes flow, respectively. The objective of this paper is to calculate numerically the axial and cross-sectional resistances and to determine their dependence on cross-sectional geometry – i.e. rod position and the ellipticities of the rod and bounding cylinder. We characterise axial resistance, first for three reduced parameter spaces that have not been fully analysed in the literature: (i) a circle in an ellipse, (ii) an ellipse in a circle and (iii) an ellipse in an ellipse of equal eccentricity and orientation, before extending our geometric parameter space to determine the overall optimal geometry to minimise axial flow resistance for fixed cross-sectional area. Cross-sectional resistance is characterised via coefficients in a Stokes resistance matrix and we highlight the interdependent effects of cross-sectional ellipticity and boundary interactions.
JFM classification
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press
References
- 9
- Cited by


