Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-26T19:21:38.568Z Has data issue: false hasContentIssue false
  • English
  • Français

Effective stress jump across membranes

Published online by Cambridge University Press:  01 April 2020

Giuseppe A. Zampogna Open the ORCID record for Giuseppe A. Zampogna [Opens in a new window]  and
François Gallaire Open the ORCID record for François Gallaire [Opens in a new window]
Giuseppe A. Zampogna*
Affiliation:
Laboratory of Fluid Mechanics and Instabilities, École Polytechnique Fédérale de Lausanne, CH-1015Lausanne, Switzerland
François Gallaire
Affiliation:
Laboratory of Fluid Mechanics and Instabilities, École Polytechnique Fédérale de Lausanne, CH-1015Lausanne, Switzerland
*
†Email address for correspondence: giuseppe.zampogna@epfl.ch
Get access Rights & Permissions [Opens in a new window]

Abstract

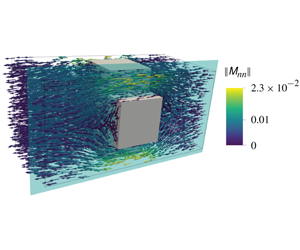
A macroscopic condition to simulate the interaction between an incompressible fluid flow and a permeable micro-structured rigid surface (i.e. a thin membrane) has been developed using multiscale homogenization and matching asymptotic expansions between the near membrane and the far region. The condition allows us to write the fluid velocity across the membrane, seen macroscopically as a smooth equivalent surface, as an effective jump between the stresses computed on the two faces of this surface. The coefficients appearing in the jump condition are the entries of tensors which solve Stokes problems within the pores, enforced by boundary conditions depending on the flow outside the membrane. These problems, found via homogenization, definitely characterize the microscopic geometrical properties of thin permeable micro-structured sheets. The new macroscopic model is validated by comparisons with direct numerical simulations of the fluid flow across membranes in different configurations, proving that the formalism adopted to write the jump conditions is valid. As a result, a rational tool able to join a microscopic and a macroscopic analysis of fluid flows across membranes is delivered, showing some potentialities to provide advancement in membrane design. It suggests that the concept of permeability has to be substituted by a more general tensor, called here the Navier tensor, which plays the role of permeability only in some particular situations.

JFM classification

Biological Fluid Dynamics: Membranes Low-Reynolds-number flows: Porous media
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 892 , 10 June 2020 , A9
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Achdou, Y., Le Tallec, P., Valentin, F. & Pironneau, O. 1998a Constructing wall laws with domain decomposition or asymptotic expansion techniques. Comput. Meth. Appl. Mech. Engng 151, 215–232.CrossRefGoogle Scholar
Achdou, Y., Pironneau, O. & Valentin, F. 1998b Effective boundary conditions for laminar flows over periodic rough boundaries. J. Comput. Phys. 147, 187–218.CrossRefGoogle Scholar
Alinovi, E., Gribaudo, M. & Bottaro, A. 2018 Fractal riblets. AIAA J. 56 (6), 2108–2112.CrossRefGoogle Scholar
Bacchin, P. 2017 Colloid-interface interactions initiates osmotic flow dynamics. Colloid Surf. A 533, 147–158.CrossRefGoogle Scholar
Bottaro, A. 2019 Flow over natural or engineered surfaces: an adjoint homogenization perspective. J. Fluid Mech. 877 (P1), 1–91.CrossRefGoogle Scholar
Bourgeat, A., Gipouloux, O. & Marusic-Paloka, E. 2001 Mathematical modelling and numerical simulation of a non-newtonian viscous flow through a thin filter. SIAM J. Appl. Maths 62, 597–626.CrossRefGoogle Scholar
Bourgeat, A., Marusic, S. & Marusic-Paloka, E. 1997 Ecoulement non newtonien travers un filtre mince. C. R. Acad. Sci. Paris I 324, 945–950.CrossRefGoogle Scholar
Bourgeat, A. & Marusic-Paloka, E. 1998 Mathematical modelling of a non-newtonian viscous flow through a thin filter. C. R. Acad. Sci. Paris I 327, 607–612.CrossRefGoogle Scholar
Brunn, P. O. 1984 Interaction between pores in diffusion through membranes of arbitrary thickness. J. Membr. Sci. 19, 117–136.CrossRefGoogle Scholar
Bucs, S. S., Valladares Linares, R., Vrouwenvelder, J. S. & Picioreanu, C. 2016 Biofouling in forward osmosis systems: an experimental and numerical study. Water Res. 106, 86–97.CrossRefGoogle ScholarPubMed
Cardoso, S. S. S. & Cartwright, J. H. E. 2014 Dynamics of osmosis in a porous medium. R. Soc. Open Sci. 1, 140352.CrossRefGoogle Scholar
Carraro, T., Goll, C., Marciniak-Czochra, A. & Mikelić, A. 2015 Effective interface conditions for the forced infiltration of a viscous fluid into a porous medium using homogenization. Comput. Meth. Appl. Mech. Engng 292, 195–220.CrossRefGoogle Scholar
Chou, S., Wang, R. & Fane, A. G. 2013 Robust and high performance hollow fiber membranes for energy harvesting from salinity gradients by pressure retarded osmosis. J. Membr. Sci. 448, 44–54.CrossRefGoogle Scholar
Conca, C. 1987a Etude d’un fluide traversant une paroi perforee. I. Comportement limite loin de la paroi. J. Math. Pures Appl. 66, 45–69.Google Scholar
Conca, C. 1987b Etude d’un fluide traversant une paroi perforee. I. Comportement limite pres de la paroi. J. Math. Pures Appl. 66, 1–43.Google Scholar
Darcy, H. 1856 Les fontaines publiques de la ville de Dijon: exposition et application des principes a suivre et des formules a employer dans les questions de distribution d’eau. Victor Dalmont.Google Scholar
Elimelech, M. & Phillip, W. 2011 The future of seawater desalination: energy, technology, and the environment. Science 333, 712–717.CrossRefGoogle ScholarPubMed
Farahbakhsh, J., Delnavaz, M. & Vatanpour, V. 2017 Investigation of raw and oxidized multiwalled carbon nanotubes in fabrication of reverse osmosis polyamide membranes for improvement in desalination and antifouling properties. Desalination 410, 1–9.CrossRefGoogle Scholar
Fritzmann, C., Lowenberg, J., Wintgens, T. & Melin, T. 2007 State-of-the-art of reverse osmosis desalination. Desalination 216, 1–76.CrossRefGoogle Scholar
Gravelle, S., Joly, L., Detcheverry, F., Ybert, C., Cottin-Bizonne, C. & Bocquet, L. 2013 Optimizing water permeability through the hourglass shape of aquaporins. Proc. Natl Acad. Sci. USA 110, 16367–16372.CrossRefGoogle ScholarPubMed
Hornung, U. 1997 Homogenization and Porous Media. Springer.CrossRefGoogle Scholar
Jensen, K. H., André, X. C. N. & Stone, H. A. 2014 Flow rate through microfilters: influence of the pore size distribution, hydrodynamic interactions, wall slip and inertia. Phys. Fluids 26, 052004.CrossRefGoogle Scholar
Jensen, K. H., Berg-Sørensen, K., Bruus, H., Holbrook, N. M., Liesche, J., Schulz, A., Zwieniecki, M. A. & Bohr, T. 2016 Sap flow and sugar transport in plants. Rev. Mod. Phys. 88, 035007.Google Scholar
Jiang, Z., Karan, S. & Livingston, A. G. 2018 Water transport through ultrathin polyamide nanofilms used for reverse osmosis. Adv. Mater. 30, 1705973.Google ScholarPubMed
Jiménez Bolaños, S. & Vernescu, B. 2017 Derivation of the navier slip and slip length for viscous flows over a rough boundary. Phys. Fluids 29, 057103.CrossRefGoogle Scholar
Kamrin, K. & Stone, H. A. 2011 The symmetry of mobility laws for viscous flow along arbitrarily patterned surfaces. Phys. Fluids 23, 031701.CrossRefGoogle Scholar
Karan, S., Jiang, Z. & Livingston, A. G. 2015 Sub-10 nm polyamide films with ultrafast solvent transport for molecular separation. Science 348, 1347–1351.CrossRefGoogle Scholar
Kedem, O. & Katchalsky, A. 1958 Thermodynamic analysis of the permeability of biological membranes to non-electrolytes. Biochim. Biophys. Acta 27, 229–246.CrossRefGoogle ScholarPubMed
Korneev, S. & Battiato, I. 2016 Sequential homogenization of reactive transport in polydisperse porous media. Multiscale Model. Simul. 14 (4), 1301–1318.CrossRefGoogle Scholar
Lācis, U. & Bagheri, S. 2017 A framework for computing effective boundary conditions at the interface between free fluid and a porous medium. J. Fluid Mech. 812, 866–889.CrossRefGoogle Scholar
Lācis, U., Sudhakar, Y., Pasche, S. & Bagheri, S. 2020 Transfer of mass and momentum at rough and porous surfaces. J. Fluid Mech. 884, A21.CrossRefGoogle Scholar
Ledesma-Duran, A., Hernández, S. I. & Santamaría-Holek, I. 2016 Generalized FJ approach for describing absorption desorption kinetics in irregular pores under nonequilibrium conditions. J. Phys. Chem. C 120, 7818–7821.CrossRefGoogle Scholar
Ledesma-Duran, A., Hernández, S. I. & Santamaría-Holek, I. 2017 Relation between the porosity and tortuosity of a memnbrane formed by connected irregular pores and the spatial diffusion coefficient of the FJ model. Phys. Rev. E 95, 052804.Google Scholar
Liu, Y., Xu, H., Dai, W., Li, H. & Wang, W. 2018 2.5-dimensional parylene c micropore array with a large area and a high porosity for high-throughput particle and cell separation. Microsyst. Nanoengng 4 (13), 1–12.Google Scholar
Malone, G. H., Hutchinson, T. E. & Prager, S. 1974 Molecular models for permeation through thin membranes: the effect of hydrodynamic interaction on permeability. J. Fluid Mech. 65 (4), 753–767.CrossRefGoogle Scholar
Matin, A., Khan, Z., Zaidia, S. M. J. & Boyce, M. C. 2011 Biofouling in reverse osmosis membranes for seawater desalination: phenomena and prevention. Desalination 281, 1–16.CrossRefGoogle Scholar
Mei, C. C. & Vernescu, B. 2010 Homogenization Methods for Multiscale Mechanics. World Scientific.CrossRefGoogle Scholar
Melnikov, D. V., Hulings, Z. H. & Gracheva, M. E. 2017 Electro-osmotic flow through nanopores in thin and ultrathin membranes. Phys. Rev. E 95, 063105.Google ScholarPubMed
Mohammadi, B., Pironneau, O. & Valentin, F. 1998 Rough boundaries and wall laws. Intl J. Numer. Meth. Fluids 27, 169–177.3.0.CO;2-4>CrossRefGoogle Scholar
Mohanty, K. & Purkait, M. K. 2011 Membrane Technologies and Applications. Taylor & Francis Group.CrossRefGoogle Scholar
Novoselov, K. S., Geim, A. K., Morozov, S. V., Jiang, D., Zhang, Y., Dubonos, S. V., Grigorieva, I. V. & Firsov, A. A. 2004 Electric field effect in atomically thin carbon films. Science 306 (569), 666–669.CrossRefGoogle ScholarPubMed
Ochoa-Tapia, J. A. & Whitaker, S. 1995 Momentum transfer at the boundary between a porous medium and a homogeneous fluid – I. Theoretical development. Intl J. Heat Mass Transfer 38 (14), 2635–2646.CrossRefGoogle Scholar
Park, H. B., Kamcev, J., Robeson, L. M., Elimelech, M. & Freeman, B. D. 2017 Maximizing the right stuff: the trade-off between membrane permeability and selectivity. Science 356 (6343), eaab0530.CrossRefGoogle ScholarPubMed
Pasquier, S., Quintard, M. & Davit, Y. 2017 Modeling flow in porous media with rough surfaces: effective slip boundary conditions and application to structured packings. Chem. Engng Sci. 165, 131–146.CrossRefGoogle Scholar
Picchi, D. & Battiato, I. 2018 The impact of pore-scale flow regimes on upscaling of immiscible two-phase flow in porous media. Water Resour. Res. 54 (9), 6683–6707.CrossRefGoogle Scholar
Rahardianto, A., McCool, B. C. & Cohen, Y. 2010 Accelerated desupersaturation of reverse osmosis concentrate by chemically-enhanced seeded precipitation. Desalination 264, 256–267.CrossRefGoogle Scholar
Ramon, G., Agnon, Y. & Dosoretz, C. 2010 Dynamics of an osmotic backwash cycle. J. Membr. Sci. 364, 157–166.CrossRefGoogle Scholar
Rautenbach, R. & Albrecht, R. 1994 Membrane Processes. John Wiley & Sons.Google Scholar
Roh, I. J., Kim, J. J. & Park, S. Y. 2002 Mechanical properties and reverse osmosis performance of interfacially polymerized polyamide thin films. J. Membr. Sci. 197, 199–210.CrossRefGoogle Scholar
Sampson, R. A. 1891 On stokes’ current function. Phil. Trans. R. Soc. Lond. A 182, 449–518.Google Scholar
Shannon, M. A., Bohn, P. W., Elimelech, M., Georgiadis, J. G., Mariñas, B. J. & Mayes, A. M. 2008 Science and technology for water purification in the coming decades. Nature 452, 301–310.CrossRefGoogle ScholarPubMed
She, Q., Wei, J., Ma, N., Sim, V., Fane, A. G., Wang, R. & Tang, C. Y. 2016 Fabrication and characterization of fabric-reinforced pressure retarded osmosis membranes for osmotic power harvesting. J. Membr. Sci. 504, 75–88.CrossRefGoogle Scholar
Sholl, D. & Lively, R. P. 2016 Seven chemical separations to change the world. Nature 532 (7600), 435–437.CrossRefGoogle ScholarPubMed
Song, R., Stone, H. A., Jensen, K. H. & Lee, J. 2019 Pressure-driven flow across a hyperelastic porous membrane. J. Fluid Mech. 871, 742–754.CrossRefGoogle Scholar
Spiegler, K. S. & Kedem, O. 1966 Thermodynamics of hyperfiltration (reverse osmosis): criteria for efficient membranes. Desalination 1, 311–326.CrossRefGoogle Scholar
Sudhakar, Y., Lācis, U., Pasche, S. & Bagheri, S.2019 Higher order homnogenized boundary conditions for flows over rough and porous surfaces. Preprint, arXiv:1909.07125v1.Google Scholar
Tio, K. K. & Sadhal, S. S. 1994 Boundary conditions for stokes flows near a porous membrane. Appl. Sci. Res. 52, 1–20.CrossRefGoogle Scholar
Valdés-Parada, F. J., Aguilar-Madera, C. G., Ochoa-Tapia, J. A. & Goyeau, B. 2013 Velocity and stress jump conditions between a porous medium and a fluid. Adv. Water Resour. 62, 327–339.CrossRefGoogle Scholar
Veran, S., Aspa, Y. & Quintard, M. 2009 Effective boundary conditions for rough reactive walls in laminar boundary layers. Intl J. Heat Mass Transfer 52, 3712–3725.CrossRefGoogle Scholar
Wang, C. Y. 1994 Stokes flow through a thin screen with patterned holes. AIChE J. 40, 419–423.CrossRefGoogle Scholar
Weissberg, H. L. 1962 End correction for slow viscous flow through long tubes. Phys. Fluids 5, 1033–1036.CrossRefGoogle Scholar
Whitaker, S. 1998 The Method of Volume Averaging. Technion – Israel Institute of Technology.Google Scholar
Zampogna, G. A., Magnaudet, J. & Bottaro, A. 2019 Generalized slip condition over rough surfaces. J. Fluid Mech. 858, 407–436.CrossRefGoogle Scholar