Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-18T06:10:41.111Z Has data issue: false hasContentIssue false
  • English
  • Français

Effect of excitation frequency on flow characteristics around a square cylinder with a synthetic jet positioned at front surface

Published online by Cambridge University Press:  15 October 2019

Yuan Qu Open the ORCID record for Yuan Qu [Opens in a new window] ,
Jinjun Wang Open the ORCID record for Jinjun Wang [Opens in a new window] ,
Lihao Feng Open the ORCID record for Lihao Feng [Opens in a new window]  and
Xi He Open the ORCID record for Xi He [Opens in a new window]
Yuan Qu
Affiliation:
Key Laboratory of Fluid Mechanics (Beijing University of Aeronautics and Astronautics), Ministry of Education, Beijing 100191, China
Jinjun Wang*
Affiliation:
Key Laboratory of Fluid Mechanics (Beijing University of Aeronautics and Astronautics), Ministry of Education, Beijing 100191, China
Lihao Feng
Affiliation:
Key Laboratory of Fluid Mechanics (Beijing University of Aeronautics and Astronautics), Ministry of Education, Beijing 100191, China
Xi He
Affiliation:
Key Laboratory of Fluid Mechanics (Beijing University of Aeronautics and Astronautics), Ministry of Education, Beijing 100191, China
*
†Email address for correspondence: jjwang@buaa.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

The flow over a square cylinder controlled by a slot synthetic jet positioned at the front surface is investigated experimentally at different excitation frequencies. The Reynolds number based on the free-stream velocity and the side length of the square cylinder is 1000. The flow visualization was conducted using the laser-induced fluorescence technique. The velocity fields upstream and downstream of the square cylinder were measured synchronously with the two-dimensional time-resolved particle image velocimetry technique. Both the evolution of vortex structures and the characteristic frequencies of upstream and downstream flow fields are presented. The flow dynamics vary significantly with the excitation frequency at a fixed stroke length. During one excitation cycle, the synthetic jet vortex pair deflects to one side and later swings to the other side at a quite small excitation frequency of $f_{e}/f_{0}=0.6$, while it only deflects toward one side and does not turn to the other side at $f_{e}/f_{0}=1.0$. Compared with the natural case, the wake characteristics for the above two cases are not changed much by the synthetic jet adopted. At a moderate excitation frequency of 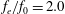$f_{e}/f_{0}=2.0$, the synthetic jet deflects upwards and downwards alternatively. The upstream flow field has a dominant frequency identical to half of the excitation frequency. Under the perturbations of the synthetic jet, two wake vortex pairs are formed per shedding cycle with a shedding frequency equal to that of the square cylinder without control. At a higher excitation frequency of 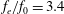$f_{e}/f_{0}=3.4$, the synthetic jet keeps deflecting to one side, and the upstream flow field is governed by the excitation frequency. The flow separation on the deflected side is suppressed effectively, and no periodic vortex shedding can be observed in the wake. Statistically, the velocity profiles also change with control. The recirculation bubble length in the wake is shortened, and the time-averaged velocity fluctuation is weakened remarkably. The control effects of the synthetic jet and the continuous jet are compared in this paper when placed at the front surface of a square cylinder.

JFM classification

Wakes/Jets: Separated flows Wakes/Jets: Wakes Vortex Flows: Vortex interactions
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 880 , 10 December 2019 , pp. 764 - 798
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Akansu, Y. E. & Firat, E. 2010a Control of flow around a square prism by slot jet injection from the rear surface. Exp. Therm. Fluid Sci. 34 (7), 906–914.Google Scholar
Akansu, Y. E. & Firat, E. 2010b Control of flow around a square prism by using synthetic jet. In Proceedings of the International Conference on Experimental Fluid Mechanics, 24–26 November 2010, Liberec, Czech Republic, pp. 14–29.Google Scholar
Akansu, Y. E., Firat, E. & Hacialioğullari, M. 2017 Reduction of fluid forces acting on a square prism using a planar jet. Exp. Therm. Fluid Sci. 86, 11–22.Google Scholar
Ali, M. S. M., Doolan, C. J. & Wheatley, V. 2011 Low Reynolds number flow over a square cylinder with a splitter plate. Phys. Fluids 23 (3), 033602–1.Google Scholar
Amitay, M. & Cannelle, F. 2006 Evolution of finite span synthetic jets. Phys. Fluids 18 (5), 054101.Google Scholar
Amitay, M., Honohan, A., Trautman, M. & Glezer, A.1997 Modification of the aerodynamic characteristics of bluff bodies using fluidic actuators. AIAA Paper 97-2004.Google Scholar
Anzai, Y., Fukagata, K., Meliga, P., Boujo, E. & Gallaire, F. 2017 Numerical simulation and sensitivity analysis of a low-Reynolds-number flow around a square cylinder controlled using plasma actuators. Phys. Rev. Fluids 2 (4), 043901.Google Scholar
Bearman, P. W. & Obasaju, E. D. 1982 An experimental study of pressure fluctuations on fixed and oscillating square-section cylinders. J. Fluid Mech. 119, 297–321.Google Scholar
Bearman, P. W. & Trueman, D. M. 1972 An investigation of the flow around rectangular cylinders. Aeronaut. Q. 23, 229–237.Google Scholar
Berkooz, G., Holmes, P. & Lumley, J. L. 1993 The proper orthogonal decomposition in the analysis of turbulent flows. Annu. Rev. Fluid Mech. 25 (1), 539–575.Google Scholar
Brika, D. & Laneville, A. 1993 Vortex-induced vibrations of a long flexible circular cylinder. J. Fluid Mech. 250, 481–508.Google Scholar
Brun, C. & Goossens, T. 2008 3D coherent vortices in the turbulent near wake of a square cylinder. C. R. Méc. 336 (4), 363–369.Google Scholar
Champagnat, F., Plyer, A., le Besnerais, G., Leclaire, B., Davoust, S. & le Sant, Y. 2011 Fast and accurate PIV computation using highly parallel iterative correlation maximization. Exp. Fluids 50 (4), 1169–1182.Google Scholar
Chatterjee, A. 2000 An introduction to the proper orthogonal decomposition. Curr. Sci. 78 (7), 808–817.Google Scholar
Chatterjee, D. & Gupta, S. K. 2015a Convective transport around a rotating square cylinder at moderate Reynolds numbers. Numer. Heat Tranfer. A 67 (12), 1386–1407.Google Scholar
Chatterjee, D. & Gupta, S. K. 2015b Numerical study of the laminar flow past a rotating square cylinder at low spinning rates. J. Fluids Engng 137 (2), 021204.Google Scholar
Deng, F., Xie, F., Huang, W., Dong, H. & Zhang, D. 2018 Numerical exploration on jet oscillation mechanism of counterflowing jet ahead of a hypersonic lifting-body vehicle. Sci. China-Technol. Sci. 61 (7), 1056–1071.Google Scholar
Deng, S. C., Pan, C., Wang, J. J. & Rinoshika, A. 2017 POD analysis of the instability mode of a low-speed streak in a laminar boundary layer. Acta Mech. Sin. 33 (6), 981–991.Google Scholar
Feng, L. H., Ma, L. Q. & Wang, J. J. 2014 End-effects of a finite synthetic jet on flow control. In Fluid-Structure-Sound Interactions and Control, pp. 129–134. Springer.Google Scholar
Feng, L. H. & Ran, L. K. 2018 Wavelet multi-scale analysis of the circular cylinder wake under synthetic jets control. Intl J. Heat Fluid Flow 69, 73–82.Google Scholar
Feng, L. H. & Wang, J. J. 2010 Circular cylinder vortex-synchronization control with a synthetic jet positioned at the rear stagnation point. J. Fluid Mech. 662, 232–259.Google Scholar
Feng, L. H. & Wang, J. J. 2014 Modification of a circular cylinder wake with synthetic jet: vortex shedding modes and mechanism. Eur. J. Mech. (B/Fluids) 43, 14–32.Google Scholar
Feng, L. H., Wang, J. J. & Pan, C. 2011 Proper orthogonal decomposition analysis of vortex dynamics of a circular cylinder under synthetic jet control. Phys. Fluids 23 (1), 014106.Google Scholar
Fu, Y. N., Zhao, X. Z., Cao, F. F., Zhang, D. K., Cheng, D. & Li, L. 2017 Numerical simulation of viscous flow past an oscillating square cylinder using a CIP-based model. J. Hydrodyn. 29 (1), 96–108.Google Scholar
Haller, G. 2002 Lagrangian coherent structures from approximate velocity data. Phys. Fluids 14 (6), 1851–1861.Google Scholar
Haller, G. 2015 Lagrangian coherent structures. Annu. Rev. Fluid Mech. 47, 137–162.Google Scholar
Hayashi, K., Aso, S. & Tani, Y. 2006 Experimental study on thermal protection system by opposing jet in supersonic flow. J. Spacecr. Rockets 43 (1), 233–235.Google Scholar
He, G. S., Li, N. & Wang, J. J. 2014 Drag reduction of square cylinders with cut-corners at the front edges. Exp. Fluids 55 (6), 1745.Google Scholar
He, G. S., Pan, C., Feng, L. H., Gao, Q. & Wang, J. J. 2016 Evolution of Lagrangian coherent structures in a cylinder-wake disturbed flat plate boundary layer. J. Fluid Mech. 792, 274–306.Google Scholar
Hsu, C. M., Huang, R. F. & Chung, H. C. 2016 Flow characteristics and drag force of a square cylinder in crossflow modulated by a slot jet injected from upstream surface. Exp. Therm. Fluid Sci. 75, 235–248.Google Scholar
Hu, J. C., Zhou, Y. & Dalton, C. 2006 Effects of the corner radius on the near wake of a square prism. Exp. Fluids 40 (1), 106–118.Google Scholar
Huang, R. F., Hsu, C. M. & Chen, Y. T. 2017 Modulating flow and aerodynamic characteristics of a square cylinder in crossflow using a rear jet injection. Phys. Fluids 29 (1), 015103.Google Scholar
Huang, R. F., Hsu, C. M. & Chiu, P. C. 2014 Flow behavior around a square cylinder subject to modulation of a planar jet issued from upstream surface. J. Fluids Struct. 51, 362–383.Google Scholar
Huang, W. 2015 A survey of drag and heat reduction in supersonic flows by a counterflowing jet and its combinations. J. Zhejiang Univ.-Sci. A 16 (7), 551–561.Google Scholar
Huang, Y. & Green, M. A. 2015 Detection and tracking of vortex phenomena using Lagrangian coherent structures. Exp. Fluids 56 (7), 147.Google Scholar
Igarashi, T. 1997 Drag reduction of a square prism by flow control using a small rod. J. Wind Engng Ind. Aerodyn. 69, 141–153.Google Scholar
Jiang, H., Cheng, L. & An, H. 2018 Three-dimensional wake transition of a square cylinder. J. Fluid Mech. 842, 102–127.Google Scholar
Kim, D. H., Yang, K. S. & Eom, J. S. 2003 Confined vortex shedding past a square cylinder with a planar jet. JSME Intl. J. Ser. B: Fluids Therm. Engng 46 (2), 316–325.Google Scholar
Kline, S. J. & McClintock, F. A. 1953 Describing uncertainties in single-sample experiments. Mech. Eng. 75, 3–8.Google Scholar
Koochesfahani, M. M. 1989 Vortical patterns in the wake of an oscillating airfoil. AIAA J. 27 (9), 1200–1205.Google Scholar
Koutmos, P., Papailiou, D. & Bakrozis, A. 2004 Experimental and computational study of square cylinder wakes with two-dimensional injection into the base flow region. Eur. J. Mech. (B/Fluids) 23 (2), 353–365.Google Scholar
Krishna, S., Green, M. A. & Mulleners, K. 2018 Flowfield and force evolution for a symmetric hovering flat-plate wing. AIAA J. 56 (4), 1360–1371.Google Scholar
Lou, X., Zhou, T., Jiang, H. & Cheng, L. 2016 Direct numerical simulation of three-dimensional flow past a yawed square cylinder. In 12th International Conference on Heat Transfer, Fluid Mechanics and Thermodynamics, July 11–13, 2016 Costa de Sol, Spain.Google Scholar
Ma, L. Q., Feng, L. H., Pan, C., Gao, Q. & Wang, J. J. 2015 Fourier mode decomposition of PIV data. Sci. China-Technol. Sci. 58 (11), 1935–1948.Google Scholar
Ma, X., Karamanos, G.-S. & Karniadakis, G. E. 2000 Dynamics and low-dimensionality of a turbulent near wake. J. Fluid Mech. 410, 29–65.Google Scholar
Meyer, B., Nelson, H. F. & Riggins, D. W. 2001 Hypersonic drag and heat-transfer reduction using a forward-facing jet. J. Aircraft 38 (4), 680–686.Google Scholar
Pan, C., Wang, H. P. & Wang, J. J. 2013 Phase identification of quasi-periodic flow measured by particle image velocimetry with a low sampling rate. Meas. Sci. Technol. 24 (5), 055305.Google Scholar
Pan, C., Xue, D., Xu, Y., Wang, J. J. & Wei, R. J. 2015 Evaluating the accuracy performance of Lucas-Kanade algorithm in the circumstance of PIV application. Sci. China-Phys. Mech. Astron. 58 (10), 104704.Google Scholar
Perrin, R., Braza, M., Cid, E., Cazin, S., Barthet, A., Sevrain, A., Mockett, C. & Thiele, F. 2007 Obtaining phase averaged turbulence properties in the near wake of a circular cylinder at high Reynolds number using POD. Exp. Fluids 43, 341–355.Google Scholar
Perrin, R., Braza, M., Cid, E., Cazin, S., Moradei, F., Barthet, A., Sevrain, A. & Hoarau, Y. 2006 Near-wake turbulence properties in the high Reynolds number incompressible flow around a circular cylinder measured by two- and three-component PIV. Flow Turbul. Combust. 77, 185–204.Google Scholar
Qu, Y., Wang, J. J., Sun, M., Feng, L. H., Pan, C., Gao, Q. & He, G. S. 2017 Wake vortex evolution of square cylinder with a slot synthetic jet positioned at the rear surface. J. Fluid Mech. 812, 940–965.Google Scholar
Raffel, M., Willert, C. E., Scarano, F., Kähler, C. J., Wereley, S. T. & Kompenhans, J. 2018 Particle Image Velocimetry: A Practical Guide. Springer.Google Scholar
Saha, A. K. & Shrivastava, A. 2015 Suppression of vortex shedding around a square cylinder using blowing. Sadhana 40 (3), 769–785.Google Scholar
Schnipper, T., Andersen, A. & Bohr, T. 2009 Vortex wakes of a flapping foil. J. Fluid Mech. 633, 411–423.Google Scholar
Sciacchitano, A. & Wieneke, B. 2016 PIV uncertainty propagation. Meas. Sci. Technol. 27 (8), 084006.Google Scholar
Shadden, S. C., Dabiri, J. O. & Marsden, J. E. 2006 Lagrangian analysis of fluid transport in empirical vortex ring flows. Phys. Fluids 18 (4), 047105.Google Scholar
Shao, C. P. & Wei, Q. D. 2008 Control of vortex shedding from a square cylinder. AIAA J. 46 (2), 397–407.Google Scholar
Sirovich, L. 1987 Turbulence and the dynamics of coherent structures. I. Coherent structures. Q. Appl. Maths 45 (3), 561–571.Google Scholar
Smith, B. L. & Glezer, A. 1998 The formation and evolution of synthetic jets. Phys. Fluids 10 (9), 2281–2297.Google Scholar
Sohankar, A., Khodadadi, M. & Rangraz, E. 2015 Control of fluid flow and heat transfer around a square cylinder by uniform suction and blowing at low Reynolds numbers. Comput. Fluids 109, 155–167.Google Scholar
Sohankar, A. & Najafi, M. 2018 Control of vortex shedding, forces and heat transfer from a square cylinder at incidence by suction and blowing. Intl J. Therm. Sci. 129, 266–279.Google Scholar
Sohankar, A., Norberg, C. & Davidson, L. 1998 Low-Reynolds-number flow around a square cylinder at incidence: study of blockage, onset of vortex shedding and outlet boundary condition. Intl J. Numer. Methods Fluids 26, 39–56.Google Scholar
Sohankar, A., Norberg, C. & Davidson, L. 1999 Simulation of three-dimensional flow around a square cylinder at moderate Reynolds numbers. Phys. Fluids 11 (2), 288–306.Google Scholar
Ueda, Y., Kurata, M., Kida, T. & Iguchi, M. 2009 Visualization of flow past a square prism with cut-corners at the front-edge. J. Vis. 12 (4), 383–391.Google Scholar
van Hinsberg, N. P., Schewe, G. & Jacobs, M. 2018 Experimental investigation on the combined effects of surface roughness and corner radius for square cylinders at high Reynolds numbers up to 107 . J. Wind Engng Ind. Aerodyn. 173, 14–27.Google Scholar
van Oudheusden, B. W., Scarano, F., van Hinsberg, N. P. & Watt, D. W. 2005 Phase-resolved characterization of vortex shedding in the near wake of a square-section cylinder at incidence. Exp. Fluids 39, 86–98.Google Scholar
Wang, C., Tang, H., Duan, F. & Yu, S. C. M. 2016 Control of wakes and vortex-induced vibrations of a single circular cylinder using synthetic jets. J. Fluids Struct. 60, 160–179.Google Scholar
Wang, J. J. & Feng, L. H. 2018 Flow Control Techniques and Applications (Cambridge Aerospace Series). Cambridge University Press.Google Scholar
Wang, J. J., Feng, L. H. & Xu, C. J. 2007 Experimental investigations on separation control and flow structure around a circular cylinder with synthetic jet. Sci. China Ser. E: Technol. Sci. 50 (5), 550–559.Google Scholar
Wang, J. S., Feng, L. H., Wang, J. J. & Li, T. 2018 Görtler vortices in low-Reynolds-number flow over multi-element airfoil. J. Fluid Mech. 835, 898–935.Google Scholar
Weightman, J. L., Amili, O., Honnery, D., Soria, J. & Edgington-Mitchell, D. 2018 Signatures of shear-layer unsteadiness in proper orthogonal decomposition. Exp. Fluids 59 (12), 180.Google Scholar
Williamson, C. H. K. & Govardhan, R. 2008 A brief review of recent results in vortex-induced vibrations. J. Wind Engng Ind. Aerodyn. 96 (6–7), 713–735.Google Scholar
Williamson, C. H. & Roshko, A. 1988 Vortex formation in the wake of an oscillating cylinder. J. Fluids Struct. 2 (4), 355–381.Google Scholar
Yoon, H., Lee, H. J., Lee, B. J. & Jeung, I. S. 2018 Numerical study of the effects of a counterflow jet on the drag reduction of a blunt body in a hypersonic flow. Intl J. Aeronaut. Space Sci. 19, 828–835.Google Scholar
Zdero, R., Turan, Ö. F. & Havard, D. G. 1995 Toward understanding galloping: near-wake study of oscillating smooth and stranded circular cylinders in forced motion. Exp. Therm. Fluid Sci. 10, 28–43.Google Scholar
Zhang, P. F., Wang, J. J. & Feng, L. H. 2008 Review of zero-net-mass-flux jet and its application in separation flow control. Sci. China Ser. E: Technol. Sci. 51 (9), 1315–1344.Google Scholar
Zhang, P. F., Wang, J. J., Lu, S. F. & Mi, J. 2005 Aerodynamic characteristics of a square cylinder with a rod in a staggered arrangement. Exp. Fluids 38 (4), 494–502.Google Scholar
Zhang, Q. S., Liu, Y. Z. & Wang, S. F. 2014 The identification of coherent structures using proper orthogonal decomposition and dynamic mode decomposition. J. Fluids Struct. 49, 53–72.Google Scholar
Zhou, J., Adrian, R. J., Balachandar, S. & Kendall, T. M. 1999 Mechanisms for generating coherent packets of hairpin vortices in channel flow. J. Fluid Mech. 387, 353–396.Google Scholar