No CrossRef data available.
Article contents
Early-time periodic injection and extraction in an inclined confined aquifer
Published online by Cambridge University Press: 10 July 2015
Abstract
We consider the periodic injection and extraction of fluid from a horizontal line well in an inclined saturated aquifer of finite thickness, 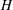 $H$, as part of an aquifer thermal energy storage system. We focus on the case in which the injected fluid is dense relative to the original fluid in the aquifer and hence tends to run off downslope, so that during the extraction cycle a mixture of original aquifer fluid and injected fluid is produced. We study the controls on the composition of the extracted fluid, distinguishing between the cases where there is an open boundary downslope or upslope of the source, with the other boundary being sealed. We find that initially the fraction of original aquifer fluid recovered during an extracted cycle decreases from cycle to cycle, and at long times this fraction asymptotes to a value,
$H$, as part of an aquifer thermal energy storage system. We focus on the case in which the injected fluid is dense relative to the original fluid in the aquifer and hence tends to run off downslope, so that during the extraction cycle a mixture of original aquifer fluid and injected fluid is produced. We study the controls on the composition of the extracted fluid, distinguishing between the cases where there is an open boundary downslope or upslope of the source, with the other boundary being sealed. We find that initially the fraction of original aquifer fluid recovered during an extracted cycle decreases from cycle to cycle, and at long times this fraction asymptotes to a value, 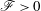 $\mathscr{F}>0$, that depends on
$\mathscr{F}>0$, that depends on 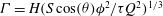 ${\it\Gamma}=H(S\cos ({\it\theta}){\it\phi}^{2}/{\it\tau}Q^{2})^{1/3}$ and
${\it\Gamma}=H(S\cos ({\it\theta}){\it\phi}^{2}/{\it\tau}Q^{2})^{1/3}$ and 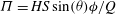 ${\it\Pi}=HS\sin ({\it\theta}){\it\phi}/Q$, where
${\it\Pi}=HS\sin ({\it\theta}){\it\phi}/Q$, where  ${\it\tau}$ is the time period of injection,
${\it\tau}$ is the time period of injection, 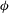 ${\it\phi}$ is the porosity of the aquifer,
${\it\phi}$ is the porosity of the aquifer, 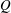 $Q$ is the injection rate,
$Q$ is the injection rate, 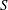 $S$ is the speed of the buoyancy driven flow and
$S$ is the speed of the buoyancy driven flow and 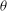 ${\it\theta}$ is the angle of inclination to the horizontal. At long times the flow asymptotes to a quasi-steady exchange flow solution that develops in an inclined saturated porous layer of thickness
${\it\theta}$ is the angle of inclination to the horizontal. At long times the flow asymptotes to a quasi-steady exchange flow solution that develops in an inclined saturated porous layer of thickness 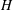 $H$ in contact with a stratified fluid reservoir, filled to thickness
$H$ in contact with a stratified fluid reservoir, filled to thickness 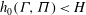 $h_{0}({\it\Gamma},{\it\Pi})<H$ with relatively dense fluid. This enables us to calculate the average composition of the extracted fluid, which is of concern if the original aquifer fluid contains contaminants. Since the produced aquifer fluid is driven by this quasi-steady exchange flow, we show that contaminants downslope of the well will be produced after a finite time, whereas contaminants upslope of the well typically remain in the aquifer, irrespective of the far-field boundary conditions. We successfully test the models with a series of analogue experiments of both the injection extraction flow and the exchange flow using a Hele-Shaw cell.
$h_{0}({\it\Gamma},{\it\Pi})<H$ with relatively dense fluid. This enables us to calculate the average composition of the extracted fluid, which is of concern if the original aquifer fluid contains contaminants. Since the produced aquifer fluid is driven by this quasi-steady exchange flow, we show that contaminants downslope of the well will be produced after a finite time, whereas contaminants upslope of the well typically remain in the aquifer, irrespective of the far-field boundary conditions. We successfully test the models with a series of analogue experiments of both the injection extraction flow and the exchange flow using a Hele-Shaw cell.
- Type
- Papers
- Information
- Copyright
- © 2015 Cambridge University Press



