Article contents
Early transition, relaminarization and drag reduction in the flow of polymer solutions through microtubes
Published online by Cambridge University Press: 10 January 2020
Abstract
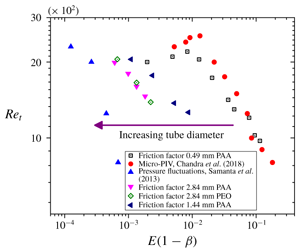
Experiments are performed to investigate the onset of early transition and drag reduction in the flow of polymer (polyacrylamide and polyethylene oxide) solutions through rigid microtubes of diameters in the range 0.49–2.84 mm. We measure friction factor variation with Reynolds number for varying polymer concentrations and tube diameters, and the Reynolds number,  $Re_{t}$, at which the experimental data deviate from the laminar value represents the onset of transition. Crucially, owing to the high shear rates encountered in our experiments, we show that it is important to account for shear thinning of the fluid in the theoretical estimation of the friction factor in the laminar regime. We accomplish this using a Carreau model, and show that the use of laminar friction factor calculated without shear thinning leads to an erroneous overestimation of
$Re_{t}$, at which the experimental data deviate from the laminar value represents the onset of transition. Crucially, owing to the high shear rates encountered in our experiments, we show that it is important to account for shear thinning of the fluid in the theoretical estimation of the friction factor in the laminar regime. We accomplish this using a Carreau model, and show that the use of laminar friction factor calculated without shear thinning leads to an erroneous overestimation of  $Re_{t}$. The
$Re_{t}$. The  $Re_{t}$ obtained from friction factor data in the present study is in good agreement with that inferred using micro particle image velocimetry analysis in Chandra et al. (J. Fluid Mech., vol. 844, 2018, pp. 1052–1083). For smaller concentrations of the added polymer, there is a marginal delay in the onset of turbulence, but as the concentration is increased further, the transition Reynolds number decreases much below
$Re_{t}$ obtained from friction factor data in the present study is in good agreement with that inferred using micro particle image velocimetry analysis in Chandra et al. (J. Fluid Mech., vol. 844, 2018, pp. 1052–1083). For smaller concentrations of the added polymer, there is a marginal delay in the onset of turbulence, but as the concentration is increased further, the transition Reynolds number decreases much below  $2000$, the usual value at which transition occurs in Newtonian pipe flows. Thus, the present study further corroborates the phenomenon of early transition leading to an ‘elasto-inertial’ turbulent state in the flow of polymer solutions. For concentrations such that there is a delay in transition, if
$2000$, the usual value at which transition occurs in Newtonian pipe flows. Thus, the present study further corroborates the phenomenon of early transition leading to an ‘elasto-inertial’ turbulent state in the flow of polymer solutions. For concentrations such that there is a delay in transition, if  $Re$ is maintained above the
$Re$ is maintained above the  $Re_{t}$ for Newtonian fluids, the flow is transitional or turbulent in the absence of polymers. At such a fixed
$Re_{t}$ for Newtonian fluids, the flow is transitional or turbulent in the absence of polymers. At such a fixed  $Re$, if the concentration of the polymer is increased gradually, the friction factor decreases and the flow relaminarizes. With further increase in polymer concentration, the flow undergoes a transition due to elasto-inertial instability. The effect of addition of small amounts of polymer on turbulent drag reduction in the flow of water through microtubes is also investigated. Increase in polymer concentration, molecular weight and decrease in tube diameter causes an increase in drag reduction. The friction factor data for different polymer concentrations, molecular weights, tube diameters and
$Re$, if the concentration of the polymer is increased gradually, the friction factor decreases and the flow relaminarizes. With further increase in polymer concentration, the flow undergoes a transition due to elasto-inertial instability. The effect of addition of small amounts of polymer on turbulent drag reduction in the flow of water through microtubes is also investigated. Increase in polymer concentration, molecular weight and decrease in tube diameter causes an increase in drag reduction. The friction factor data for different polymer concentrations, molecular weights, tube diameters and  $Re$, when plotted with
$Re$, when plotted with  $Wi(1-\unicode[STIX]{x1D6FD})$, show a reasonable collapse, where
$Wi(1-\unicode[STIX]{x1D6FD})$, show a reasonable collapse, where  $Wi$ is the Weissenberg number defined as the product of the longest relaxation time of the polymer solution and the average shear rate in the tube and
$Wi$ is the Weissenberg number defined as the product of the longest relaxation time of the polymer solution and the average shear rate in the tube and  $\unicode[STIX]{x1D6FD}$ is the ratio of solvent to total solution viscosity. Interestingly, the onset of the maximum drag reduction asymptote, for experiments using varying tube diameters and polymer concentrations, appears to occur at
$\unicode[STIX]{x1D6FD}$ is the ratio of solvent to total solution viscosity. Interestingly, the onset of the maximum drag reduction asymptote, for experiments using varying tube diameters and polymer concentrations, appears to occur at  $Wi(1-\unicode[STIX]{x1D6FD})\sim O(1)$.
$Wi(1-\unicode[STIX]{x1D6FD})\sim O(1)$.
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press
References
- 16
- Cited by


