Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-18T01:11:24.007Z Has data issue: false hasContentIssue false
  • English
  • Français

Dynamics of nearly spherical bubbles in a turbulent channel upflow

Published online by Cambridge University Press:  30 August 2013

Jiacai Lu  and
Gretar Tryggvason
Jiacai Lu
Affiliation:
Department of Mechanical Engineering, Worcester Polytechnic Institute, Worcester, MA 01609, USA
Gretar Tryggvason*
Affiliation:
Department of Aerospace and Mechanical Engineering, University of Notre Dame, Notre Dame, IN 46556, USA
*
†Email address for correspondence: gtryggva@nd.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

The dynamics of bubbles in upflow, in a vertical channel, is examined using direct numerical simulations (DNS), where both the flow and the bubbles are fully resolved. Two cases are simulated. In one case all the bubbles are of the same size and sufficiently small so they remain nearly spherical. In the second case, some of the small bubbles are coalesced into one large bubble. In both cases lift forces drive small bubbles to the wall, removing bubbles from the channel interior until the two-phase mixture is in hydrostatic equilibrium, and forming a bubble-rich wall layer. 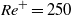The same evolution has been seen in earlier DNS of bubbly upflows, but here the friction Reynolds number is higher (${\mathit{Re}}^{+ } = 250$). In addition to showing that the overall structure persists at higher Reynolds numbers, we show that the bubbles in the wall layer form clusters. The mechanism responsible for the clustering is explained and how bubbles move into and out of the wall layer is examined. The dynamics of the bubbles in the channel core is also compared with results obtained in fully periodic domains and found to be similar. The presence of the large bubble disrupts the wall layer slightly, but does not change the overall picture much, for the parameters examined here.

JFM classification

Drops and Bubbles: Bubble dynamics Multiphase and Particle-laden Flows: Gas/liquid flow Multiphase and Particle-laden Flows: Multiphase flow
Type
Papers
Information
Journal of Fluid Mechanics , Volume 732 , 10 October 2013 , pp. 166 - 189
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Antal, S. P., Lahey, R. T. & Flaherty, J. E. 1991 Analysis of phase distribution in fully developed laminar bubbly two-phase flows. Intl J. Multiphase Flow 15, 635–652.Google Scholar
Azpitarte, O. E. & Buscaglia, G. C. 2003 Analytical and numerical evaluation of two-fluid model solutions for laminar fully developed bubbly two-phase flows. Chem. Engng Sci. 58, 3765–3776.Google Scholar
Biswas, S. & Tryggvason, G. 2007 The transient buoyancy driven motion of bubbles across a two-dimensional quiescent domain. Intl J. Multiphase Flow 33 (12), 1308–1319.Google Scholar
Bolotnov, I. A., Jansen, K. E., Drew, D. A., Oberai, A. A. Jr, Lahey, R. T. & Podowski, M. Z. 2011 Detached direct numerical simulations of turbulent two-phase bubbly channel flow. Intl J. Multiphase Flow 37, 647–659.Google Scholar
Bunner, B. & Tryggvason, G. 2002a Dynamics of homogeneous bubbly flows. Part 1. Rise velocity and microstructure of the bubbles. J. Fluid Mech. 466, 17–52.Google Scholar
Bunner, B. & Tryggvason, G. 2002b Dynamics of homogeneous bubbly flows. Part 2. Velocity fluctuations. J. Fluid Mech. 466, 53–84.Google Scholar
Bunner, B. & Tryggvason, G. 2003 Effect of bubble deformation on the stability and properties of bubbly flows. J. Fluid Mech. 495, 77–118.Google Scholar
Celik, I. & Gel, A. 2002 A new approach in modelling phase distribution in fully developed bubbly pipe flow. Flow Turbul. Combust. 68, 289–311.Google Scholar
Dabiri, S., Lu, J. & Tryggvason, G. 2012 Transition between regimes of a vertical channel bubbly upflow due to bubble deformability. (submitted).Google Scholar
Deckwer, W.-D. 1992 Bubble Column Reactors. Wiley.Google Scholar
Descamps, M. N., Oliemans, R. V. A., Ooms, G. & Mudde, R. F. 2008 Air–water flow in a vertical pipe: experimental study of air bubbles in the vicinity of the wall. Exp. Fluids 45, 357–370.Google Scholar
Dijkhuizen, W., Roghair, I., Annaland, M., Van Sint, & Kuipers, J. 2010a DNS of gas bubbles behaviour using an improved 3d front tracking model–drag force on isolated bubbles and comparison with experiments. Chem. Engng Sci. 65, 1415–1426.Google Scholar
Dijkhuizen, W., Roghair, I., Annaland, M., Van Sint, & Kuipers, J. 2010b DNS of gas bubbles behaviour using an improved 3d front tracking model–model development. Chem. Engng Sci. 65, 1427–1437.Google Scholar
Drew, D. A. & Lahey, R. T. Jr 1993 Analytical modelling of multiphase flow. In Particulate Two-phase Flow (ed. Roco, M. C.), pp. 509–566. Butterworth-Heinemann.Google Scholar
Drew, D. A. & Passman, S. L. 1999 Theory of Multicomponent Fluids. Springer.Google Scholar
Ervin, E. A. & Tryggvason, G. 1997 The rise of bubbles in a vertical shear flow. Trans. ASME: J. Fluids Engng 119, 443–449.Google Scholar
Esmaeeli, A. & Tryggvason, G. 1998 Direct numerical simulations of bubbly flows. Part 1. Low Reynolds number arrays. J. Fluid Mech. 377, 313–345.Google Scholar
Esmaeeli, A. & Tryggvason, G. 1999 Direct numerical simulations of bubbly flows. Part 2. Moderate Reynolds number arrays. J. Fluid Mech. 385, 325–358.Google Scholar
Esmaeeli, A. & Tryggvason, G. 2004 A front tracking method for computations of boiling in complex geometries. Intl J. Multiphase Flow 30, 1037–1050.Google Scholar
Esmaeeli, A. & Tryggvason, G. 2005 A direct numerical simulation study of the buoyant rise of bubbles at O(100) Reynolds number. Phys. Fluids 17, 093303.Google Scholar
Figueroa-Espinoza, B. & Zenit, R. 2005 Clustering in high Re monodispersed bubbly flows. Phys. Fluids 17, 091701.Google Scholar
Furusaki, S., Fan, L.-S. & Garside, J. 2001 The Expanding World of Chemical Engineering, 2nd edn. Taylor and Francis.Google Scholar
Gibson, J. F., Halcrow, J. & Cvitanović, P. 2008 Visualizing the geometry of state space in plane Couette flow. J. Fluid Mech. 611, 107–130.Google Scholar
Guet, S., Ooms, G. & Oliemans, R. V. A. 2005 Simplified two-fluid model for gas-lift efficiency predictions. AIChE J. 51, 1885–1896.Google Scholar
Guet, S., Ooms, G., Oliemans, R. V. A. & Mudde, R. F. 2004 Bubble size effect on low liquid input drift-flux parameters. Chem. Engng Sci. 59, 3315–3329.Google Scholar
Hao, Y. & Prosperetti, A. 2004 A numerical method for three-dimensional gas–liquid flow computations. J. Comput. Phys. 196, 126–144.Google Scholar
Hua, J. & Lou, J. 2007 Numerical simulation of bubble rising in viscous liquid. J. Comput. Phys. 222, 769–795.Google Scholar
Ishii, M. 1975 Thermo-fluid Dynamic Theory of Two-phase Flows. Eyrolles.Google Scholar
Jeong, J. & Hussain, F. 1995 On the identification of a vortex. J. Fluid Mech. 285, 69–94.Google Scholar
Kashinsky, O. N. & Randin, V. V. 1999 Downward bubbly gas–liquid flow in a vertical pipe. Intl J. Multiphase Flow 25, 109–138.Google Scholar
Kataoka, I. & Serizawa, A. 1989 Basic equations of turbulence in gas liquid two-phase flow. Intl J. Multiphase Flow 12, 745–758.Google Scholar
Kuo, T. C., Pan, C. & Chieng, C. C. 1997 Eulerian–Lagrangian computations on phase distribution of two-phase bubbly flows. Intl J. Numer. Meth. Fluids 24, 579–593.Google Scholar
Liu, T. J. 1997 Investigation of the wall shear stress in vertical bubbly flow under different bubble size conditions. Intl J. Multiphase Flow 23, 1085–1109.Google Scholar
Liu, T. J. & Bankoff, S. G. 1993 Structure of air–water bubbly flow in a vertical pipe-I. Liquid mean velocity and turbulence measurements. Intl J. Heat Mass Transfer 36, 1049–1060.Google Scholar
Lopez De Bertodano, M. Jr, Lahey, R. T. & Jones, O. C. 1987 Development of a $k$ – $\epsilon $ model for bubbly two-phase flow. Trans. ASME: J. Fluids Engng 13, 327–343.Google Scholar
Lopez De Bertodano, M. Jr, Lahey, R. T. & Jones, O. C. 1994 Phase distribution in bubbly two-phase flow in vertical ducts. Intl J. Multiphase Flow 20, 805–818.Google Scholar
Lu, J., Biswas, S. & Tryggvason, G. 2006 A DNS study of laminar bubbly flows in a vertical channel. Intl J. Multiphase Flow 32, 643–660.Google Scholar
Lu, J., Fernandez, A. & Tryggvason, G. 2005 The effect of bubbles on the wall shear in a turbulent channel flow. Phys. Fluids 17, 095102.Google Scholar
Lu, J. & Tryggvason, G. 2006 Numerical study of turbulent bubbly downflows in a vertical channel. Phys. Fluids 18, 103302.Google Scholar
Lu, J. & Tryggvason, G. 2007 Effect of bubble size in turbulent bubbly downflow in a vertical channel. Chem. Engng Sci. 62, 3008–3018.Google Scholar
Lu, J. & Tryggvason, G. 2008 Effect of bubble deformability in turbulent bubbly upflow in a vertical channel. Phys. Fluids 20, 040701.Google Scholar
Matos, A., de Rosa, E. S. & Franca, F. A. 2004 The phase distribution of upward co-current bubbly flows in a vertical square channel. J. Braz. Soc. Mech. Sci. Engng 26, 308–316.Google Scholar
Mendez-Diaz, S., Zenit, R., Chiva, S., Muñoz-Cobo, J. L. & Martinez-Martinez, S. 2012 A criterion for the transition from wall to core peak gas volume fraction distributions in bubbly flows. Intl J. Multiphase Flow 43, 56–61.Google Scholar
Molin, D., Marchioli, C. & Soldati, A. 2012 Turbulence modulation and microbubble dynamics in vertical channel flow. Intl J. Multiphase Flow 42, 80–95.Google Scholar
Muradoglu, M. & Kayaalp, A. D. 2006 An auxiliary grid method for computations of multiphase flows in complex geometries. J. Comput. Phys. 214, 858–877.Google Scholar
Nakoryakov, V. E., Kashinsky, O. N., Randin, V. V. & Timkin, L. S. 1996 Gas–liquid bubbly flow in vertical pipes. Trans. ASME: J. Fluids Engng 118, 377–382.Google Scholar
Politano, M. S., Carrica, P. M. & Converti, J. 2003 A model for turbulent polydisperse two-phase flow in vertical channel. Intl J. Multiphase Flow 29, 1153–1182.Google Scholar
Prosperetti, A. & Tryggvason, G. 2007 Computational Methods for Multiphase Flow. Cambridge University Press.Google Scholar
Serizawa, A., Kataoka, I. & Michiyoshi, I. 1975a Turbulence structure of air–water bubbly flow-II. Local properties. Intl J. Multiphase Flow 2, 235–246.Google Scholar
Serizawa, A., Kataoka, I. & Michiyoshi, I. 1975b Turbulence structure of air–water bubbly flow-III. Transport properties. Intl J. Multiphase Flow 2, 247–259.Google Scholar
van Sint Annaland, M., Dijkhuizen, W., Deen, N. G. & Kuipers, J. A. M. 2006 Numerical simulation of gas bubbles behaviour using a 3D front tracking method. AIChE J. 52, 99–110.Google Scholar
So, S., Morikita, H., Takagi, S. & Matsumoto, Y. 2002 Laser doppler velocimetry measurement of turbulent bubbly channel flow. Exp. Fluids 33, 135–142.Google Scholar
Takagi, S. & Matsumoto, Y. 2011 Surfactant effects on bubble motion and bubbly flows. Annu. Rev. Fluid Mech. 43, 615–636.Google Scholar
Takagi, S., Ogasawara, T. & Matsumoto, Y. 2008 The effects of surfactant on the multiscale structure of bubbly flows. Phil. Trans. R. Soc. Lond. A 366, 2117–2129.Google Scholar
Tomiyama, A., Tamai, H., Zun, I. & Hosokawa, S. 2002 Transverse migration of single bubbles in simple shear flows. Chem. Engng Sci. 57, 1849–1858.Google Scholar
Tryggvason, G., Bunner, B., Esmaeeli, A., Juric, D., Al-Rawahi, N., Tauber, W., Han, J., Nas, S. & Jan, Y.-J. 2001 A front tracking method for the computations of multiphase flow. J. Comput. Phys. 169, 708–759.Google Scholar
Tryggvason, G., Scardovelli, R. & Zaleski, 2011 Direct Numerical Simulations of Gas-Liquid Multiphase Flow. Cambridge University Press.Google Scholar
Unverdi, S. O. & Tryggvason, G. 1992 A front-tracking method for viscous, incompressible, multi-fluid flows. J. Comput. Phys. 100, 25–37.Google Scholar
Wang, S. K., Lee, S. J. Jr, Jones, O. C. Jr & Lahey, R. T. 1987 3-D turbulence structure and phase distribution in bubbly two-phase flows. Intl J. Multiphase Flow 13, 327–343.Google Scholar
Zhang, D. Z. & Prosperetti, A. 1994 Ensemble phase-averaged equations for bubbly flows. Phys. Fluids 6, 2956–2970.Google Scholar