Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-22T01:10:52.541Z Has data issue: false hasContentIssue false
  • English
  • Français

A dissipative random velocity field for fully developed fluid turbulence

Published online by Cambridge University Press:  04 April 2016

Rodrigo M. Pereira Open the ORCID record for Rodrigo M. Pereira [Opens in a new window] ,
Christophe Garban  and
Laurent Chevillard
Rodrigo M. Pereira*
Affiliation:
Univ Lyon, Ens de Lyon, Univ Claude Bernard, CNRS, Laboratoire de Physique, 46 allée d’Italie F-69342 Lyon, France CAPES Foundation, Ministry of Education of Brazil, Brasília/DF 70040-020, Brazil
Christophe Garban
Affiliation:
Université de Lyon, Institut Camille Jordan, 43 blvd. du 11 novembre 1918, F-69622 Villeurbanne CEDEX, France
Laurent Chevillard
Affiliation:
Univ Lyon, Ens de Lyon, Univ Claude Bernard, CNRS, Laboratoire de Physique, 46 allée d’Italie F-69342 Lyon, France
*
†Email address for correspondence: rodrigo.pereira@ens-lyon.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate the statistical properties, based on numerical simulations and analytical calculations, of a recently proposed stochastic model for the velocity field (Chevillard et al., Europhys. Lett., vol. 89, 2010, 54002) of an incompressible, homogeneous, isotropic and fully developed turbulent flow. A key step in the construction of this model is the introduction of some aspects of the vorticity stretching mechanism that governs the dynamics of fluid particles along their trajectories. 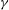An additional further phenomenological step aimed at including the long range correlated nature of turbulence makes this model dependent on a single free parameter, ${\it\gamma}$, that can be estimated from experimental measurements. We confirm the realism of the model regarding the geometry of the velocity gradient tensor, the power-law behaviour of the moments of velocity increments (i.e. the structure functions) including the intermittent corrections and the existence of energy transfer across scales. We quantify the dependence of these basic properties of turbulent flows on the free parameter 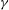${\it\gamma}$ and derive analytically the spectrum of exponents of the structure functions in a simplified non-dissipative case. A perturbative expansion in power of 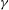${\it\gamma}$ shows that energy transfer, at leading order, indeed take place, justifying the dissipative nature of this random field.

JFM classification

Turbulent Flows: Intermittency Turbulent Flows: Isotropic turbulence Turbulent Flows: Turbulence modelling
Type
Papers
Information
Journal of Fluid Mechanics , Volume 794 , 10 May 2016 , pp. 369 - 408
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrian, R. & Moin, P. 1988 Stochastic estimation of organized turbulent structure: homogeneous shear flow. J. Fluid Mech. 190, 531–559.Google Scholar
Antonia, R. A., Phan Thien, N. & Satyaprakash, B. R. 1981 Autocorrelation and spectrum of dissipation fluctuations in a turbulent jet. Phys. Fluids 24, 554–555.Google Scholar
Arneodo, A., Bacry, E. & Muzy, J.-F. 1998 Random cascades on wavelet dyadic tree. J. Math. Phys. 39, 4142–4164.Google Scholar
Batchelor, G. K. 1953 The Theory of Homogeneous Turbulence. Cambridge University Press.Google Scholar
Benzi, R., Biferale, L., Crisanti, A., Paladin, G., Vergassola, M. & Vulpiani, A. 1993 A random process for the construction of multiaffine fields. Physica D 65, 352–358.Google Scholar
Biferale, L., Boffetta, G., Celani, A., Crisanti, A. & Vulpiani, A. 1998 Mimicking a turbulent signal: sequential multiaffine processes. Phys. Rev. E 57 (6), 6261–6264.Google Scholar
Çağlar, M. 2007 Velocity fields with power-law spectra for modeling turbulent flows. Appl. Math. Model. 31, 1934–1946.Google Scholar
Chen, S., Sreenivasan, K., Nelkin, M. & Cao, N. 1997 Refined similarity hypothesis for transverse structure functions in fluid turbulence. Phys. Rev. Lett. 79, 2253–2256.Google Scholar
Chevillard, L.2015 A random painting of fluid turbulence. Habilitation à diriger des recherches, ENS Lyon https://tel.archives-ouvertes.fr/tel-01212057.Google Scholar
Chevillard, L., Castaing, B., Arneodo, A., Lévêque, E., Pinton, J.-F. & Roux, S. 2012 A phenomenological theory of Eulerian and Lagrangian velocity fluctuations in turbulent flows. C. R. Physique 13, 899–928.Google Scholar
Chevillard, L., Lévêque, E., Taddia, F., Meneveau, C., Yu, H. & Rosales, C. 2011 Local and non local pressure Hessian effects in real and synthetic fluid turbulence. Phys. Fluids 23, 095108.Google Scholar
Chevillard, L., Rhodes, R. & Vargas, V. 2013 Gaussian multiplicative chaos for symmetric isotropic matrices. J. Stat. Phys. 150, 678–703.Google Scholar
Chevillard, L., Robert, R. & Vargas, V. 2010 A stochastic representation of the local structure of turbulence. Europhys. Lett. 89, 54002.Google Scholar
Constantin, P. 1994 Geometric statistics in turbulence. SIAM Rev. 36, 73–98.Google Scholar
Dhruva, B., Tsuji, Y. & Sreenivasan, K. 1997 Transverse structure functions in high-Reynolds-number turbulence. Phys. Rev. E 56, R4928–R4930.Google Scholar
Duchon, J. & Robert, R. 2000 Inertial energy dissipation for weak solutions of incompressible Euler and Navier–Stokes equations. Nonlinearity 13, 249–255.Google Scholar
Eyink, G. & Sreenivasan, K. 2006 Onsager and the theory of hydrodynamic turbulence. Rev. Mod. Phys. 78, 87–135.Google Scholar
Frigo, M. & Johnson, S. G. 2005 The design and implementation of fftw3. Proc. IEEE 93 (2), 216–231.Google Scholar
Frisch, U. 1995 Turbulence, The Legacy of A. N. Kolmogorov. Cambridge University Press.CrossRefGoogle Scholar
Gagne, Y. & Hopfinger, E. J. 1979 High order dissipation correlations and structure functions in an axisymmetric jet and a plane channel flow. In 2nd Symposium on Turbulent Shear Flows, Imperial College, London, 11.7–11.2.Google Scholar
Grauer, R., Homann, H. & Pinton, J.-F. 2012 Longitudinal and transverse structure functions in high-Reynolds-number turbulence. New J. Phys. 14, 063016.Google Scholar
Hedevang, E. & Schmiegel, A. 2014 A Lévy based approach to random vector fields: with a view towards turbulence. Intl J. Nonlinear Sci. Numer. Simul. 15, 411–435.CrossRefGoogle Scholar
Hill, R. 2001 Equations relating structure functions of all orders. J. Fluid Mech. 434, 379–388.Google Scholar
Juneja, A., Lathrop, D. P., Sreenivasan, K. R. & Stolovitzky, G. 1994 Synthetic turbulence. Phys. Rev. E 49 (6), 5179–5194.Google ScholarPubMed
Kahane, J.-P. 1985 Sur le chaos multiplicatif. Ann. Sci. Math. Québec 9, 105–150.Google Scholar
Kolmogorov, A. N. 1941 The local structure of turbulence in a incompressible viscous fluid for very large Reynolds number. Dokl. Akad. Nauk SSSR 30, 299–303.Google Scholar
Kolmogorov, A. N. 1962 A refinement of previous hypotheses concerning the local structure of turbulence in a viscous incompressible fluid at high Reynolds number. J. Fluid Mech. 13, 82–85.Google Scholar
Langford, J. & Moser, R. 1999 Optimal LES formulations for isotropic turbulence. J. Fluid Mech. 398, 321–346.Google Scholar
Majda, A. & Bertozzi, A. 2002 Vorticity and Incompressible Flow. Cambridge University Press.Google Scholar
Mandelbrot, B. B. 1972 Possible refinement of the lognormal hypothesis concerning the distribution of energy dissipation in intermittent turbulence. In Statistical Models and Turbulence (ed. Rosenblatt, M. & Van Atta, C.), Lecture Notes in Physics, vol. 12, pp. 333–351. Springer.Google Scholar
Mandelbrot, B. B. & Van Ness, J. W. 1968 Fractional Brownian motion, fractional noises and applications. SIAM Rev. 10, 422–437.Google Scholar
Meneveau, C. 2011 Lagrangian dynamics and models of the velocity gradient tensor in turbulent flows. Annu. Rev. Fluid Mech. 43, 219–245.Google Scholar
Monin, A. S. & Yaglom, A. M. 1971 Statistical Fluid Mechanics, vol. 1 & 2. MIT Press.Google Scholar
Nawroth, A. P. & Peinke, J. 2006 Multiscale reconstruction of time series. Phys. Lett. A 360, 234–237.Google Scholar
Obukhov, A. M. 1962 Some specific features of atmospheric turbulence. J. Fluid Mech. 13, 77–81.Google Scholar
Papoulis, A. 1991 Probability, Random Variables and Stochastic Processes, 3rd edn. McGraw-Hill International Editions.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Rhodes, R. & Vargas, V. 2014 Gaussian multiplicative chaos and applications: A review. Probability Surveys 11, 315–392.Google Scholar
Robert, R. & Vargas, V. 2008 Hydrodynamic turbulence and intermittent random fields. Comm. Math. Phys. 284, 649–673.Google Scholar
Rosales, C. & Meneveau, C. 2008 Anomalous scaling and intermittency in three-dimensional synthetic turbulence. Phys. Rev. E 78, 016313.Google Scholar
Schmiegel, J., Cleve, J., Eggers, H., Pearson, B. & Greiner, M. 2004 Stochastic energy-cascade model for (1+1)-dimensional fully developed turbulence. Phys. Lett. A 320, 247–253.CrossRefGoogle Scholar
Sidje, R. B. 1998 Expokit: A software package for computing matrix exponentials. ACM Trans. Math. Softw. 24 (1), 130–156.Google Scholar
Tennekes, H. & Lumley, J. L. 1972 A First Course in Turbulence. MIT Press.Google Scholar
Tsinober, A. 2001 An Informal Introduction to Turbulence. Kluwer.Google Scholar
Vieillefosse, P. 1982 Local interaction between vorticity and shear in a perfect incompressible fluid. J. Phys. (Paris) 43, 837–842.Google Scholar
Wallace, J. 2009 Twenty years of experimental and direct numerical simulation access to the velocity gradient tensor: What have we learned about turbulence? Phys. Fluids 21, 021301.CrossRefGoogle Scholar
Wilczek, M. & Meneveau, C. 2014 Pressure Hessian and viscous contributions to velocity gradient statistics based on Gaussian random fields. J. Fluid Mech. 756, 191–225.Google Scholar
Yakhot, V. 2001 Mean-field approximation and a small parameter in turbulence theory. Phys. Rev. E 63, 026307.Google Scholar