Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-17T23:10:42.029Z Has data issue: false hasContentIssue false
  • English
  • Français

Disruption of 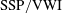$\text{SSP}/\text{VWI}$ states by a stable stratification

Published online by Cambridge University Press:  06 November 2015

T. S. Eaves  and
C. P. Caulfield
T. S. Eaves*
Affiliation:
DAMTP, University of Cambridge, Cambridge CB3 0WA, UK
C. P. Caulfield
Affiliation:
DAMTP, University of Cambridge, Cambridge CB3 0WA, UK BP Institute, University of Cambridge, Cambridge CB3 0EZ, UK
*
†Email address for correspondence: t.s.eaves@damtp.cam.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

We identify ‘minimal seeds’ for turbulence, i.e. initial conditions of the smallest possible total perturbation energy density 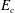$E_{c}$ that trigger turbulence from the laminar state, in stratified plane Couette flow, the flow between two horizontal plates of separation 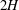$2H$, moving with relative velocity 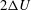$2{\rm\Delta}U$, across which a constant density difference 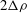$2{\rm\Delta}{\it\rho}$ from a reference density 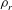${\it\rho}_{r}$ is maintained. To find minimal seeds, we use the ‘direct-adjoint-looping’ (DAL) method for finding nonlinear optimal perturbations that optimise the time-averaged total dissipation of energy in the flow. These minimal seeds are located adjacent to the edge manifold, the manifold in state space that separates trajectories which transition to turbulence from those which eventually decay to the laminar state. The edge manifold is also the stable manifold of the system’s ‘edge state’. Therefore, the trajectories from the minimal seed initial conditions spend a large amount of time in the vicinity of some states: the edge state; another state contained within the edge manifold; or even in dynamically slowly varying regions of the edge manifold, allowing us to investigate the effects of a stable stratification on any coherent structures associated with such states. In unstratified plane Couette flow, these coherent structures are manifestations of the self-sustaining process (SSP) deduced on physical grounds by Waleffe (Phys. Fluids, vol. 9, 1997, pp. 883–900), or equivalently finite Reynolds number solutions of the vortex–wave interaction (VWI) asymptotic equations initially derived mathematically by Hall & Smith (J. Fluid Mech., vol. 227, 1991, pp. 641–666). The stratified coherent states we identify at moderate Reynolds number display an altered form from their unstratified counterparts for bulk Richardson numbers 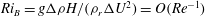$\mathit{Ri}_{B}=g{\rm\Delta}{\it\rho}H/({\it\rho}_{r}{\rm\Delta}U^{2})=O(\mathit{Re}^{-1})$, and exhibit chaotic motion for larger 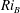$\mathit{Ri}_{B}$. We demonstrate that at hith Reynolds number the suppression of vertical motions by stratification strongly disrupts input from the waves to the roll velocity structures, thus preventing the waves from reinforcing the viscously decaying roll structures adequately, when 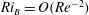$\mathit{Ri}_{B}=O(\mathit{Re}^{-2})$.

JFM classification

Instability: Nonlinear instability Instability: Transition to turbulence Mathematical Foundations: Variational methods
Type
Papers
Information
Journal of Fluid Mechanics , Volume 784 , 10 December 2015 , pp. 548 - 564
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bottin, S. & Chate, H. 1998 Statistical analysis of the transition to turbulence in plane Couette flow. Eur. Phys. J. B 6 (1), 143–155.CrossRefGoogle Scholar
Butler, K. M. & Farrell, B. F. 1992 Three-dimensional optimal perturbations in viscous shear flow. Phys. Fluids A 4 (8), 1637–1650.CrossRefGoogle Scholar
Chantry, M. & Schneider, T. M. 2014 Studying edge geometry in transiently turbulent shear flows. J. Fluid Mech. 747, 506–517.CrossRefGoogle Scholar
Cherubini, S., De Palma, P., Robinet, J.-C. & Bottaro, A. 2010 Rapid path to transition via nonlinear localized optimal perturbations in a boundary-layer flow. Phys. Rev. E 82, 066302.Google Scholar
Duguet, Y., Monokrousos, A., Brandt, L. & Henningson, S. 2013 Minimal transition thresholds in plane Couette flow. Phys. Fluids 25, 084103.CrossRefGoogle Scholar
Duguet, Y., Willis, A. P. & Kerswell, R. R. 2008 Transition in pipe flow: the saddle structure on the boundary of turbulence. J. Fluid Mech. 613, 255–274.CrossRefGoogle Scholar
Hall, P. & Sherwin, S. 2010 Streamwise vortices in shear flows: harbingers of transition and the skeleton of coherent structures. J. Fluid Mech. 661, 178–205.CrossRefGoogle Scholar
Hall, P. & Smith, F. T. 1991 On strongly nonlinear vortex/wave interactions in boundary-layer transition. J. Fluid Mech. 227, 641–666.CrossRefGoogle Scholar
Kerswell, R. R., Pringle, C. C. T. & Willis, A. P. 2014 An optimisation approach for analysing nonlinear stability with transition to turbulence in fluids as an exemplar. Rep. Prog. Phys. 77, 085901.CrossRefGoogle Scholar
Landahl, M. T. 1980 A note on an algebraic instability of inviscid parallel shear flows. J. Fluid Mech. 98, 243–251.CrossRefGoogle Scholar
Luchini, P. & Bottaro, A. 2014 Adjoint equations in stability analysis. Annu. Rev. Fluid Mech. 46, 493–517.CrossRefGoogle Scholar
Monokrousos, A., Bottaro, A., Brandt, L., Di Vita, A. & Henningson, D. S. 2011 Nonequilibrium thermodynamics and the optimal path to turbulence in shear flows. Phys. Rev. Lett. 106, 134502.CrossRefGoogle ScholarPubMed
Olvera, D. & Kerswell, R. R. 2014 Coherent structures in stratified plane Couette flows. Bull. Am. Phys. Soc. 59 (20), 255.Google Scholar
Orr, W. M. 1907 The stability or instability of the steady motions of a perfect liquid and of a viscous liquid. Part I. A perfect liquid. Proc. R. Irish Acad. A 27, 9–68.Google Scholar
Pringle, C. C. T. & Kerswell, R. R. 2010 Using nonlinear transient growth to construct the minimal seed for shear flow turbulence. Phys. Rev. Lett. 105, 154502.CrossRefGoogle ScholarPubMed
Pringle, C. C. T., Willis, A. P. & Kerswell, R. R. 2012 Minimal seeds for shear flow turbulence: using nonlinear transient growth to touch the edge of chaos. J. Fluid Mech. 702, 415–443.CrossRefGoogle Scholar
Rabin, S. M. E., Caulfield, C. P. & Kerswell, R. R. 2012 Triggering turbulence efficiently in plane Couette flow. J. Fluid Mech. 712, 244–272.CrossRefGoogle Scholar
Schmid, P. J. 2007 Nonmodal stability theory. Annu. Rev. Fluid Mech. 39, 129–162.CrossRefGoogle Scholar
Taylor, J. R.2008 Numerical simulations of the stratified oceanic bottom boundary layer. PhD thesis, Mechanical Engineering, University of California, San Diego. Unpublished.Google Scholar
Waleffe, F. 1997 On a self-sustaining process in shear flows. Phys. Fluids 9, 883–900.CrossRefGoogle Scholar
Waleffe, F. 2001 Exact coherent structures in channel flow. J. Fluid Mech. 435, 93–102.CrossRefGoogle Scholar
Wedin, H. & Kerswell, R. R. 2004 Exact coherent structures in pipe flow: travelling wave solutions. J. Fluid Mech. 508, 333–371.CrossRefGoogle Scholar

Eaves and Caulfield supplementary movie

Evolution in time of the isosurfaces of streamwise velocity u = 0.6 max(u) (blue) and u = -0.6 max(u) (red) for the minimal seed trajectories in the narrow geometry N. RiB= 0 (top left), 10-4 (top middle), 10-3(top right), 3x10-3 (bottom left) and 10-2 (bottom middle). Counter in the bottom right corner shows time in advective units.

Download Eaves and Caulfield supplementary movie(Video)
Video 10.3 MB

Eaves and Caulfield supplementary movie

Evolution in time of the isosurfaces of streamwise velocity u = 0.6 max(u) (blue) and u = -0.6 max(u) (red) for the minimal seed trajectories in the narrow geometry N. RiB= 0 (top left), 10-4 (top middle), 10-3(top right), 3x10-3 (bottom left) and 10-2 (bottom middle). Counter in the bottom right corner shows time in advective units.

Download Eaves and Caulfield supplementary movie(Video)
Video 14.7 MB

Eaves and Caulfield supplementary movie

Evolution in time of the isosurfaces of streamwise velocity u = 0.6 max(u) (blue) and u = -0.6 max(u) (red) for the minimal seed trajectories in the wide geometry W. RiB = 0 (top left), 3x10-3 (top right) and 10-2(bottom left). Counter in the bottom right corner shows time in advective units.

Download Eaves and Caulfield supplementary movie(Video)
Video 6.7 MB

Eaves and Caulfield supplementary movie

Evolution in time of the isosurfaces of streamwise velocity u = 0.6 max(u) (blue) and u = -0.6 max(u) (red) for the minimal seed trajectories in the wide geometry W. RiB = 0 (top left), 3x10-3 (top right) and 10-2(bottom left). Counter in the bottom right corner shows time in advective units.

Download Eaves and Caulfield supplementary movie(Video)
Video 7.2 MB