A theoretical study of the decay of plane gaseous detonations is presented. The analysis concerns the relaxation of weakly overdriven detonations toward the Chapman–Jouguet (CJ) regime when the supporting piston is suddenly arrested. The initial condition concerns propagation velocities 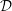${\mathcal{D}}$ that are not far from that of the CJ wave 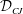${\mathcal{D}}_{CJ}$, 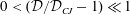$0<({\mathcal{D}}/{\mathcal{D}}_{CJ}-1)\ll 1$. The unsteady inner structure of the detonation wave is taken into account analytically for small heat release, i.e. when the propagation Mach number of the CJ wave 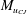$M_{u_{CJ}}$ is small, 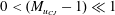$0<(M_{u_{CJ}}-1)\ll 1$. Under such conditions the flow is transonic across the inner structure. Then, with small differences between heat capacities (Newtonian limit), the problem reduces to an integral equation for the velocity of the lead shock. This equation governs the detonation dynamics resulting from the coupling of the unsteady inner structure with the self-similar dynamics of the centred rarefaction wave in the burnt gas. The key point of the asymptotic analysis is that the response time of the inner structure is larger than the reaction time. How, and to what extent, the result is relevant for real detonations is discussed in the text. In a preliminary step the steady-state approximation is revisited with particular attention paid to the location of the sonic condition.