Hostname: page-component-8448b6f56d-sxzjt Total loading time: 0 Render date: 2024-04-23T08:02:18.176Z Has data issue: false hasContentIssue false
  • English
  • Français

Critical transitions in thin layer turbulence

Published online by Cambridge University Press:  01 June 2017

Santiago Jose Benavides  and
Alexandros Alexakis Open the ORCID record for Alexandros Alexakis [Opens in a new window]
Santiago Jose Benavides
Affiliation:
Department of Earth, Atmospheric and Planetary Sciences, Massachusetts Institute of Technology, 77 Massachusetts Ave., Cambridge, MA 02139-4307, USA
Alexandros Alexakis*
Affiliation:
Laboratoire de Physique Statistique, École Normale Supérieure, CNRS, Université Pierre et Marie Curie, Université Paris Diderot, Paris 75005, France
*
†Email address for correspondence: alexakis@lps.ens.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate a model of thin layer turbulence that follows the evolution of the two-dimensional motions 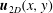$\boldsymbol{u}_{2D}(x,y)$ along the horizontal directions 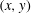$(x,y)$ coupled to a single Fourier mode along the vertical direction ( $z$ ) of the form 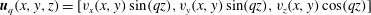$\boldsymbol{u}_{q}(x,y,z)=[v_{x}(x,y)\sin (qz),v_{y}(x,y)\sin (qz),v_{z}(x,y)\cos (qz)]$ , reducing thus the system to two coupled, two-dimensional equations. The model, despite its simplicity and ad hoc construction, displays a rich behaviour. Its reduced dimensionality allows a thorough investigation of the transition from a forward to an inverse cascade of energy as the thickness of the layer 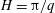$H=\unicode[STIX]{x03C0}/q$ is varied. Starting from a thick layer and reducing its thickness it is shown that two critical heights are met: (i) one for which the forward unidirectional cascade (similar to three-dimensional turbulence) transitions to a bidirectional cascade transferring energy to both small and large scales and (ii) one for which the bidirectional cascade transitions to a unidirectional inverse cascade when the layer becomes very thin (similar to two-dimensional turbulence). The two critical heights are shown to have different properties close to criticality that we are able to analyse with numerical simulations for a wide range of Reynolds numbers and aspect ratios.

JFM classification

Geophysical and Geological Flows: Atmospheric flows Turbulent Flows: Turbulent Flows Turbulent Flows: Turbulent transition
Type
Papers
Information
Journal of Fluid Mechanics , Volume 822 , 10 July 2017 , pp. 364 - 385
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alexakis, A. 2011 Two-dimensional behavior of three-dimensional magnetohydrodynamic flow with a strong guiding field. Phys. Rev. E 84 (5), 056330.Google Scholar
Alexakis, A. & Doering, C. R. 2006 Energy and enstrophy dissipation in steady state 2d turbulence. Phys. Lett. A 359 (6), 652–657.CrossRefGoogle Scholar
Alexakis, A. & Ponty, Y. 2008 Effect of the Lorentz force on on–off dynamo intermittency. Phys. Rev. E 77 (5), 056308.Google ScholarPubMed
Barkley, D., Song, B., Mukund, V., Lemoult, G., Avila, M. & Hof, B. 2015 The rise of fully turbulent flow. Nature 526 (7574), 550–553.CrossRefGoogle ScholarPubMed
Boffetta, G. & Ecke, R. E. 2012 Two-dimensional turbulence. Annu. Rev. Fluid Mech. 44, 427–451.Google Scholar
Boffetta, G. & Musacchio, S. 2010 Evidence for the double cascade scenario in two-dimensional turbulence. Phys. Rev. E 82 (1), 016307.Google Scholar
Byrne, D., Xia, H. & Shats, M. 2011 Robust inverse energy cascade and turbulence structure in three-dimensional layers of fluid. Phys. Fluids 23 (9), 095109.CrossRefGoogle Scholar
Byrne, D. & Zhang, J. A. 2013 Height-dependent transition from 3-D to 2-D turbulence in the hurricane boundary layer. Geophys. Rev. Lett. 40, 1439–1442.Google Scholar
Campagne, A., Gallet, B., Moisy, F. & Cortet, P.-P. 2014 Direct and inverse energy cascades in a forced rotating turbulence experiment. Phys. Fluids 26 (12), 125112.CrossRefGoogle Scholar
Celani, A., Musacchio, S. & Vincenzi, D. 2010 Turbulence in more than two and less than three dimensions. Phys. Rev. Lett. 104 (18), 184506.CrossRefGoogle ScholarPubMed
Chen, S., Ecke, R. E., Eyink, G. L., Rivera, M., Wan, M. & Xiao, Z. 2006 Physical mechanism of the two-dimensional inverse energy cascade. Phys. Rev. Lett. 96 (8), 084502.CrossRefGoogle ScholarPubMed
Chertkov, M., Connaughton, C., Kolokolov, I. & Lebedev, V. 2007 Dynamics of energy condensation in two-dimensional turbulence. Phys. Rev. Lett. 99 (8), 084501.Google Scholar
Deusebio, E., Boffetta, G., Lindborg, E. & Musacchio, S. 2014 Dimensional transition in rotating turbulence. Phys. Rev. E 90 (2), 023005.Google Scholar
Diamond, P. H., Itoh, S.-I., Itoh, K. & Hahm, T. S. 2005 TOPICAL REVIEW: zonal flows in plasma. Plasma Phys. Control. Fusion 47, R35–R161.Google Scholar
Eyink, G. L. 1996 Exact results on stationary turbulence in 2d: consequences of vorticity conservation. Physica D 91 (1–2), 97–142.Google Scholar
Eyink, G. L. 2006 Multi-scale gradient expansion of the turbulent stress tensor. J. Fluid Mech. 549, 159–190.CrossRefGoogle Scholar
Frisch, U. 1995 Turbulence: The Legacy of A. N. Kolmogorov. Cambridge University Press.CrossRefGoogle Scholar
Fujisaka, H., Ishii, H., Inoue, M. & Yamada, T. 1986 Intermittency caused by chaotic modulation. II – Lyapunov exponent, fractal structure and power spectrum. Progr. Theoret. Phys. 76, 1198–1209.Google Scholar
Gallet, B. & Doering, C. R. 2015 Exact two-dimensionalization of low-magnetic-Reynolds-number flows subject to a strong magnetic field. J. Fluid Mech. 773, 154–177.Google Scholar
Goldenfeld, N. & Shih, H.-Y. 2017 Turbulence as a problem in non-equilibrium statistical mechanics. J. Stat. Phys. 167, 575–594.Google Scholar
Gomez, D. O., Mininni, P. D. & Dmitruk, P. 2005 Parallel simulations in turbulent MHD. Phys. Scr. T116, 123–127.CrossRefGoogle Scholar
Grinstein, G., Munoz, M. A. & Tu, Y. 1996 Phase structure of systems with multiplicative noise. Phys. Rev. Lett. 76 (23), 4376.Google Scholar
Hammer, P. W., Platt, N., Hammel, S. M., Heagy, J. F. & Lee, B. D. 1994 Experimental observation of on–off intermittency. Phys. Rev. Lett. 73 (8), 1095.Google Scholar
Horsthemke, W. & Lefever, R. 2006 Noise-Induced Transitions. Springer.Google Scholar
Izakov, M. N. 2013 Large-scale quasi-two-dimensional turbulence and a inverse spectral flux of energy in the atmosphere of Venus. Solar System Res. 47, 170–181.Google Scholar
John, T., Stannarius, R. & Behn, U. 1999 On–off intermittency in stochastically driven electrohydrodynamic convection in nematics. Phys. Rev. Lett. 83 (4), 749.CrossRefGoogle Scholar
Laurie, J., Boffetta, G., Falkovich, G., Kolokolov, I. & Lebedev, V. 2014 Universal profile of the vortex condensate in two-dimensional turbulence. Phys. Rev. Lett. 113 (25), 254503.CrossRefGoogle ScholarPubMed
Lemoult, G., Shi, L., Avila, K., Jalikop, S. V., Avila, M. & Hof, B. 2016 Directed percolation phase transition to sustained turbulence in Couette flow. Nat. Phys 12, 254–258.Google Scholar
Lesur, G. & Longaretti, P.-Y. 2011 Non-linear energy transfers in accretion discs MRI turbulence. I. Net vertical field case. Astron. Astrophys. 528, A17.Google Scholar
Marino, R., Mininni, P. D., Rosenberg, D. & Pouquet, A. 2013 Inverse cascades in rotating stratified turbulence: fast growth of large scales. Europhys. Lett. 102, 44006.CrossRefGoogle Scholar
Marino, R., Pouquet, A. & Rosenberg, D. 2015 Resolving the paradox of oceanic large-scale balance and small-scale mixing. Phys. Rev. Lett. 114 (11), 114504.Google Scholar
Obukhov, S. P. 1980 The problem of directed percolation. Physica A 101 (1), 145–155.Google Scholar
Platt, N., Spiegel, E. A. & Tresser, C. 1993 On–off intermittency – A mechanism for bursting. Phys. Rev. Lett. 70, 279–282.CrossRefGoogle ScholarPubMed
Pomeau, Y. 1986 Front motion, metastability and subcritical bifurcations in hydrodynamics. Phys. D 23, 3–11.Google Scholar
Pouquet, A. & Marino, R. 2013 Geophysical turbulence and the duality of the energy flow across scales. Phys. Rev. Lett. 111 (23), 234501.Google Scholar
Rödelsperger, F., Čenys, A. & Benner, H. 1995 On–off intermittency in spin-wave instabilities. Phys. Rev. Lett. 75 (13), 2594.Google Scholar
Rosenberg, D., Pouquet, A., Marino, R. & Mininni, P. D. 2015 Evidence for Bolgiano-Obukhov scaling in rotating stratified turbulence using high-resolution direct numerical simulations. Phys. Fluids 27 (5), 055105.Google Scholar
Sano, M. & Tamai, K. 2016 A universal transition to turbulence in channel flow. Nat. Phys 12, 249–253.Google Scholar
Sen, A., Mininni, P. D., Rosenberg, D. & Pouquet, A. 2012 Anisotropy and nonuniversality in scaling laws of the large-scale energy spectrum in rotating turbulence. Phys. Rev. E 86 (3), 036319.Google Scholar
Seshasayanan, K. & Alexakis, A. 2016 Critical behavior in the inverse to forward energy transition in two-dimensional magnetohydrodynamic flow. Phys. Rev. E 93, 013104.Google Scholar
Seshasayanan, K., Benavides, S. J. & Alexakis, A. 2014 On the edge of an inverse cascade. Phys. Rev. E 90, 051003.Google Scholar
Shats, M., Byrne, D. & Xia, H. 2010 Turbulence decay rate as a measure of flow dimensionality. Phys. Rev. Lett. 105 (26), 264501.Google Scholar
Smith, L. M., Chasnov, J. R. & Waleffe, F. 1996 Crossover from two-to three-dimensional turbulence. Phys. Rev. Lett. 77 (12), 2467.Google Scholar
Smith, L. M. & Waleffe, F. 1999 Transfer of energy to two-dimensional large scales in forced, rotating three-dimensional turbulence. Phys. Fluids 11, 1608–1622.Google Scholar
Sozza, A., Boffetta, G., Muratore-Ginanneschi, P. & Musacchio, S. 2015 Dimensional transition of energy cascades in stably stratified forced thin fluid layers. Phys. Fluids 27 (3), 035112.Google Scholar
Xia, H., Byrne, D., Falkovich, G. & Shats, M. 2011 Upscale energy transfer in thick turbulent fluid layers. Nat. Phys. 7, 321–324.CrossRefGoogle Scholar
Xiao, Z., Wan, M., Chen, S. & Eyink, G. L. 2009 Physical mechanism of the inverse energy cascade of two-dimensional turbulence: a numerical investigation. J. Fluid Mech. 619, 1–44.CrossRefGoogle Scholar
Yarom, E., Vardi, Y. & Sharon, E. 2013 Experimental quantification of inverse energy cascade in deep rotating turbulence. Phys. Fluids 25 (8), 085105.CrossRefGoogle Scholar