Article contents
Critical layer and radiative instabilities in shallow-water shear flows
Published online by Cambridge University Press: 23 June 2014
Abstract
In this study a linear stability analysis of shallow-water flows is undertaken for a representative Froude number 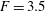 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}F=3.5$. The focus is on monotonic base flow profiles
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}F=3.5$. The focus is on monotonic base flow profiles 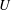 $U$ without an inflection point, in order to study critical layer instability (CLI) and its interaction with radiative instability (RI). First the dispersion relation is presented for the piecewise linear profile studied numerically by Satomura (J. Meterol. Soc. Japan, vol. 59, 1981, pp. 148–167) and using WKBJ analysis an interpretation given of mode branches, resonances and radiative instability. In particular surface gravity (SG) waves can resonate with a limit mode (LM) (or Rayleigh wave), localised near the discontinuity in shear in the flow; in this piecewise profile there is no critical layer. The piecewise linear profile is then continuously modified in a family of nonlinear profiles, to show the effect of the vorticity gradient
$U$ without an inflection point, in order to study critical layer instability (CLI) and its interaction with radiative instability (RI). First the dispersion relation is presented for the piecewise linear profile studied numerically by Satomura (J. Meterol. Soc. Japan, vol. 59, 1981, pp. 148–167) and using WKBJ analysis an interpretation given of mode branches, resonances and radiative instability. In particular surface gravity (SG) waves can resonate with a limit mode (LM) (or Rayleigh wave), localised near the discontinuity in shear in the flow; in this piecewise profile there is no critical layer. The piecewise linear profile is then continuously modified in a family of nonlinear profiles, to show the effect of the vorticity gradient  $Q^{\prime } = - U^{\prime \prime }$ on the nature of the modes. Some modes remain as modes and others turn into quasi-modes (QM), linked to Landau damping of disturbances to the flow, depending on the sign of the vorticity gradient at the critical point. Thus an interpretation of critical layer instability for continuous profiles is given, as the remnant of the resonance with the LM. Numerical results and WKBJ analysis of critical layer instability and radiative instability for more general smooth profiles are provided. A link is made between growth rate formulae obtained by considering wave momentum and those found via the WKBJ approximation. Finally the competition between the stabilising effect of vorticity gradients in a critical layer and the destabilising effect of radiation (radiative instability) is studied.
$Q^{\prime } = - U^{\prime \prime }$ on the nature of the modes. Some modes remain as modes and others turn into quasi-modes (QM), linked to Landau damping of disturbances to the flow, depending on the sign of the vorticity gradient at the critical point. Thus an interpretation of critical layer instability for continuous profiles is given, as the remnant of the resonance with the LM. Numerical results and WKBJ analysis of critical layer instability and radiative instability for more general smooth profiles are provided. A link is made between growth rate formulae obtained by considering wave momentum and those found via the WKBJ approximation. Finally the competition between the stabilising effect of vorticity gradients in a critical layer and the destabilising effect of radiation (radiative instability) is studied.
- Type
- Papers
- Information
- Copyright
- © 2014 Cambridge University Press
References
- 6
- Cited by


