1 Introduction
The repeated fascination of fluid dynamists to study drops in various situations often comes about because this apparently simple system behaves as a model oscillator. The balance between fluid inertia and surface tension that tends to restore the surface of minimal energy, yields
 $f\simeq (\unicode[STIX]{x1D6FE}/\unicode[STIX]{x1D70C}R^{3})^{1/2}$
as a natural frequency for the oscillations, where
$f\simeq (\unicode[STIX]{x1D6FE}/\unicode[STIX]{x1D70C}R^{3})^{1/2}$
as a natural frequency for the oscillations, where
 $\unicode[STIX]{x1D6FE}$
and
$\unicode[STIX]{x1D6FE}$
and
 $\unicode[STIX]{x1D70C}$
are the surface tension and density of the fluid and
$\unicode[STIX]{x1D70C}$
are the surface tension and density of the fluid and
 $R$
is the drop radius. However, liquid–substrate friction often dramatically attenuates the dynamics. Still, there exist situations where friction with the substrate vanishes, making the liquid drop very mobile, for instance when a thin air cushion intercalated in between keeps the drop in levitation.
$R$
is the drop radius. However, liquid–substrate friction often dramatically attenuates the dynamics. Still, there exist situations where friction with the substrate vanishes, making the liquid drop very mobile, for instance when a thin air cushion intercalated in between keeps the drop in levitation.
The Leidenfrost effect (Leidenfrost Reference Leidenfrost1756) provides a situation of very weak friction, and has been the subject of numerous studies with both fundamental and applied scopes (Quéré Reference Quéré2013). In metallurgy, one tries to avoid it, as it is detrimental for a sharp quench in temperature, which is required for the best mechanical properties, by dramatically limiting heat transfer between the alloy and the surrounding cooling liquid. Conversely, it can be utilised on purpose to move droplets uphill on sloping substrates (Linke et al.
Reference Linke2006). In Jules Vernes’ book, Michel Strogoff’s blindness was prevented thanks to this salutary effect, helped by a few tears, after a red-hot sword blade was put on his eyes. Holter & Glasscock (Reference Holter and Glasscock1952) were the first to report spontaneous oscillations of star-shaped drops, and opportunely published it in a journal of acoustics. Others later investigated these oscillations (Adachi & Takaki Reference Adachi and Takaki1984) and questioned their origin. A Marangoni effect due to a temperature gradient developing between the centre and the periphery of the drop was proposed (Tokugawa & Takaki Reference Tokugawa and Takaki1994). On the other hand, Brunet & Snoeijer (Reference Brunet and Snoeijer2011) and Bouwhuis et al. (Reference Bouwhuis, Winkels, Peters, Brunet, van der Meer and Snoeijer2013) reported similar behaviour for a drop sitting on an air cushion blown from below at room temperature, which dismissed the aforementioned mechanism. The star shapes are reminiscent of other situations where drops are driven by external time-periodic fields, e.g. substrate vibrations, acoustic modulation, fluctuating magnetic field (Brunet & Snoeijer Reference Brunet and Snoeijer2011), except that in the levitated drops there is no periodic forcing. Hence a purely hydrodynamic instability was invoked (Bouwhuis et al.
Reference Bouwhuis, Winkels, Peters, Brunet, van der Meer and Snoeijer2013).
Since a perfectly non-wetting drop adopts the shape of a puddle of height
 $h=2l_{c}$
, where
$h=2l_{c}$
, where
 $l_{c}=(\unicode[STIX]{x1D6FE}/\unicode[STIX]{x1D70C}g)^{1/2}$
is the capillary length, when such an instability leads to a time-periodic vertical motion of the drop centre of mass, the effective gravity
$l_{c}=(\unicode[STIX]{x1D6FE}/\unicode[STIX]{x1D70C}g)^{1/2}$
is the capillary length, when such an instability leads to a time-periodic vertical motion of the drop centre of mass, the effective gravity
 $g_{eff}$
that the drop feels becomes modulated in time and so do the capillary length and drop height. Because of volume conservation, the drop radius
$g_{eff}$
that the drop feels becomes modulated in time and so do the capillary length and drop height. Because of volume conservation, the drop radius
 $R$
is also subjected to this modulation. Hence, given the general expression of the drop eigenfrequency
$R$
is also subjected to this modulation. Hence, given the general expression of the drop eigenfrequency
 $f$
stated above, it becomes clear that drop oscillations are induced by a parametric forcing. But the underlying mechanism of the instability remains ill-understood, as shown by several seemingly contradictory results on the dependence of frequency on drop radius (Bouwhuis et al.
Reference Bouwhuis, Winkels, Peters, Brunet, van der Meer and Snoeijer2013; Caswell Reference Caswell2014; Ma, Lietor-Santos & Burton Reference Ma, Lietor-Santos and Burton2017).
$f$
stated above, it becomes clear that drop oscillations are induced by a parametric forcing. But the underlying mechanism of the instability remains ill-understood, as shown by several seemingly contradictory results on the dependence of frequency on drop radius (Bouwhuis et al.
Reference Bouwhuis, Winkels, Peters, Brunet, van der Meer and Snoeijer2013; Caswell Reference Caswell2014; Ma, Lietor-Santos & Burton Reference Ma, Lietor-Santos and Burton2017).
2 Overview
Ma & Burton (Reference Ma and Burton2018) present exhaustive experiments with six different fluids and a large range of temperatures and drop volumes. Thanks to the slight curvature of the substrate, they could keep stable large drops (
 $R>4l_{c}$
) that otherwise would have broken under the action of a growing bubble of vapour below (Snoeijer, Brunet & Eggers Reference Snoeijer, Brunet and Eggers2009); hence they observed vibrating drops with wavenumber
$R>4l_{c}$
) that otherwise would have broken under the action of a growing bubble of vapour below (Snoeijer, Brunet & Eggers Reference Snoeijer, Brunet and Eggers2009); hence they observed vibrating drops with wavenumber
 $n$
from 2 to 13, and
$n$
from 2 to 13, and
 $R$
up to 2.4 cm. Furthermore, they measured the pressure underneath the drop, and found that the appearance of the instability goes hand in hand with pressure fluctuations, of typical frequency
$R$
up to 2.4 cm. Furthermore, they measured the pressure underneath the drop, and found that the appearance of the instability goes hand in hand with pressure fluctuations, of typical frequency
 $f_{p}$
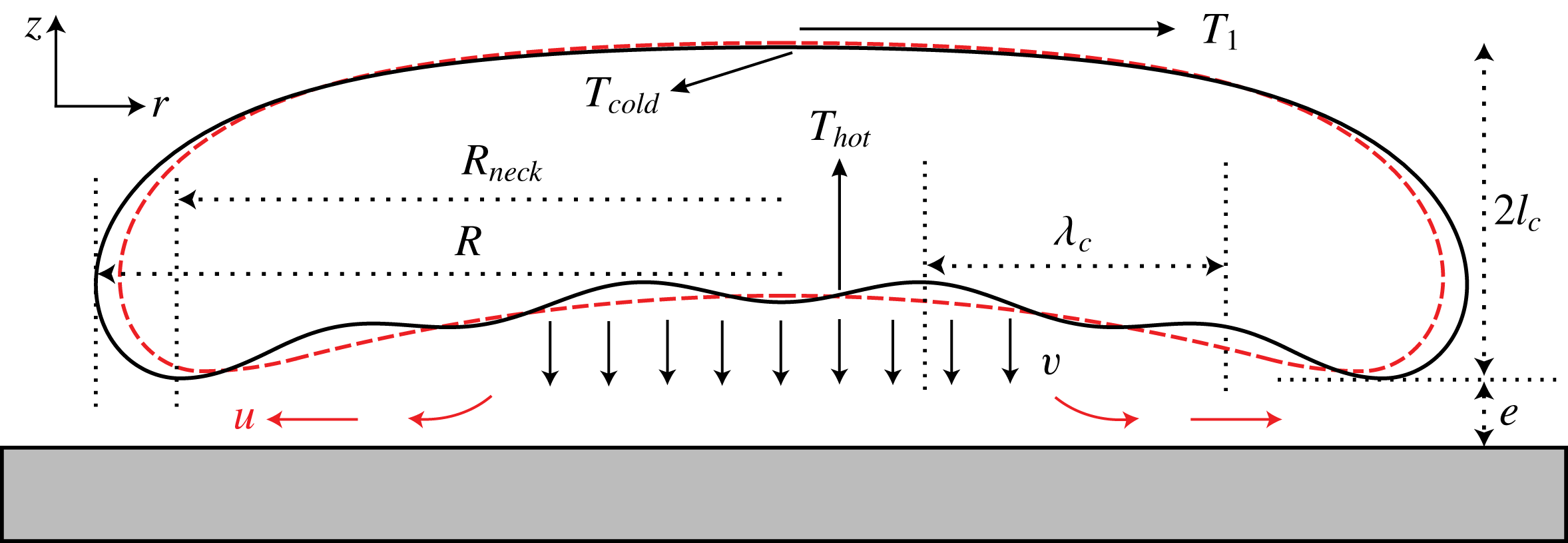
. Also, they used a smart visualisation technique that evidenced capillary waves not only on top and at the edge of the drop, but also underneath. A sketch of their system is depicted in figure 1. One of their most striking results is the independence of
$f_{p}$
. Also, they used a smart visualisation technique that evidenced capillary waves not only on top and at the edge of the drop, but also underneath. A sketch of their system is depicted in figure 1. One of their most striking results is the independence of
 $f_{p}$
(and so of the frequency of the drop oscillations
$f_{p}$
(and so of the frequency of the drop oscillations
 $f_{d}$
) and azimuthal wavelength
$f_{d}$
) and azimuthal wavelength
 $\unicode[STIX]{x1D706}_{d}$
on the drop radius. They found that
$\unicode[STIX]{x1D706}_{d}$
on the drop radius. They found that
 $f_{d}$
is dependent only on
$f_{d}$
is dependent only on
 $l_{c}$
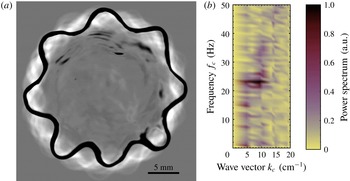
, which is dependent only on liquid properties. Figure 2(a) shows an oscillating drop from below, where both the external corrugation and capillary waves below are visible. Figure 2(b) is the corresponding power spectrum that evidences the selection of frequency for these waves. The wavenumber
$l_{c}$
, which is dependent only on liquid properties. Figure 2(a) shows an oscillating drop from below, where both the external corrugation and capillary waves below are visible. Figure 2(b) is the corresponding power spectrum that evidences the selection of frequency for these waves. The wavenumber
 $n$
self-adapts and is found to increase linearly with the radius,
$n$
self-adapts and is found to increase linearly with the radius,
 $n\sim R$
.
$n\sim R$
.
Figure 1. The overall sketch of the drop levitating on its own vapour underneath.
Figure 2. (a) A star-shaped drop of acetone levitating on its own vapour, viewed from below, and the radial capillary waves underneath. (b) The corresponding power spectrum in frequency and wavenumber.
These results seem in sharp disagreement with previous ones which showed a significant dependence of
 $f_{d}$
on
$f_{d}$
on
 $R$
(Adachi & Takaki Reference Adachi and Takaki1984; Bouwhuis et al.
Reference Bouwhuis, Winkels, Peters, Brunet, van der Meer and Snoeijer2013; Caswell Reference Caswell2014). However, the latter studies examined the situation of smaller droplets (
$R$
(Adachi & Takaki Reference Adachi and Takaki1984; Bouwhuis et al.
Reference Bouwhuis, Winkels, Peters, Brunet, van der Meer and Snoeijer2013; Caswell Reference Caswell2014). However, the latter studies examined the situation of smaller droplets (
 $R<4l_{c}$
), for which Ma & Burton explain the dependence on
$R<4l_{c}$
), for which Ma & Burton explain the dependence on
 $R$
with an analytical approach.
$R$
with an analytical approach.
Ma & Burton’s measurements and analysis of air flow suggest that the selection on
 $f_{p}$
(and then on
$f_{p}$
(and then on
 $f_{d}$
and
$f_{d}$
and
 $\unicode[STIX]{x1D706}_{d}$
) originates from gravity–capillary waves provoked by the shear stress exerted on the vapour–liquid interface, which explains why oscillations appear above a threshold in temperature or in air flow. This analysis also reconciles the different measurements obtained for small drops and large puddles. These waves cannot develop under too small drops, as their wavelength
$\unicode[STIX]{x1D706}_{d}$
) originates from gravity–capillary waves provoked by the shear stress exerted on the vapour–liquid interface, which explains why oscillations appear above a threshold in temperature or in air flow. This analysis also reconciles the different measurements obtained for small drops and large puddles. These waves cannot develop under too small drops, as their wavelength
 $\unicode[STIX]{x1D706}_{c}\simeq 3.03l_{c}$
would then be larger than
$\unicode[STIX]{x1D706}_{c}\simeq 3.03l_{c}$
would then be larger than
 $R$
. Instead, the profile underneath takes the shape of a bubble with a ‘nip’, i.e. a region of minimal air thickness, where most of the viscous stress responsible for lubrication-induced levitation takes place (Snoeijer et al.
Reference Snoeijer, Brunet and Eggers2009). The radius
$R$
. Instead, the profile underneath takes the shape of a bubble with a ‘nip’, i.e. a region of minimal air thickness, where most of the viscous stress responsible for lubrication-induced levitation takes place (Snoeijer et al.
Reference Snoeijer, Brunet and Eggers2009). The radius
 $R$
remains the only length scale in the radial direction, and the selection of
$R$
remains the only length scale in the radial direction, and the selection of
 $f_{p}$
is set by
$f_{p}$
is set by
 $R$
. Conversely the air layer under large puddles on curved substrates can exhibit several of these minima (see figure 2 in Ma & Burton Reference Ma and Burton2018), with
$R$
. Conversely the air layer under large puddles on curved substrates can exhibit several of these minima (see figure 2 in Ma & Burton Reference Ma and Burton2018), with
 $\unicode[STIX]{x1D706}_{c}$
being the distance between them. Therefore,
$\unicode[STIX]{x1D706}_{c}$
being the distance between them. Therefore,
 $\unicode[STIX]{x1D706}_{c}$
becomes the radial length scale selected by the hydrodynamics, which sets the selection of
$\unicode[STIX]{x1D706}_{c}$
becomes the radial length scale selected by the hydrodynamics, which sets the selection of
 $f_{p}$
independently of
$f_{p}$
independently of
 $R$
. It is insightful to revisit previous measurements in light of Ma & Burton’s, as one sees more clearly that the power-law decrease of
$R$
. It is insightful to revisit previous measurements in light of Ma & Burton’s, as one sees more clearly that the power-law decrease of
 $f_{d}$
with
$f_{d}$
with
 $R$
holds only for
$R$
holds only for
 $R$
smaller than
$R$
smaller than
 $2l_{c}$
(roughly 5 mm for water) (Adachi & Takaki Reference Adachi and Takaki1984; Bouwhuis et al.
Reference Bouwhuis, Winkels, Peters, Brunet, van der Meer and Snoeijer2013), while
$2l_{c}$
(roughly 5 mm for water) (Adachi & Takaki Reference Adachi and Takaki1984; Bouwhuis et al.
Reference Bouwhuis, Winkels, Peters, Brunet, van der Meer and Snoeijer2013), while
 $f_{d}$
seems to reach a plateau for larger
$f_{d}$
seems to reach a plateau for larger
 $R$
.
$R$
.
Overall, with systematic and exhaustive measurements, Ma & Burton unveil the complex hydrodynamical mechanism and frequency selection process that lead to vibrating Leidenfrost star drops. Not only do their measurements with large puddles complete the previous ones, but their analysis explains the selection of frequency over the whole range of drop size.
3 Future
Remaining questions first concern the selection of
 $f_{p}$
and how its mechanism should hold under different conditions. For instance, it would be interesting to check how an undulated substrate, with period ranging between
$f_{p}$
and how its mechanism should hold under different conditions. For instance, it would be interesting to check how an undulated substrate, with period ranging between
 $l_{c}$
and
$l_{c}$
and
 $\unicode[STIX]{x1D706}_{c}$
, could trigger or hinder oscillations and modify the selected
$\unicode[STIX]{x1D706}_{c}$
, could trigger or hinder oscillations and modify the selected
 $f_{p}$
. Another possibility would be to address these questions under different conditions, like drops sandwiched in a Hele-Shaw cell (Celestini et al.
Reference Celestini, Frisch, Cohen, Raufaste, Duchemin and Pomeau2014).
$f_{p}$
. Another possibility would be to address these questions under different conditions, like drops sandwiched in a Hele-Shaw cell (Celestini et al.
Reference Celestini, Frisch, Cohen, Raufaste, Duchemin and Pomeau2014).
Finally, one can wonder whether or not these oscillations could be converted into audible sound waves (
 $f_{p}$
higher than 50 Hz), if higher harmonics appear or even if the fundamental has a high enough frequency, as in Celestini et al. (Reference Celestini, Frisch, Cohen, Raufaste, Duchemin and Pomeau2014). Incidentally, the analogy between these drops and some musical instruments is especially striking. Think of a wind instrument with a vibrating reed, such as a clarinet (Wolfe Reference Wolve2018). Depending on how strongly the performer blows, and on the length of the pipe, either the eigenmode of the reed is excited (a so-called ‘burn note’ generally unsuitable in a musical performance) or the selected sound is due to the vibration of the air column in the pipe (Helmholtz resonator), which couples to the reed vibrations and makes a nice and controlled sound. The levitating drops, depending on their size, are also susceptible to excite vibration modes that are either intrinsic to their size or are tuned by the capillary length intrinsic to the liquid.
$f_{p}$
higher than 50 Hz), if higher harmonics appear or even if the fundamental has a high enough frequency, as in Celestini et al. (Reference Celestini, Frisch, Cohen, Raufaste, Duchemin and Pomeau2014). Incidentally, the analogy between these drops and some musical instruments is especially striking. Think of a wind instrument with a vibrating reed, such as a clarinet (Wolfe Reference Wolve2018). Depending on how strongly the performer blows, and on the length of the pipe, either the eigenmode of the reed is excited (a so-called ‘burn note’ generally unsuitable in a musical performance) or the selected sound is due to the vibration of the air column in the pipe (Helmholtz resonator), which couples to the reed vibrations and makes a nice and controlled sound. The levitating drops, depending on their size, are also susceptible to excite vibration modes that are either intrinsic to their size or are tuned by the capillary length intrinsic to the liquid.




1 Introduction
The repeated fascination of fluid dynamists to study drops in various situations often comes about because this apparently simple system behaves as a model oscillator. The balance between fluid inertia and surface tension that tends to restore the surface of minimal energy, yields $f\simeq (\unicode[STIX]{x1D6FE}/\unicode[STIX]{x1D70C}R^{3})^{1/2}$
as a natural frequency for the oscillations, where
$f\simeq (\unicode[STIX]{x1D6FE}/\unicode[STIX]{x1D70C}R^{3})^{1/2}$
as a natural frequency for the oscillations, where
 $\unicode[STIX]{x1D6FE}$
and
$\unicode[STIX]{x1D6FE}$
and
 $\unicode[STIX]{x1D70C}$
are the surface tension and density of the fluid and
$\unicode[STIX]{x1D70C}$
are the surface tension and density of the fluid and
 $R$
is the drop radius. However, liquid–substrate friction often dramatically attenuates the dynamics. Still, there exist situations where friction with the substrate vanishes, making the liquid drop very mobile, for instance when a thin air cushion intercalated in between keeps the drop in levitation.
$R$
is the drop radius. However, liquid–substrate friction often dramatically attenuates the dynamics. Still, there exist situations where friction with the substrate vanishes, making the liquid drop very mobile, for instance when a thin air cushion intercalated in between keeps the drop in levitation.
The Leidenfrost effect (Leidenfrost Reference Leidenfrost1756) provides a situation of very weak friction, and has been the subject of numerous studies with both fundamental and applied scopes (Quéré Reference Quéré2013). In metallurgy, one tries to avoid it, as it is detrimental for a sharp quench in temperature, which is required for the best mechanical properties, by dramatically limiting heat transfer between the alloy and the surrounding cooling liquid. Conversely, it can be utilised on purpose to move droplets uphill on sloping substrates (Linke et al. Reference Linke2006). In Jules Vernes’ book, Michel Strogoff’s blindness was prevented thanks to this salutary effect, helped by a few tears, after a red-hot sword blade was put on his eyes. Holter & Glasscock (Reference Holter and Glasscock1952) were the first to report spontaneous oscillations of star-shaped drops, and opportunely published it in a journal of acoustics. Others later investigated these oscillations (Adachi & Takaki Reference Adachi and Takaki1984) and questioned their origin. A Marangoni effect due to a temperature gradient developing between the centre and the periphery of the drop was proposed (Tokugawa & Takaki Reference Tokugawa and Takaki1994). On the other hand, Brunet & Snoeijer (Reference Brunet and Snoeijer2011) and Bouwhuis et al. (Reference Bouwhuis, Winkels, Peters, Brunet, van der Meer and Snoeijer2013) reported similar behaviour for a drop sitting on an air cushion blown from below at room temperature, which dismissed the aforementioned mechanism. The star shapes are reminiscent of other situations where drops are driven by external time-periodic fields, e.g. substrate vibrations, acoustic modulation, fluctuating magnetic field (Brunet & Snoeijer Reference Brunet and Snoeijer2011), except that in the levitated drops there is no periodic forcing. Hence a purely hydrodynamic instability was invoked (Bouwhuis et al. Reference Bouwhuis, Winkels, Peters, Brunet, van der Meer and Snoeijer2013).
Since a perfectly non-wetting drop adopts the shape of a puddle of height $h=2l_{c}$
, where
$h=2l_{c}$
, where
 $l_{c}=(\unicode[STIX]{x1D6FE}/\unicode[STIX]{x1D70C}g)^{1/2}$
is the capillary length, when such an instability leads to a time-periodic vertical motion of the drop centre of mass, the effective gravity
$l_{c}=(\unicode[STIX]{x1D6FE}/\unicode[STIX]{x1D70C}g)^{1/2}$
is the capillary length, when such an instability leads to a time-periodic vertical motion of the drop centre of mass, the effective gravity
 $g_{eff}$
that the drop feels becomes modulated in time and so do the capillary length and drop height. Because of volume conservation, the drop radius
$g_{eff}$
that the drop feels becomes modulated in time and so do the capillary length and drop height. Because of volume conservation, the drop radius
 $R$
is also subjected to this modulation. Hence, given the general expression of the drop eigenfrequency
$R$
is also subjected to this modulation. Hence, given the general expression of the drop eigenfrequency
 $f$
stated above, it becomes clear that drop oscillations are induced by a parametric forcing. But the underlying mechanism of the instability remains ill-understood, as shown by several seemingly contradictory results on the dependence of frequency on drop radius (Bouwhuis et al.
Reference Bouwhuis, Winkels, Peters, Brunet, van der Meer and Snoeijer2013; Caswell Reference Caswell2014; Ma, Lietor-Santos & Burton Reference Ma, Lietor-Santos and Burton2017).
$f$
stated above, it becomes clear that drop oscillations are induced by a parametric forcing. But the underlying mechanism of the instability remains ill-understood, as shown by several seemingly contradictory results on the dependence of frequency on drop radius (Bouwhuis et al.
Reference Bouwhuis, Winkels, Peters, Brunet, van der Meer and Snoeijer2013; Caswell Reference Caswell2014; Ma, Lietor-Santos & Burton Reference Ma, Lietor-Santos and Burton2017).
2 Overview
Ma & Burton (Reference Ma and Burton2018) present exhaustive experiments with six different fluids and a large range of temperatures and drop volumes. Thanks to the slight curvature of the substrate, they could keep stable large drops ( $R>4l_{c}$
) that otherwise would have broken under the action of a growing bubble of vapour below (Snoeijer, Brunet & Eggers Reference Snoeijer, Brunet and Eggers2009); hence they observed vibrating drops with wavenumber
$R>4l_{c}$
) that otherwise would have broken under the action of a growing bubble of vapour below (Snoeijer, Brunet & Eggers Reference Snoeijer, Brunet and Eggers2009); hence they observed vibrating drops with wavenumber
 $n$
from 2 to 13, and
$n$
from 2 to 13, and
 $R$
up to 2.4 cm. Furthermore, they measured the pressure underneath the drop, and found that the appearance of the instability goes hand in hand with pressure fluctuations, of typical frequency
$R$
up to 2.4 cm. Furthermore, they measured the pressure underneath the drop, and found that the appearance of the instability goes hand in hand with pressure fluctuations, of typical frequency
 $f_{p}$
. Also, they used a smart visualisation technique that evidenced capillary waves not only on top and at the edge of the drop, but also underneath. A sketch of their system is depicted in figure 1. One of their most striking results is the independence of
$f_{p}$
. Also, they used a smart visualisation technique that evidenced capillary waves not only on top and at the edge of the drop, but also underneath. A sketch of their system is depicted in figure 1. One of their most striking results is the independence of
 $f_{p}$
(and so of the frequency of the drop oscillations
$f_{p}$
(and so of the frequency of the drop oscillations
 $f_{d}$
) and azimuthal wavelength
$f_{d}$
) and azimuthal wavelength
 $\unicode[STIX]{x1D706}_{d}$
on the drop radius. They found that
$\unicode[STIX]{x1D706}_{d}$
on the drop radius. They found that
 $f_{d}$
is dependent only on
$f_{d}$
is dependent only on
 $l_{c}$
, which is dependent only on liquid properties. Figure 2(a) shows an oscillating drop from below, where both the external corrugation and capillary waves below are visible. Figure 2(b) is the corresponding power spectrum that evidences the selection of frequency for these waves. The wavenumber
$l_{c}$
, which is dependent only on liquid properties. Figure 2(a) shows an oscillating drop from below, where both the external corrugation and capillary waves below are visible. Figure 2(b) is the corresponding power spectrum that evidences the selection of frequency for these waves. The wavenumber
 $n$
self-adapts and is found to increase linearly with the radius,
$n$
self-adapts and is found to increase linearly with the radius,
 $n\sim R$
.
$n\sim R$
.
Figure 1. The overall sketch of the drop levitating on its own vapour underneath.
Figure 2. (a) A star-shaped drop of acetone levitating on its own vapour, viewed from below, and the radial capillary waves underneath. (b) The corresponding power spectrum in frequency and wavenumber.
These results seem in sharp disagreement with previous ones which showed a significant dependence of $f_{d}$
on
$f_{d}$
on
 $R$
(Adachi & Takaki Reference Adachi and Takaki1984; Bouwhuis et al.
Reference Bouwhuis, Winkels, Peters, Brunet, van der Meer and Snoeijer2013; Caswell Reference Caswell2014). However, the latter studies examined the situation of smaller droplets (
$R$
(Adachi & Takaki Reference Adachi and Takaki1984; Bouwhuis et al.
Reference Bouwhuis, Winkels, Peters, Brunet, van der Meer and Snoeijer2013; Caswell Reference Caswell2014). However, the latter studies examined the situation of smaller droplets (
 $R<4l_{c}$
), for which Ma & Burton explain the dependence on
$R<4l_{c}$
), for which Ma & Burton explain the dependence on
 $R$
with an analytical approach.
$R$
with an analytical approach.
Ma & Burton’s measurements and analysis of air flow suggest that the selection on $f_{p}$
(and then on
$f_{p}$
(and then on
 $f_{d}$
and
$f_{d}$
and
 $\unicode[STIX]{x1D706}_{d}$
) originates from gravity–capillary waves provoked by the shear stress exerted on the vapour–liquid interface, which explains why oscillations appear above a threshold in temperature or in air flow. This analysis also reconciles the different measurements obtained for small drops and large puddles. These waves cannot develop under too small drops, as their wavelength
$\unicode[STIX]{x1D706}_{d}$
) originates from gravity–capillary waves provoked by the shear stress exerted on the vapour–liquid interface, which explains why oscillations appear above a threshold in temperature or in air flow. This analysis also reconciles the different measurements obtained for small drops and large puddles. These waves cannot develop under too small drops, as their wavelength
 $\unicode[STIX]{x1D706}_{c}\simeq 3.03l_{c}$
would then be larger than
$\unicode[STIX]{x1D706}_{c}\simeq 3.03l_{c}$
would then be larger than
 $R$
. Instead, the profile underneath takes the shape of a bubble with a ‘nip’, i.e. a region of minimal air thickness, where most of the viscous stress responsible for lubrication-induced levitation takes place (Snoeijer et al.
Reference Snoeijer, Brunet and Eggers2009). The radius
$R$
. Instead, the profile underneath takes the shape of a bubble with a ‘nip’, i.e. a region of minimal air thickness, where most of the viscous stress responsible for lubrication-induced levitation takes place (Snoeijer et al.
Reference Snoeijer, Brunet and Eggers2009). The radius
 $R$
remains the only length scale in the radial direction, and the selection of
$R$
remains the only length scale in the radial direction, and the selection of
 $f_{p}$
is set by
$f_{p}$
is set by
 $R$
. Conversely the air layer under large puddles on curved substrates can exhibit several of these minima (see figure 2 in Ma & Burton Reference Ma and Burton2018), with
$R$
. Conversely the air layer under large puddles on curved substrates can exhibit several of these minima (see figure 2 in Ma & Burton Reference Ma and Burton2018), with
 $\unicode[STIX]{x1D706}_{c}$
being the distance between them. Therefore,
$\unicode[STIX]{x1D706}_{c}$
being the distance between them. Therefore,
 $\unicode[STIX]{x1D706}_{c}$
becomes the radial length scale selected by the hydrodynamics, which sets the selection of
$\unicode[STIX]{x1D706}_{c}$
becomes the radial length scale selected by the hydrodynamics, which sets the selection of
 $f_{p}$
independently of
$f_{p}$
independently of
 $R$
. It is insightful to revisit previous measurements in light of Ma & Burton’s, as one sees more clearly that the power-law decrease of
$R$
. It is insightful to revisit previous measurements in light of Ma & Burton’s, as one sees more clearly that the power-law decrease of
 $f_{d}$
with
$f_{d}$
with
 $R$
holds only for
$R$
holds only for
 $R$
smaller than
$R$
smaller than
 $2l_{c}$
(roughly 5 mm for water) (Adachi & Takaki Reference Adachi and Takaki1984; Bouwhuis et al.
Reference Bouwhuis, Winkels, Peters, Brunet, van der Meer and Snoeijer2013), while
$2l_{c}$
(roughly 5 mm for water) (Adachi & Takaki Reference Adachi and Takaki1984; Bouwhuis et al.
Reference Bouwhuis, Winkels, Peters, Brunet, van der Meer and Snoeijer2013), while
 $f_{d}$
seems to reach a plateau for larger
$f_{d}$
seems to reach a plateau for larger
 $R$
.
$R$
.
Overall, with systematic and exhaustive measurements, Ma & Burton unveil the complex hydrodynamical mechanism and frequency selection process that lead to vibrating Leidenfrost star drops. Not only do their measurements with large puddles complete the previous ones, but their analysis explains the selection of frequency over the whole range of drop size.
3 Future
Remaining questions first concern the selection of $f_{p}$
and how its mechanism should hold under different conditions. For instance, it would be interesting to check how an undulated substrate, with period ranging between
$f_{p}$
and how its mechanism should hold under different conditions. For instance, it would be interesting to check how an undulated substrate, with period ranging between
 $l_{c}$
and
$l_{c}$
and
 $\unicode[STIX]{x1D706}_{c}$
, could trigger or hinder oscillations and modify the selected
$\unicode[STIX]{x1D706}_{c}$
, could trigger or hinder oscillations and modify the selected
 $f_{p}$
. Another possibility would be to address these questions under different conditions, like drops sandwiched in a Hele-Shaw cell (Celestini et al.
Reference Celestini, Frisch, Cohen, Raufaste, Duchemin and Pomeau2014).
$f_{p}$
. Another possibility would be to address these questions under different conditions, like drops sandwiched in a Hele-Shaw cell (Celestini et al.
Reference Celestini, Frisch, Cohen, Raufaste, Duchemin and Pomeau2014).
Finally, one can wonder whether or not these oscillations could be converted into audible sound waves ( $f_{p}$
higher than 50 Hz), if higher harmonics appear or even if the fundamental has a high enough frequency, as in Celestini et al. (Reference Celestini, Frisch, Cohen, Raufaste, Duchemin and Pomeau2014). Incidentally, the analogy between these drops and some musical instruments is especially striking. Think of a wind instrument with a vibrating reed, such as a clarinet (Wolfe Reference Wolve2018). Depending on how strongly the performer blows, and on the length of the pipe, either the eigenmode of the reed is excited (a so-called ‘burn note’ generally unsuitable in a musical performance) or the selected sound is due to the vibration of the air column in the pipe (Helmholtz resonator), which couples to the reed vibrations and makes a nice and controlled sound. The levitating drops, depending on their size, are also susceptible to excite vibration modes that are either intrinsic to their size or are tuned by the capillary length intrinsic to the liquid.
$f_{p}$
higher than 50 Hz), if higher harmonics appear or even if the fundamental has a high enough frequency, as in Celestini et al. (Reference Celestini, Frisch, Cohen, Raufaste, Duchemin and Pomeau2014). Incidentally, the analogy between these drops and some musical instruments is especially striking. Think of a wind instrument with a vibrating reed, such as a clarinet (Wolfe Reference Wolve2018). Depending on how strongly the performer blows, and on the length of the pipe, either the eigenmode of the reed is excited (a so-called ‘burn note’ generally unsuitable in a musical performance) or the selected sound is due to the vibration of the air column in the pipe (Helmholtz resonator), which couples to the reed vibrations and makes a nice and controlled sound. The levitating drops, depending on their size, are also susceptible to excite vibration modes that are either intrinsic to their size or are tuned by the capillary length intrinsic to the liquid.