Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-17T23:36:53.817Z Has data issue: false hasContentIssue false
  • English
  • Français

Collective motion in a suspension of micro-swimmers that run-and-tumble and rotary diffuse

Published online by Cambridge University Press:  28 September 2015

Deepak Krishnamurthy  and
Ganesh Subramanian
Deepak Krishnamurthy
Affiliation:
Engineering Mechanics Unit, Jawaharlal Nehru Centre for Advanced Scientific Research, Jakkur, Bangalore, Karnataka 560064, India
Ganesh Subramanian*
Affiliation:
Engineering Mechanics Unit, Jawaharlal Nehru Centre for Advanced Scientific Research, Jakkur, Bangalore, Karnataka 560064, India
*
†Email address for correspondence: sganesh@jncasr.ac.in
Get access Rights & Permissions [Opens in a new window]

Abstract

Recent experiments have shown that suspensions of swimming micro-organisms are characterized by complex dynamics involving enhanced swimming speeds, large-scale correlated motions and enhanced diffusivities of embedded tracer particles. Understanding this dynamics is of fundamental interest and also has relevance to biological systems. The observed collective dynamics has been interpreted as the onset of a hydrodynamic instability, of the quiescent isotropic state of pushers, swimmers with extensile force dipoles, above a critical threshold proportional to the swimmer concentration. In this work, we develop a particle-based model to simulate a suspension of hydrodynamically interacting rod-like swimmers to estimate this threshold. Unlike earlier simulations, the velocity disturbance field due to each swimmer is specified in terms of the intrinsic swimmer stress alone, as per viscous slender-body theory. This allows for a computationally efficient kinematic simulation where the interaction law between swimmers is known a priori. The neglect of induced stresses is of secondary importance since the aforementioned instability arises solely due to the intrinsic swimmer force dipoles.

Our kinematic simulations include, for the first time, intrinsic decorrelation mechanisms found in bacteria, such as tumbling and rotary diffusion. To begin with, we simulate so-called straight swimmers that lack intrinsic orientation decorrelation mechanisms, and a comparison with earlier results serves as a proof of principle. Next, we simulate suspensions of swimmers that tumble and undergo rotary diffusion, as a function of the swimmer number density 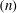$(n)$, and the intrinsic decorrelation time (the average duration between tumbles, ${\it\tau}$, for tumblers, and the inverse of the rotary diffusivity, 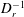$D_{r}^{-1}$, for rotary diffusers). The simulations, as a function of the decorrelation time, are carried out with hydrodynamic interactions (between swimmers) turned off and on, and for both pushers and pullers (swimmers with contractile force dipoles). The ‘interactions-off’ simulations allow for a validation based on analytical expressions for the tracer diffusivity in the stable regime, and reveal a non-trivial box size dependence that arises with varying strength of the hydrodynamic interactions. The ‘interactions-on’ simulations lead us to our main finding: the existence of a box-size-independent parameter that characterizes the onset of instability in a pusher suspension, and is given by 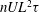$nUL^{2}{\it\tau}$ for tumblers and 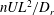$nUL^{2}/D_{r}$ for rotary diffusers; here, 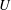$U$ and 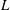$L$ are the swimming speed and swimmer length, respectively. The instability manifests as a bifurcation of the tracer diffusivity curves, in pusher and puller suspensions, for values of the above dimensionless parameters exceeding a critical threshold.

JFM classification

Biological Fluid Dynamics: Biological Fluid Dynamics Instability: Instability Biological Fluid Dynamics: Micro-organism dynamics
Type
Papers
Information
Journal of Fluid Mechanics , Volume 781 , 25 October 2015 , pp. 422 - 466
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

‡

Present address: Department of Mechanical Engineering, Stanford University, Building 530, 440 Escondido Mall, Stanford, CA 94305-3030, USA.

References

Abramowitz, M. & Stegun, I. A. 1972 Handbook of Mathematical Functions: With Formulas, Graphs, and Mathematical Tables. Courier Dover.Google Scholar
Batchelor, G. K. 1970 Slender-body theory for particles of arbitrary cross-section in stokes flow. J. Fluid Mech. 44 (03), 419–440.Google Scholar
Beenakker, C. W. J. 1986 Ewald sum of the rotne–prager tensor. J. Chem. Phys. 85 (3), 1581–1582.Google Scholar
Berg, H. C. 1993 Random Walks in Biology. Princeton University Press.Google Scholar
Berg, H. C. 2004 E. coli in Motion. Springer.Google Scholar
Berg, H. C. & Brown, D. A. 1972 Chemotaxis in Escherichia coli analysed by three-dimensional tracking. Nature 239 (5374), 500–504.Google Scholar
Brady, J. F. & Bossis, G. 1988 Stokesian dynamics. Annu. Rev. Fluid Mech. 20, 111–157.Google Scholar
Brady, J. F., Phillips, R. J., Lester, J. C. & Bossis, G. 1988 Dynamic simulation of hydrodynamically interacting suspensions. J. Fluid Mech. 195, 257–280.Google Scholar
Brennen, C. & Winet, H. 1977 Fluid mechanics of propulsion by cilia and flagella. Annu. Rev. Fluid Mech. 9 (1), 339–398.Google Scholar
Butler, J. E. & Shaqfeh, E. S. G. 2002 Dynamic simulations of the inhomogeneous sedimentation of rigid fibres. J. Fluid Mech. 468, 205–237.Google Scholar
Cisneros, L. H., Kessler, J. O., Ganguly, S. & Goldstein, R. E. 2011 Dynamics of swimming bacteria: transition to directional order at high concentration. Phys. Rev. E 83 (6), 061907.Google Scholar
Darwin, C. 1953 Note on hydrodynamics. Proc. Camb. Phil. Soc. 49, 342–354.Google Scholar
Dombrowski, C., Cisneros, L., Chatkaew, S., Goldstein, R. E. & Kessler, J. O. 2004 Self-concentration and large-scale coherence in bacterial dynamics. Phys. Rev. Lett. 93 (9), 098103.Google Scholar
Drescher, K., Dunkel, J., Cisneros, L. H., Ganguly, S. & Goldstein, R. E. 2011 Fluid dynamics and noise in bacterial cell–cell and cell–surface scattering. Proc. Natl Acad. Sci. USA 108 (27), 10940–10945.Google Scholar
Dunkel, J., Heidenreich, S., Drescher, K., Wensink, H. H., Bär, M. & Goldstein, R. E. 2013 Fluid dynamics of bacterial turbulence. Phys. Rev. Lett. 110 (22), 228102.Google Scholar
Evans, A. A., Ishikawa, T., Yamaguchi, T. & Lauga, E. 2011 Orientational order in concentrated suspensions of spherical microswimmers. Phys. Fluids 23 (11), 111702.Google Scholar
Ewald, P. P. 1921 Die berechnung optischer und elektrostatischer gitterpotentiale. Ann. Phys. 369 (3), 253–287.Google Scholar
Gachelin, J., Miño, G., Berthet, H., Lindner, A., Rousselet, A. & Clément, E. 2013 Non-newtonian viscosity of Escherichia coli suspensions. Phys. Rev. Lett. 110 (26), 268103.Google Scholar
Ghose, S. & Adhikari, R. 2014 Enhanced diffusion of nonswimmers in a three-dimensional bath of motile bacteria. Phys. Rev. Lett. 112 (11), 118102.Google Scholar
Grassia, P. S., Hinch, E. J. & Nitsche, L. C. 1995 Computer simulations of brownian motion of complex systems. J. Fluid Mech. 282, 373–403.Google Scholar
Gray, J. 1958 The movement of the spermatozoa of the bull. J. Expl Biol. 35 (1), 96–108.Google Scholar
Gray, J. & Hancock, G. J. 1955 The propulsion of sea-urchin spermatozoa. J. Expl Biol. 32 (4), 802–814.Google Scholar
Guasto, J. S., Johnson, K. A. & Gollub, J. P. 2010 Oscillatory flows induced by microorganisms swimming in two dimensions. Phys. Rev. Lett. 105 (16), 168102.Google Scholar
Hasimoto, H. 1959 On the periodic fundamental solutions of the stokes equations and their application to viscous flow past a cubic array of spheres. J. Fluid Mech. 5 (02), 317–328.Google Scholar
Hatwalne, Y., Ramaswamy, S., Rao, M. & Simha, A. R. 2004 Rheology of active-particle suspensions. Phys. Rev. Lett. 92, 118101.Google Scholar
Hernandez-Ortiz, J. P., Stoltz, C. G. & Graham, M. D. 2005 Transport and collective dynamics in suspensions of confined swimming particles. Phys. Rev. Lett. 95 (20), 204501.Google Scholar
Hernandez-Ortiz, J. P., Underhill, P. T. & Graham, M. D. 2009 Dynamics of confined suspensions of swimming particles. J. Phys.: Condens. Matter 21 (20), 204107.Google Scholar
Hill, N. A. & Pedley, T. J. 2005 Bioconvection. Fluid Dyn. Res. 37 (1), 1–20.Google Scholar
Hohenegger, C. & Shelley, M. J. 2010 Stability of active suspensions. Phys. Rev. E 81, 046311.Google Scholar
Ishikawa, T., Locsei, J. T. & Pedley, T. J. 2008 Development of coherent structures in concentrated suspensions of swimming model micro-organisms. J. Fluid Mech. 615, 401–431.Google Scholar
Ishikawa, T. & Pedley, T. J. 2007 The rheology of a semi-dilute suspension of swimming model micro-organisms. J. Fluid Mech. 588, 399–435.Google Scholar
Ishikawa, T. & Pedley, T. J. 2008 Coherent structures in monolayers of swimming particles. Phys. Rev. Lett. 100 (8), 088103.Google Scholar
Karmakar, R., Gulvady, R., Tirumkudulu, M. S. & Venkatesh, K. V. 2014 Motor characteristics determine the rheological behavior of a suspension of microswimmers. Phys. Fluids 26 (7), 071905.Google Scholar
Kasyap, T. V., Koch, D. L. & Wu, M. 2014 Hydrodynamic tracer diffusion in suspensions. Phys. Fluids 26, 081901.Google Scholar
Koch, D. L. & Subramanian, G. 2011 Collective hydrodynamics of swimming microorganisms: living fluids. Annu. Rev. Fluid Mech. 43, 637–659.Google Scholar
Krishnamurthy, D.2014 Heat transfer from drops in shearing flows and collective motion in micro-scale swimmer suspensions. Master’s thesis, Jawaharlal Nehru Centre for Advanced Scientific Research, Bangalore, India.Google Scholar
Larson, R. G. 1988 Constitutive Equations for Polymer Melts and Solutions. Butterworths.Google Scholar
Lauga, E. & Powers, T. R. 2009 The hydrodynamics of swimming microorganisms. Rep. Prog. Phys. 72 (9), 096601.Google Scholar
Leal, L. G. 2007 Advanced Transport Phenomena: Fluid Mechanics and Convective Transport Processes, vol. 7. Cambridge University Press.Google Scholar
Leptos, K. C., Guasto, J. S., Gollub, J. P., Pesci, A. I. & Goldstein, R. E. 2009 Dynamics of enhanced tracer diffusion in suspensions of swimming eukaryotic microorganisms. Phys. Rev. Lett. 103 (19), 198103.Google Scholar
Lin, Z., Thiffeault, J. L. & Childress, S. 2011 Stirring by squirmers. J. Fluid Mech. 669, 167–177.Google Scholar
Liu, B., Gulino, M., Morse, M., Tang, J. X., Powers, T. R. & Breuer, K. S. 2014 Helical motion of the cell body enhances Caulobacter crescentus motility. Proc. Natl Acad. Sci. USA 111 (31), 11252–11256.Google Scholar
Mackaplow, M. B. & Shaqfeh, E. S. G. 1998 A numerical study of the sedimentation of fibre suspensions. J. Fluid Mech. 376, 149–182.Google Scholar
Mehandia, V. & Nott, P. R. 2008 The collective dynamics of self-propelled particles. J. Fluid Mech. 595, 239–264.Google Scholar
Mendelson, N. H., Bourque, A., Wilkening, K., Anderson, K. R. & Watkins, J. C. 1999 Organized cell swimming motions in Bacillus subtilis colonies: patterns of short-lived whirls and jets. J. Bacteriol. 181 (2), 600–609.Google Scholar
Miño, G. L., Dunstan, J., Rousselet, A., Clément, E. & Soto, R. 2013 Induced diffusion of tracers in a bacterial suspension: theory and experiments. J. Fluid Mech. 729, 423–444.Google Scholar
Morozov, A. & Marenduzzo, D. 2014 Enhanced diffusion of tracer particles in dilute bacterial suspensions. Soft Matt. 10 (16), 2748–2758.Google Scholar
Narayan, V., Ramaswamy, S. & Menon, N. 2007 Long-lived giant number fluctuations in a swarming granular nematic. Science 317, 105–108.Google Scholar
Ordal, G. W. & Goldman, D. J. 1976 Chemotactic repellents of Bacillus subtilis . J. Molecular Biol. 100 (1), 103–108.Google Scholar
Polin, M., Tuval, I., Drescher, K., Gollub, J. P. & Goldstein, R. E. 2009 Chlamydomonas swims with two ‘gears’ in a eukaryotic version of run-and-tumble locomotion. Science 325 (5939), 487–490.Google Scholar
Purcell, E. M. 1977 Life at low Reynolds number. Am. J. Phys 45 (1), 3–11.Google Scholar
Pushkin, D. O., Shum, H. & Yeomans, J. M. 2013 Fluid transport by individual microswimmers. J. Fluid Mech. 726, 5–25.Google Scholar
Pushkin, D. O. & Yeomans, J. M. 2013 Fluid mixing by curved trajectories of microswimmers. Phys. Rev. Lett. 111 (18), 188101.Google Scholar
Pushkin, D. O. & Yeomans, J. M. 2014 Stirring by swimmers in confined microenvironments. J. Stat. Mech. 2014 (4), P04030.Google Scholar
Rahnama, M., Koch, D. L. & Shaqfeh, E. S. G. 1995 The effect of hydrodynamic interactions on the orientation distribution in a fiber suspension subject to simple shear flow. Phys. Fluids 7 (3), 487–506.Google Scholar
Rao, C. V., Kirby, J. R. & Arkin, A. P. 2004 Design and diversity in bacterial chemotaxis: a comparative study in Escherichia coli and Bacillus subtilis . PLoS Biol. 2 (2), 239–252.Google Scholar
Saintillan, D., Darve, E. & Shaqfeh, E. S. G. 2005 A smooth particle-mesh ewald algorithm for stokes suspension simulations: the sedimentation of fibers. Phys. Fluids 17 (3), 033301.Google Scholar
Saintillan, D. & Shelley, M. J. 2007 Orientational order and instabilities in suspensions of self-locomoting rods. Phys. Rev. Lett. 99 (5), 058102.Google Scholar
Saintillan, D. & Shelley, M. J. 2008a Instabilities and pattern formation in active particle suspensions: kinetic theory and continuum simulations. Phys. Rev. Lett. 100 (17), 178103.Google Scholar
Saintillan, D. & Shelley, M. J. 2008b Instabilities, pattern formation, and mixing in active suspensions. Phys. Fluids 20 (12), 123304.Google Scholar
Saintillan, D. & Shelley, M. J. 2012 Emergence of coherent structures and large-scale flows in motile suspensions. J. R. Soc. Interfaces 9 (68), 571–585.Google Scholar
Sandoval, M., Navaneeth, K. M., Subramanian, G. & Lauga, E. 2014 Stochastic dynamics of active swimmers in linear flows. J. Fluid Mech. 742, 50–70.Google Scholar
Sierou, A. & Brady, J. F. 2001 Accelerated stokesian dynamics simulations. J. Fluid Mech. 448, 115–146.Google Scholar
Simha, A. R. & Ramaswamy, S. 2002 Hydrodynamic fluctuations and instabilities in ordered suspensions of self-propelled particles. Phys. Rev. Lett. 89 (5), 058101,1–4.Google Scholar
Sokolov, A. & Aranson, I. S. 2009 Reduction of viscosity in suspension of swimming bacteria. Phys. Rev. Lett. 103 (14), 148101.Google Scholar
Sokolov, A. & Aranson, I. S. 2012 Physical properties of collective motion in suspensions of bacteria. Phys. Rev. Lett. 109, 248109.Google Scholar
Sokolov, A., Aranson, I. S., Kessler, J. O. & Goldstein, R. E. 2007 Concentration dependence of the collective dynamics of swimming bacteria. Phys. Rev. Lett. 98 (15), 158102.Google Scholar
Sokolov, A., Goldstein, R. E., Feldchtein, F. I. & Aranson, I. S. 2009 Enhanced mixing and spatial instability in concentrated bacterial suspensions. Phys. Rev. E 80 (3), 031903.Google Scholar
Soni, G. V., Ali, B. M. J., Hatwalne, Y. & Shivashankar, G. V. 2003 Single particle tracking of correlated bacterial dynamics. Biophys. J. 84 (4), 2634–2637.Google Scholar
Stocker, R. 2011 Reverse and flick: hybrid locomotion in bacteria. Proc. Natl Acad. Sci. USA 108 (7), 2635–2636.Google Scholar
Subramanian, G. & Koch, D. L. 2009 Critical bacterial concentration for the onset of collective swimming. J. Fluid Mech. 632, 359–400.Google Scholar
Subramanian, G., Koch, D. L. & Fitzgibbon, S. R. 2011 The stability of a homogeneous suspension of chemotactic bacteria. Phys. Fluids 23 (4), 041901.Google Scholar
Subramanian, G. & Nott, P. R. 2012 The fluid dynamics of swimming microorganisms and cells. J. IISc 91 (3), 283–314.Google Scholar
Thiffeault, J. L. & Childress, S. 2010 Stirring by swimming bodies. Phys. Lett. A 374 (34), 3487–3490.Google Scholar
Tuval, I., Cisneros, L., Dombrowski, C., Wolgemuth, C. W., Kessler, J. O. & Goldstein, R. E. 2005 Bacterial swimming and oxygen transport near contact lines. Proc. Natl Acad. Sci. USA 102 (7), 2277–2282.Google Scholar
Underhill, P. T., Hernandez-Ortiz, J. P. & Graham, M. D. 2008 Diffusion and spatial correlations in suspensions of swimming particles. Phys. Rev. Lett. 100 (24), 248101.Google Scholar
Wheatley, P. O. & Gerald, C. F. 1984 Applied Numerical Analysis. Addison-Wesley.Google Scholar
Wu, X. L. & Libchaber, A. 2000 Particle diffusion in a quasi-two-dimensional bacterial bath. Phys. Rev. Lett. 84 (13), 3017–3020.Google Scholar
Wu, M., Roberts, J. W., Kim, S., Koch, D. L. & DeLisa, M. P. 2006 Collective bacterial dynamics revealed using a three-dimensional population-scale deed particle tracking technique. Appl. Environ. Microbiol. 72 (7), 4987–4994.Google Scholar