Hostname: page-component-7bb8b95d7b-495rp Total loading time: 0 Render date: 2024-09-26T18:24:15.442Z Has data issue: false hasContentIssue false
  • English
  • Français

Collective diffusion in sheared colloidal suspensions

Published online by Cambridge University Press:  01 February 2008

ALEXANDER M. LESHANSKY ,
JEFFREY F. MORRIS  and
JOHN F. BRADY
ALEXANDER M. LESHANSKY
Affiliation:
Department of Chemical Engineering, Technion–IIT, Haifa, 32000, Israel
JEFFREY F. MORRIS
Affiliation:
Benjamin Levich Institute and Department of Chemical Engineering, City College of New York, New York, NY 10031, USA
JOHN F. BRADY
Affiliation:
Division of Chemistry & Chemical Engineering, California Institute of Technology, Pasadena, CA 91125, USA
Get access Rights & Permissions [Opens in a new window]

Abstract

Collective diffusivity in a suspension of rigid particles in steady linear viscous flows is evaluated by investigating the dynamics of the time correlation of long-wavelength density fluctuations. In the absence of hydrodynamic interactions between suspended particles in a dilute suspension of identical hard spheres, closed-form asymptotic expressions for the collective diffusivity are derived in the limits of low and high Péclet numbers, where the Péclet number 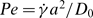with 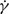being the shear rate and D0 = kBT/6πη a is the Stokes–Einstein diffusion coefficient of an isolated sphere of radius a in a fluid of viscosity η. The effect of hydrodynamic interactions is studied in the analytically tractable case of weakly sheared (Pe ≪ 1) suspensions.

For strongly sheared suspensions, i.e. at high Pe, in the absence of hydrodynamics the collective diffusivity Dc = 6 Ds∞, where Ds∞ is the long-time self-diffusivity and both scale as 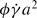, where φ is the particle volume fraction. For weakly sheared suspensions it is shown that the leading dependence of collective diffusivity on the imposed flow is proportional to D0 φPeÊ, where Ê is the rate-of-strain tensor scaled by 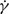, regardless of whether particles interact hydrodynamically. When hydrodynamic interactions are considered, however, correlations of hydrodynamic velocity fluctuations yield a weakly singular logarithmic dependence of the cross-gradient-diffusivity on k at leading order as ak → 0 with k being the wavenumber of the density fluctuation. The diagonal components of the collective diffusivity tensor, both with and without hydrodynamic interactions, are of O(φPe2), quadratic in the imposed flow, and finite at k = 0.

At moderate particle volume fractions, 0.10 ≤ φ ≤ 0.35, Brownian Dynamics (BD) numerical simulations in which there are no hydrodynamic interactions are performed and the transverse collective diffusivity in simple shear flow is determined via time evolution of the dynamic structure factor. The BD simulation results compare well with the derived asymptotic estimates. A comparison of the high-Pe BD simulation results with available experimental data on collective diffusivity in non-Brownian sheared suspensions shows a good qualitative agreement, though hydrodynamic interactions prove to be important at moderate concentrations.

Type
Papers
Information
Journal of Fluid Mechanics , Volume 597 , 25 February 2008 , pp. 305 - 341
Copyright
Copyright © Cambridge University Press 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Acrivos, A., Batchelor, G. K., Hinch, E. J., Koch, D. L. & Mauri, R. 1992 The longitudinal shear-induced diffusion of spheres in a dilute suspension. J. Fluid Mech. 240, 651–657.CrossRefGoogle Scholar
Batchelor, G. K. 1972 Sedimentation in a dilute dispersion of spheres. J. Fluid Mech. 52, 245–268.CrossRefGoogle Scholar
Batchelor, G. K. 1976 Brownian diffusion of particles with hydrodynamic interaction. J. Fluid Mech. 74, 1–29.CrossRefGoogle Scholar
Batchelor, G. K. 1977 The effect of Brownian motion on the bulk stress in a suspension of spherical particles. J. Fluid Mech. 83, 97–117.CrossRefGoogle Scholar
Batchelor, G. K. 1979 Mass transfer from a particle suspended in fluid with a steady linear ambient velocity distribution. J. Fluid Mech. 95, 369–400.CrossRefGoogle Scholar
Batchelor, G. K. & Green, J. T. 1972 The hydrodynamic interactions of two small freely-moving spheres in a linear flow field. J. Fluid Mech. 56, 375–400.CrossRefGoogle Scholar
Bergenholtz, J., Brady, J. F. & Vicic, M. A. 2002 The non-Newtonian rheology of dilute colloidal suspensions. J. Fluid Mech. 456, 239–275.CrossRefGoogle Scholar
Berne, B. J. & Pecora, R. 1976 Dynamic Light Scattering. Wiley.Google Scholar
Bławzdziewicz, J. & Szamel, G. 1993 Structure and rheology of semidilute suspensions under shear Phys. Rev. E. 48, 4632–4636.Google ScholarPubMed
Brady, J. F. 1994 The long-time self-diffusivity in concentrated colloidal dispersions. J. Fluid Mech. 272, 109–134.CrossRefGoogle Scholar
Brady, J. F. & Morris, J. F. 1997 Microstructure of strongly sheared suspensions and its impact on rheology and diffusion. J. Fluid Mech 348, 103–139.CrossRefGoogle Scholar
Brady, J. F., Phillips, R. J., Lester, J. C. & Bossis, G. 1988 Dynamic simulation of hydrodynamically interacting suspensions. J. Fluid Mech. 195, 257–280.CrossRefGoogle Scholar
Brady, J. F. & Vicic, M. 1995 Normal stresses in colloidal dispersions. J. Rheol. 40, 545–566.CrossRefGoogle Scholar
Breedveld, V., vanden Ende, D. den Ende, D., Triphati, A. & Acrivos, A. 1998 The measurement of the shear-induced particle and fluid tracer diffusivities by a novel method. J. Fluid Mech. 375, 297–318.CrossRefGoogle Scholar
Caflisch, R. E. & Luke, J. H. C. 1985 Variance in the sedimentation speed of a suspension. Phys. Fluids 28, 759–760.CrossRefGoogle Scholar
daCunha, F. R. Cunha, F. R. & Hinch, E. J. 1996 Shear-induced disperion in a dilute suspension of rough spheres. J. Fluid Mech. 309, 211–223.Google Scholar
Dhont, J. K. G. 1996 An Introduction to the Dynamics of Colloids. Elsevier.Google Scholar
Drazer, G., Koplik, J., Khusid, B. & Acrivos, A. 2002 Deterministic and stochastic behaviour of non-Brownian spheres in sheared suspensions. J. Fluid Mech. 460, 307–335.CrossRefGoogle Scholar
Eckstein, E. C., Bailey, D. C. & Shapiro, A. H. 1977 Self-diffusion of particles in shear-flow of a suspension. J. Fluid Mech. 79, 191–208.CrossRefGoogle Scholar
Einstein, A. 1905 On the movement of small particles suspended in stationary liquids required by the molecular-kinetic theory of heat. Annalen der Phys. 17, 549–560.CrossRefGoogle Scholar
Elrick, D. E. 1962 Source functions for diffusion in uniform shear flow. Austral. J. Phys. 15, 283–288.CrossRefGoogle Scholar
Foss, D. R. & Brady, J. F. 1999 Self-diffusion in sheared suspensions by dynamic simulation. J. Fluid Mech. 401, 243–274.CrossRefGoogle Scholar
Frankel, I. & Brenner, H. 1991 Generalized Taylor dispersion phenomena in unbounded homogeneous shear flows. J. Fluid Mech. 230, 147–181.CrossRefGoogle Scholar
Heyes, D. M. & Melrose, J. R. 1993 Brownian dynamics simulations of model hard-sphere suspensions. J. Non-Newtonian Fluid Mech. 46, 1–28.CrossRefGoogle Scholar
Hinch, E. J. 1977 An averaged-equation approach to particle interactions in a fluid suspension. J. Fluid Mech. 83, 695–720.CrossRefGoogle Scholar
Jeffrey, D. J. & Onishi, Y. 1984 Calculation of the resistance and mobility functions for two unequal rigid spheres in low-Reynolds-number flow. J. Fluid Mech. 139, 261–290.CrossRefGoogle Scholar
Johnson, S. J., deKruif, C. G. Kruif, C. G. & May, R. P. 1988 Structure factor distortion for hard-sphere dispersions subjected to weak shear flow: Small-angle neutron scattering in the flow-vorticity plane. J. Chem. Phys. 89, 5909–5921.CrossRefGoogle Scholar
Kim, S. & Karrila, S. J. 1991 Microhydrodynamics: Principles and Selected Applications. Butterworth-Heinemann.Google Scholar
de Kruif, C. G., van der Werff, J. C., Johnson, S. J. & May, R. P. 1990 Small-angle neutron scattering of sheared concentrated dispersions: Microstructure along principal axes. Phys. Fluids A 2, 1545–1556.CrossRefGoogle Scholar
Leighton, D. T. & Acrivos, A. 1987 The shear-induced migration of particles in concentrated suspensions. J. Fluid Mech. 181, 415–439.CrossRefGoogle Scholar
Leshansky, A. M. & Brady, J. F. 2005 Dynamic structure factor study of diffusion in strongly sheared suspensions. J. Fluid Mech. 527, 141–169.CrossRefGoogle Scholar
Marchioro, M. & Acrivos, A. 2001 Shear-induced particle diffusivities from numerical simuations. J. Fluid Mech. 443, 101–128.CrossRefGoogle Scholar
Mauri, R. 2003 The constitutive relation of suspensions of non-colloidal particles in viscous fluids. Phys. Fluids 15, 1888–1896.CrossRefGoogle Scholar
sanMiguel, M. Miguel, M. & Sancho, J. M. 1979 Brownian motion in shear flow. Physica A 99, 357–364.Google Scholar
Morris, J. F. & Brady, J. F. 1996 Self-diffusion in sheared suspensions. J. Fluid Mech. 312, 223–252.CrossRefGoogle Scholar
Morris, J. F. & Katyal, B. 2002 Microstructure from simulated Brownian suspension flows at large shear rate. Phys. Fluids 14, 1920–1937.CrossRefGoogle Scholar
Novikov, E. A. 1958 Concerning turbulent diffusion in a stream with transverse gradient of velocity. Prikl. Mat. Mech. 22, 412–414 (in Russian).Google Scholar
Pusey, P. N. 1991 Colloidal suspensions. In Liquids, Freezing and Glass Transitions (ed. Hansen, J. P., Levesque, D. & Zinn-Justin, J.). Elsevier.Google Scholar
Rallison, J. M. & Hinch, E. J. 1986 The effect of particle interactions on dynamic light scattering from a dilute suspension. J. Fluid Mech. 167, 131–168.CrossRefGoogle Scholar
Russel, W. B. & Glendinning, A. B. 1981 The effective diffusion coefficient detected by dynamic light scattering. J. Chem. Phys. 72, 948–952.CrossRefGoogle Scholar
Russel, W. B., Saville, D. A. & Schowalter, W. R. 1989 Colloidal Dispersions. Cambridge University Press.CrossRefGoogle Scholar
Schaertl, W. & Sillescu, H. 1994 Brownian dynamics simulations of colloidal hard spheres. Effects of sample dimensionality on self-diffusion. J. Statist. Phys. 74, 687–703.CrossRefGoogle Scholar
Segré, P. N., Behrend, O. P. & Pusey, P. N. 1995 Short-time Brownian motion in colloidal suspenions: Experiment and simulation. Phys. Rev. E 52, 5070–5083.Google ScholarPubMed
Sierou, A. & Brady, J. F. 2001 Accelerated Stokesian Dynamics simulations. J. Fluid Mech. 448, 115–146.CrossRefGoogle Scholar
Sierou, A. & Brady, J. F. 2004 Shear-induced self-diffusion in non-colloidal suspensions. J. Fluid Mech. 506, 285–314.CrossRefGoogle Scholar
Taylor, G. I. 1953 Dispersion of soluble matter in solvent flowing slowly through a tube. Proc. Roy. Soc. Lond. A 219, 186–203.Google Scholar
Vermant, J. & Solomon, M. J. 2005 Flow induced structure in colloidal suspensions. J. Phys.-Cond. Matter 17, R187–R216.CrossRefGoogle Scholar
Vicic, M. 1999 Rheology and microstructure of complex fluids: Dispersions, emulsions and polymer solutions. PhD dissertation, California Institute of Technology.Google Scholar
Wagner, N. J. & Russel, W. B. 1990 Light scattering experiments of a hard-sphere suspension under shear. Phys. Fluids A 2, 491–502.CrossRefGoogle Scholar
Wang, Y. & Mauri, R. 1999 Longitudinal shear-induced gradient diffusion in a dilute suspension of spheres. Intl J. Multiphase Flow 25, 875–885.CrossRefGoogle Scholar
Wang, Y., Mauri, R. & Acrivos, A. 1996 The transverse shear-induced liquid and particle tracer diffusivities of a dilute suspension of spheres undergoing a simple shear flow. J. Fluid Mech. 327, 255–272.CrossRefGoogle Scholar
Wang, Y., Mauri, R. & Acrivos, A. 1998 Transverse shear-induced gradient diffusion of a dilute suspension of spheres. J. Fluid Mech. 357, 279–287.CrossRefGoogle Scholar