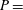1 Introduction
Turbulent buoyant plumes transporting relatively dense particles can be found in natural and engineered environments, including volcanoes, black smokers rising from deep-sea vents, dredging operations, effluent from marine outfalls and particles from combustion in fires or engines. Where plumes rise from a source of buoyancy through a stratified ambient fluid (common in oceanic and atmospheric environments) the rising plume entrains ambient fluid and eventually reaches a point where the plume density is equal to the local ambient density and the plume fluid spreads horizontally as a radial intrusion (Morton, Taylor & Turner Reference Morton, Taylor and Turner1956; Carrazzo & Jellinek Reference Carrazzo and Jellinek2012; Richards, Aubourg & Sutherland Reference Richards, Aubourg and Sutherland2014; Mirajkar & Balasubramanian Reference Mirajkar and Balasubramanian2017). If the plume contains dense particles then these will drop out from the intrusion and begin to fall through the ambient fluid (Sparks, Carey & Sigurdsson Reference Sparks, Carey and Sigurdsson1991). If the particles fall close enough to the rising plume, they may be re-entrained, increasing the flux of particles within the plume and reducing its buoyancy (Carey, Sigurdsson & Sparks Reference Carey, Sigurdsson and Sparks1988; Veitch & Woods Reference Veitch and Woods2000; Zarrebini & Cardoso Reference Zarrebini and Cardoso2000) – see figure 1.
Most theoretical work on this problem has considered extremely small particle concentrations, where the dense particles have a negligible effect on the overall buoyancy of the plume. Many laboratory studies have used water as a working fluid, where the relative density of solid particles is not very large. However, in air, even small volume concentrations of particles can make substantial differences to the buoyancy of a plume. This is because the difference between particle and fluid densities may be several orders of magnitude higher than the relative density difference between plume and ambient fluid, which is often only a few per cent. If the particle concentration is sufficiently high, the resulting negative buoyancy contribution may overcome the initial plume buoyancy, causing the plume to collapse once sufficient particles have been re-entrained.
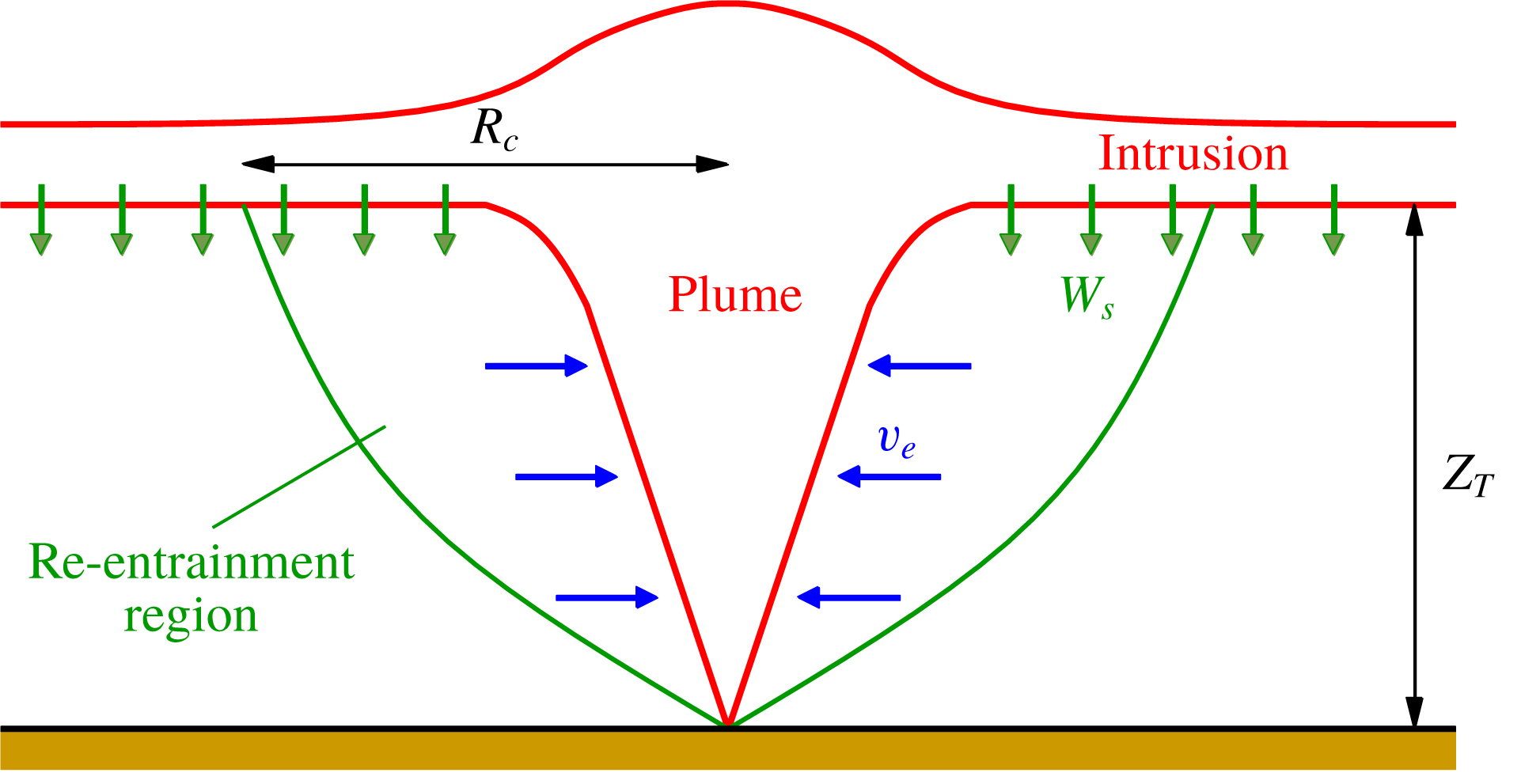
Figure 1. Schematic of particle-laden buoyant plume in a stratified ambient fluid.
Many previous laboratory studies have considered plume rise and particle fallout in an unstratified, depth-limited surrounding medium, where the horizontal layer is a gravity current spreading radially along the free surface (Carey et al. Reference Carey, Sigurdsson and Sparks1988; Sparks et al. Reference Sparks, Carey and Sigurdsson1991; Ernst et al. Reference Ernst, Sparks, Carey and Bursik1996; Veitch & Woods Reference Veitch and Woods2000; Zarrebini & Cardoso Reference Zarrebini and Cardoso2000). Others have considered the injection of a negatively buoyant ‘turbulent fountain’ (Carrazzo & Jellinek Reference Carrazzo and Jellinek2012), where the particle load is such that the overall density exceeds its surroundings, but is initially propelled upward by source momentum. However, our paper will focus on initially buoyant, homogeneous or particle-laden plumes whose height of rise is limited by ambient density stratification. This is more challenging to produce in the laboratory, but experimental work on particle-laden plume development in a stratified medium has been performed by Mirajkar, Tirodkar & Balasubramanian (Reference Mirajkar, Tirodkar and Balasubramanian2015) and Sutherland & Hong (Reference Sutherland and Hong2016).
Carey et al. (Reference Carey, Sigurdsson and Sparks1988) injected particle-laden fresh water into uniform salty water. They described the ‘veil of sedimenting particles’ around the plume margins, concluding that re-entrained particles had a significant effect on the plume dynamics through their influence on plume buoyancy. They identified four types of plume collapse behaviour: dilute downward-moving gravity flows along plume margins; instability leading to an asymmetrical bent-over collapse; low-collapsing fountain; and collapse of umbrella region. Using a similar experimental configuration, Sparks et al. (Reference Sparks, Carey and Sigurdsson1991) investigated the concentration distribution in the free-surface gravity current and subsequent deposition pattern formed by fallout when a particle-laden fresh-water plume reached the surface of a uniformly saline tank. They determined that, for lighter sediment carried all the way to the free surface, the concentration in the gravity current and subsequent deposition distribution on the floor was consistent with an exponentially decaying radial concentration distribution and a critical radius within which sedimenting particles are drawn back into the rising plume. They also noted that this simple theory did not apply for heavier particles, for which the critical radius was less than the plume-to-gravity-current ‘corner’, where particles fell out from the plume margins during its rise phase. Ernst et al. (Reference Ernst, Sparks, Carey and Bursik1996) examined the re-entrainment of these heavier particles for both momentum-dominated jets and buoyancy-dominated plumes, modelling fallout rate as a function of the settling velocity and local spreading rate of the plume and re-entrainment using an empirical ‘re-entrainment’ coefficient. Their modelling and subsequent comparison with measured data emphasised the important role of re-entrainment in amplifying near-field deposition. Veitch & Woods (Reference Veitch and Woods2000) continued the ‘fallout-from-umbrella-cloud’ model of Sparks et al. (Reference Sparks, Carey and Sigurdsson1991), but this time considered the role of the non-depositing fraction that was re-entrained into the plume, reducing its overall buoyancy and contributing to an oscillatory collapse mechanism. Cardoso & Zarrebini (Reference Cardoso and Zarrebini2001a ) observed that, for particles falling out of a surface layer into uniform-density fluid, the resulting unstable density distribution in the ambient fluid can under some circumstances – low settling velocity and high source concentration – drive convection. This is much less likely to occur in our scenario, as the background fluid is stably density stratified and the horizontal intrusion, forming at its natural neutral layer, is more dilute than one obliged to spread at a free surface.
Whilst most laboratory studies have used a single particle size, Cardoso & Zarrebini (Reference Cardoso and Zarrebini2001b ) used polydisperse particulate. Their model, validated by laboratory measurements of deposition fluxes, integrated paths of settling particles in a velocity field determined by plume entrainment, and determined the radial distribution of deposition.
For circumstances where plume rise is limited by the ambient density profile (e.g. in the atmosphere), rather than a free-surface rigid lid (as in most laboratory tank-based studies), there is initial overshoot of the final intrusion height, because the plume reaches the neutral-density level with non-zero momentum. This region plays a role in determining the final height of the intrusion because the plume continues to entrain particulate-free fluid. The quantity and density of fluid entrained here dictates the level at which final plume density will match that of the surrounds and form an intrusion. Once the intrusion has formed, however, the sedimentation behaviour below it is similar to that for a free-surface gravity current.
In a stationary stratified medium, plume- or jet-like behaviour of injected material is associated with the parameter
![]() $(M_{0}/B_{0})N$
, where
$(M_{0}/B_{0})N$
, where
![]() $M_{0}$
and
$M_{0}$
and
![]() $B_{0}$
are initial momentum and buoyancy flux, respectively, and
$B_{0}$
are initial momentum and buoyancy flux, respectively, and
![]() $N$
is the buoyancy frequency. (These quantities will be formally defined in § 2.) Typically, values less than 0.1 are classified as plumes, and values greater than 2 are classified as jets; injections with intermediate values are variously described as ‘buoyant jet’ or ‘forced plume’. We examine experimental data for the maximum rise height,
$N$
is the buoyancy frequency. (These quantities will be formally defined in § 2.) Typically, values less than 0.1 are classified as plumes, and values greater than 2 are classified as jets; injections with intermediate values are variously described as ‘buoyant jet’ or ‘forced plume’. We examine experimental data for the maximum rise height,
![]() $Z_{max}$
, and final intrusion height,
$Z_{max}$
, and final intrusion height,
![]() $Z_{T}$
.
$Z_{T}$
.
Mirajkar et al. (Reference Mirajkar, Tirodkar and Balasubramanian2015) and Sutherland & Hong (Reference Sutherland and Hong2016) both considered the injection of water with varying particle content into linearly stratified tanks. Mirajkar et al. conducted all their experiments at a single value,
![]() $(M_{0}/B_{0})N=0.87$
, whilst Sutherland and Hong used values between 1.31 and 2.17; thus, these emissions correspond to forced plumes. Mirajkar et al. fitted their data with an empirical expression for the maximum rise:
$(M_{0}/B_{0})N=0.87$
, whilst Sutherland and Hong used values between 1.31 and 2.17; thus, these emissions correspond to forced plumes. Mirajkar et al. fitted their data with an empirical expression for the maximum rise:
where
![]() $W_{s}$
is settling velocity, indicating the reduction in maximum height with particle concentration. The maximum height for particle-free plumes,
$W_{s}$
is settling velocity, indicating the reduction in maximum height with particle concentration. The maximum height for particle-free plumes,
![]() $4.4(B_{0}/N^{3})^{1/4}$
, is larger than that cited by Morton et al. (Reference Morton, Taylor and Turner1956), where the constant is 3.79. The difference arises from the fact that Mirajkar et al.’s experiments used buoyant jets rather than pure plumes. Sutherland & Hong (Reference Sutherland and Hong2016) proposed an empirical fit to their data for the intrusion height of the form
$4.4(B_{0}/N^{3})^{1/4}$
, is larger than that cited by Morton et al. (Reference Morton, Taylor and Turner1956), where the constant is 3.79. The difference arises from the fact that Mirajkar et al.’s experiments used buoyant jets rather than pure plumes. Sutherland & Hong (Reference Sutherland and Hong2016) proposed an empirical fit to their data for the intrusion height of the form
where
![]() $H_{P}=(M_{0}^{3}/B_{0}^{2})^{1/4}$
is a characteristic height above the source at which buoyancy effects begin to dominate over momentum. They also measured particle deposition from the intrusion layer as a function of radius, noting the effect of sedimenting particles being drawn back toward the plume by entrainment, and developed a particle trajectory model for recycling.
$H_{P}=(M_{0}^{3}/B_{0}^{2})^{1/4}$
is a characteristic height above the source at which buoyancy effects begin to dominate over momentum. They also measured particle deposition from the intrusion layer as a function of radius, noting the effect of sedimenting particles being drawn back toward the plume by entrainment, and developed a particle trajectory model for recycling.
Carrazzo & Jellinek (Reference Carrazzo and Jellinek2012) injected particle-laden jets into a two-layer salinity-stratified tank. Higher-velocity jets penetrated the interface between salt and fresh water (to an initial height dependent on their momentum and the ambient density step) and then fell back to spread as an ‘umbrella cloud’ along the interface. Different particle loading and source Froude numbers provoked various sedimentation regimes, from stable plume (but with particle cloud instabilities in the umbrella cloud) to total collapse. In contrast to the other experiments noted above, Carrazzo and Jellinek used negatively buoyant sources; for large particles this led to complete collapse of the turbulent fountain, subsequently spreading as a bed gravity current. This is a rather different mechanism from that envisaged in the present paper.
In this paper we model the development of particle concentration in a plume over time, following it to the point of either steady intrusion height or plume collapse. There are two levels of modelling: an integral plume model with discrete particle-recycling events in § 2, and a more advanced numerical model in § 3. In § 2 we first recap integral models for homogeneous plumes. Past formulations have used various different forms for some terms (e.g. including or not a factor of
![]() $\unicode[STIX]{x03C0}$
in some fluxes, including or not the entrainment coefficient in the non-dimensional scaling, and using top-hat or Gaussian-plume profiles). This leads to some confusion, so here we restate all the key equations and results in a coherent form. We also identify an invariant in the case of linear stratification that appears not to have been noticed hitherto in the literature. We then develop a model of particle re-entrainment, which gives initial estimates of conditions and time scales for plume collapse, and an estimate of the effect of particle loading on final height for non-collapsing plumes. In § 3 we develop, and show results for, a more detailed numerical model, with simplified CFD (computational fluid dynamics) used to solve a concentration equation in the region outside the plume. This allows us to calculate both the time development of the particle distribution and the effect of re-entraining particles on plume buoyancy and intrusion height (including time to collapse), as well as particles falling out during the rise phase. Finally, in § 4, we discuss our results and the implications for practical applications.
$\unicode[STIX]{x03C0}$
in some fluxes, including or not the entrainment coefficient in the non-dimensional scaling, and using top-hat or Gaussian-plume profiles). This leads to some confusion, so here we restate all the key equations and results in a coherent form. We also identify an invariant in the case of linear stratification that appears not to have been noticed hitherto in the literature. We then develop a model of particle re-entrainment, which gives initial estimates of conditions and time scales for plume collapse, and an estimate of the effect of particle loading on final height for non-collapsing plumes. In § 3 we develop, and show results for, a more detailed numerical model, with simplified CFD (computational fluid dynamics) used to solve a concentration equation in the region outside the plume. This allows us to calculate both the time development of the particle distribution and the effect of re-entraining particles on plume buoyancy and intrusion height (including time to collapse), as well as particles falling out during the rise phase. Finally, in § 4, we discuss our results and the implications for practical applications.
2 Simple plume model and estimates of collapse conditions
2.1 Non-particulate plume model
We assume an isolated plume emerges from a buoyant source, with initial total buoyancy
![]() $B_{0}$
rising in an unconfined, stationary, stratified ambient fluid of buoyancy frequency
$B_{0}$
rising in an unconfined, stationary, stratified ambient fluid of buoyancy frequency
![]() $N$
. For simplicity, we focus on the case where fluxes of mass and momentum at the source are zero, so that we have a ‘pure’ plume rising from a point source. In many practical cases with a source of finite size, the results will be very similar, provided that one integrates back to a ‘virtual origin’ and the vertical distances are offset appropriately. This type of flow has been studied by many authors since the seminal paper of Morton et al. (Reference Morton, Taylor and Turner1956), with the problem closed by assuming that the horizontal entrainment velocity of ambient fluid into the plume is proportional to the local vertical plume speed,
$N$
. For simplicity, we focus on the case where fluxes of mass and momentum at the source are zero, so that we have a ‘pure’ plume rising from a point source. In many practical cases with a source of finite size, the results will be very similar, provided that one integrates back to a ‘virtual origin’ and the vertical distances are offset appropriately. This type of flow has been studied by many authors since the seminal paper of Morton et al. (Reference Morton, Taylor and Turner1956), with the problem closed by assuming that the horizontal entrainment velocity of ambient fluid into the plume is proportional to the local vertical plume speed,
![]() $W$
, their ratio being called the ‘entrainment coefficient’,
$W$
, their ratio being called the ‘entrainment coefficient’,
![]() $\unicode[STIX]{x1D6FC}$
(Turner Reference Turner1986). Models typically assume either a ‘top-hat’ formulation, where fluid properties are assumed to jump from the ambient values outside the local plume radius,
$\unicode[STIX]{x1D6FC}$
(Turner Reference Turner1986). Models typically assume either a ‘top-hat’ formulation, where fluid properties are assumed to jump from the ambient values outside the local plume radius,
![]() $R$
, to constant local plume values inside, or Gaussian profiles, where velocity, density deficit and (in principle) particle concentration have an
$R$
, to constant local plume values inside, or Gaussian profiles, where velocity, density deficit and (in principle) particle concentration have an
![]() $\exp (-r^{2}/R^{2})$
dependence and
$\exp (-r^{2}/R^{2})$
dependence and
![]() $W$
and
$W$
and
![]() $g^{\prime }$
signify values on the plume centreline. In this section, in order to extract information from past literature, we allow for either scenario, but later sections will use exclusively top-hat profiles. Writing
$g^{\prime }$
signify values on the plume centreline. In this section, in order to extract information from past literature, we allow for either scenario, but later sections will use exclusively top-hat profiles. Writing
![]() $Q(=\unicode[STIX]{x03C0}R^{2}W)$
for the volume flux,
$Q(=\unicode[STIX]{x03C0}R^{2}W)$
for the volume flux,
![]() $M(=QW/\unicode[STIX]{x1D6FE})$
for the specific momentum flux and
$M(=QW/\unicode[STIX]{x1D6FE})$
for the specific momentum flux and
![]() $B(=Qg^{\prime }/\unicode[STIX]{x1D6FE})$
for the specific buoyancy flux, with
$B(=Qg^{\prime }/\unicode[STIX]{x1D6FE})$
for the specific buoyancy flux, with
![]() $\unicode[STIX]{x1D6FE}=1$
for top-hat and
$\unicode[STIX]{x1D6FE}=1$
for top-hat and
![]() $\unicode[STIX]{x1D6FE}=2$
for Gaussian plumes, we have the classic equations:
$\unicode[STIX]{x1D6FE}=2$
for Gaussian plumes, we have the classic equations:
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}{\displaystyle \frac{\text{d}Q}{\text{d}Z}}=E,\\ {\displaystyle \frac{\text{d}M}{\text{d}Z}}=g^{\prime }A,\\ {\displaystyle \frac{\text{d}B}{\text{d}Z}}=-N^{2}Q,\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}{\displaystyle \frac{\text{d}Q}{\text{d}Z}}=E,\\ {\displaystyle \frac{\text{d}M}{\text{d}Z}}=g^{\prime }A,\\ {\displaystyle \frac{\text{d}B}{\text{d}Z}}=-N^{2}Q,\end{array}\right\}\end{eqnarray}$$
where entrainment rate (
![]() $E$
), cross-sectional area (
$E$
), cross-sectional area (
![]() $A$
) and reduced gravity (
$A$
) and reduced gravity (
![]() $g^{\prime }$
) are given by
$g^{\prime }$
) are given by
Note that
![]() $g^{\prime }$
is the local reduced gravity, referenced to ambient density
$g^{\prime }$
is the local reduced gravity, referenced to ambient density
![]() $\unicode[STIX]{x1D70C}_{a}$
at that height, and not the global reference density
$\unicode[STIX]{x1D70C}_{a}$
at that height, and not the global reference density
![]() $\unicode[STIX]{x1D70C}_{0}$
. In this section we assume that
$\unicode[STIX]{x1D70C}_{0}$
. In this section we assume that
![]() $N$
is constant.
$N$
is constant.
Reflecting differences in the literature, we non-dimensionalise in two stages: with and without entrainment coefficient
![]() $\unicode[STIX]{x1D6FC}$
in the scaling. First we use dimensional scales
$\unicode[STIX]{x1D6FC}$
in the scaling. First we use dimensional scales
![]() $B_{0}$
and
$B_{0}$
and
![]() $N$
to give
$N$
to give
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}{\displaystyle \frac{\text{d}\tilde{Q}}{\text{d}\tilde{Z}}}=2\unicode[STIX]{x1D6FC}\sqrt{\unicode[STIX]{x1D6FE}\unicode[STIX]{x03C0}\tilde{M}},\\ {\displaystyle \frac{\text{d}\tilde{M}}{\text{d}\tilde{Z}}}={\displaystyle \frac{\tilde{B}\tilde{Q}}{\tilde{M}}},\\ {\displaystyle \frac{\text{d}\tilde{B}}{\text{d}\tilde{Z}}}=-\tilde{Q},\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}{\displaystyle \frac{\text{d}\tilde{Q}}{\text{d}\tilde{Z}}}=2\unicode[STIX]{x1D6FC}\sqrt{\unicode[STIX]{x1D6FE}\unicode[STIX]{x03C0}\tilde{M}},\\ {\displaystyle \frac{\text{d}\tilde{M}}{\text{d}\tilde{Z}}}={\displaystyle \frac{\tilde{B}\tilde{Q}}{\tilde{M}}},\\ {\displaystyle \frac{\text{d}\tilde{B}}{\text{d}\tilde{Z}}}=-\tilde{Q},\end{array}\right\}\end{eqnarray}$$
where
The non-dimensional entrainment constant
![]() $\unicode[STIX]{x1D6FC}$
appears in the first of (2.3) only. An
$\unicode[STIX]{x1D6FC}$
appears in the first of (2.3) only. An
![]() $\unicode[STIX]{x1D6FC}$
-independent problem may be derived by a second,
$\unicode[STIX]{x1D6FC}$
-independent problem may be derived by a second,
![]() $\unicode[STIX]{x1D6FC}$
-dependent, scaling as
$\unicode[STIX]{x1D6FC}$
-dependent, scaling as
to give:
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}{\displaystyle \frac{\text{d}q}{\text{d}z}}=2\sqrt{\unicode[STIX]{x1D6FE}\unicode[STIX]{x03C0}m},\\ {\displaystyle \frac{\text{d}m}{\text{d}z}}={\displaystyle \frac{bq}{m}},\\ {\displaystyle \frac{\text{d}b}{\text{d}z}}=-q.\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}{\displaystyle \frac{\text{d}q}{\text{d}z}}=2\sqrt{\unicode[STIX]{x1D6FE}\unicode[STIX]{x03C0}m},\\ {\displaystyle \frac{\text{d}m}{\text{d}z}}={\displaystyle \frac{bq}{m}},\\ {\displaystyle \frac{\text{d}b}{\text{d}z}}=-q.\end{array}\right\}\end{eqnarray}$$
Note, however, that for this second non-dimensionalisation the horizontal scale is
![]() $\unicode[STIX]{x1D6FC}$
times the vertical scale, since absolute radius
$\unicode[STIX]{x1D6FC}$
times the vertical scale, since absolute radius
![]() $R$
and height
$R$
and height
![]() $Z$
are given by
$Z$
are given by
Note also that entrainment coefficients reflect the choice of reference velocity for the plume profile. From (2.3),
Since the turbulent entrainment mechanism is different,
![]() $\unicode[STIX]{x1D6FC}$
also depends on the type of injection. Typical values of
$\unicode[STIX]{x1D6FC}$
also depends on the type of injection. Typical values of
![]() $\unicode[STIX]{x1D6FC}$
for a Gaussian plume are 0.054 (jets) and 0.083 (plumes) – see Turner (Reference Turner1986). The corresponding values for top-hat profiles are 0.076 and 0.12, respectively.
$\unicode[STIX]{x1D6FC}$
for a Gaussian plume are 0.054 (jets) and 0.083 (plumes) – see Turner (Reference Turner1986). The corresponding values for top-hat profiles are 0.076 and 0.12, respectively.
Figure 2 shows the result of integrating (2.8) (with top-hat profiles:
![]() $\unicode[STIX]{x1D6FE}=1$
) from an origin where the volume and momentum fluxes are zero. The plume has the same density as the ambient fluid at a height of
$\unicode[STIX]{x1D6FE}=1$
) from an origin where the volume and momentum fluxes are zero. The plume has the same density as the ambient fluid at a height of
![]() $1.038l_{s}$
, although the plume will overshoot this, as velocity does not become zero until
$1.038l_{s}$
, although the plume will overshoot this, as velocity does not become zero until
![]() $1.366l_{s}$
. Corresponding values for a Gaussian plume,
$1.366l_{s}$
. Corresponding values for a Gaussian plume,
![]() $\unicode[STIX]{x1D6FE}=2.0$
, are
$\unicode[STIX]{x1D6FE}=2.0$
, are
![]() $0.87l_{s}$
and
$0.87l_{s}$
and
![]() $1.15l_{s}$
, as in Morton et al. (Reference Morton, Taylor and Turner1956) – the different (by a factor of
$1.15l_{s}$
, as in Morton et al. (Reference Morton, Taylor and Turner1956) – the different (by a factor of
![]() $2^{1/4}$
) rise values in non-dimensional variables reflecting the different
$2^{1/4}$
) rise values in non-dimensional variables reflecting the different
![]() $\unicode[STIX]{x1D6FC}$
values for the different assumed plume profiles and reference velocities. The volume fluxes at the start and end of the overshoot region are
$\unicode[STIX]{x1D6FC}$
values for the different assumed plume profiles and reference velocities. The volume fluxes at the start and end of the overshoot region are
![]() $2.49q_{s}$
and
$2.49q_{s}$
and
![]() $3.52q_{s}$
(for top-hat plumes) whilst the momentum fluxes at corresponding positions are precisely
$3.52q_{s}$
(for top-hat plumes) whilst the momentum fluxes at corresponding positions are precisely
![]() $B_{0}/N$
and 0 and the buoyancy fluxes are 0 and
$B_{0}/N$
and 0 and the buoyancy fluxes are 0 and
![]() $-B_{0}$
for both types of plume profile (see § 2.2 below).
$-B_{0}$
for both types of plume profile (see § 2.2 below).
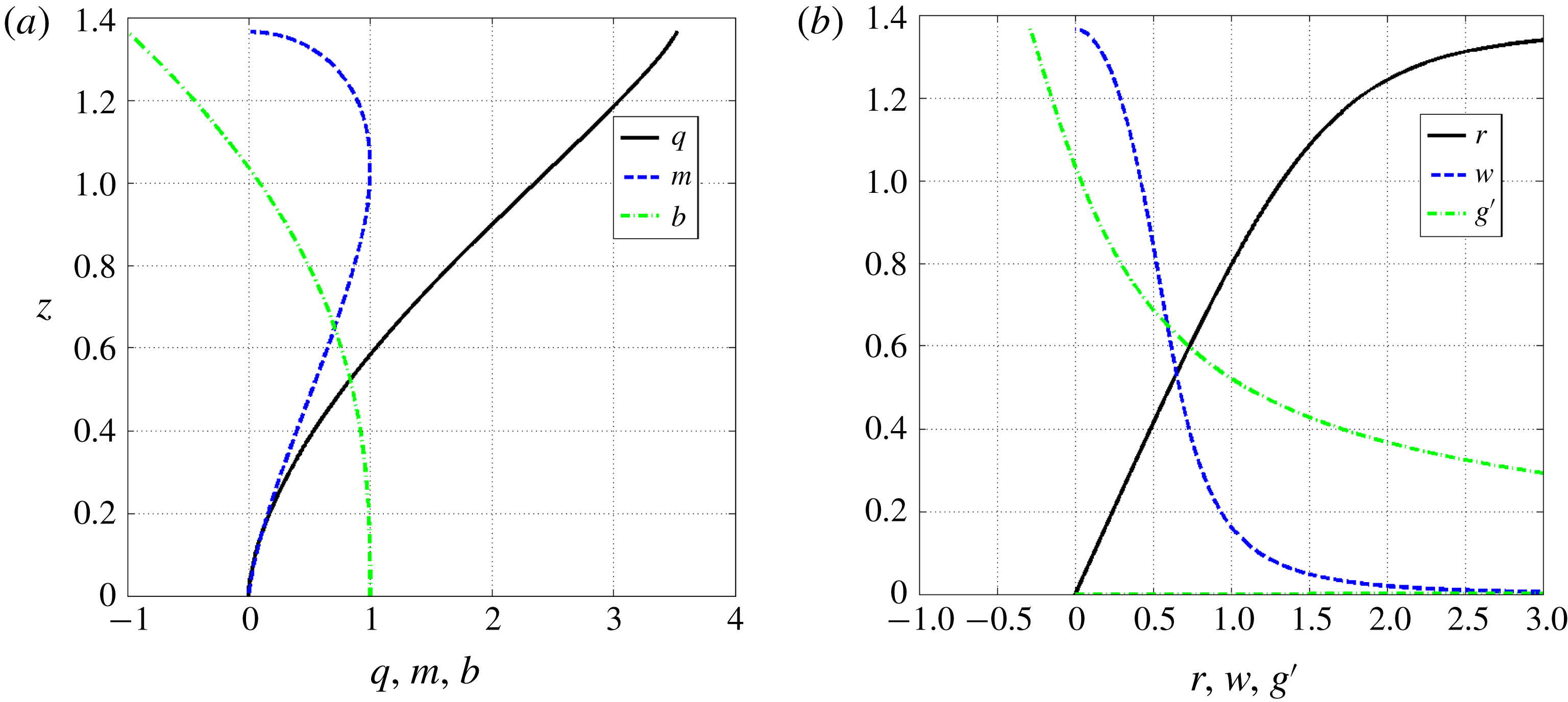
Figure 2. Top-hat integral model for a pure plume; (a) volume, momentum and buoyancy fluxes; (b) radius, velocity and reduced gravity. Variables scaled according to (2.6).
The plume model is not strictly applicable in the overshoot region, as the plume fluid falls back around the rising plume as a ‘curtain’, raising the density of fluid entrained into the rising column above that of ambient fluid. However, for pure plumes, the effect appears to be small. The laboratory experiments reported in Morton et al. (Reference Morton, Taylor and Turner1956) suggest, when extrapolated to a pure plume, a maximum rise of
![]() $Z_{max}=3.79(B_{0}/N^{3})^{1/4}$
and an entrainment coefficient (assuming Gaussian-plume profiles) of 0.093. Translated to the notation of the present paper this implies a maximum height of
$Z_{max}=3.79(B_{0}/N^{3})^{1/4}$
and an entrainment coefficient (assuming Gaussian-plume profiles) of 0.093. Translated to the notation of the present paper this implies a maximum height of
![]() $1.16l_{s}$
. This is extremely close to that cited above for the Gaussian-plume zero-momentum level, suggesting that, despite the deficiencies of the entrainment assumption in the overshoot region, the maximum height of rise,
$1.16l_{s}$
. This is extremely close to that cited above for the Gaussian-plume zero-momentum level, suggesting that, despite the deficiencies of the entrainment assumption in the overshoot region, the maximum height of rise,
![]() $Z_{max}$
, is close to that by direct integration:
$Z_{max}$
, is close to that by direct integration:
![]() $1.15l_{s}$
for Gaussian, or
$1.15l_{s}$
for Gaussian, or
![]() $1.37l_{s}$
for top-hat, plume profiles, respectively.
$1.37l_{s}$
for top-hat, plume profiles, respectively.
The curtain of plume material, being negatively buoyant, falls back around the rising core, entraining some ambient fluid and feeding an intrusion layer where the density matches the surrounds. A model for this has been proposed by Carrazo, Kaminski & Tait (Reference Carrazo, Kaminski and Tait2010), but in the context of negatively buoyant turbulent fountains. However, the available experimental evidence suggests that, for pure plumes, the amount of ambient fluid entrained in the overshoot region is much smaller than that in the rise phase, probably because, unlike forced plumes, relative velocities in this region are smaller and the interface between plume and ambient fluid is stably stratified. For the height of the intrusion layer,
![]() $Z_{T}$
, Richards et al. (Reference Richards, Aubourg and Sutherland2014) cite
$Z_{T}$
, Richards et al. (Reference Richards, Aubourg and Sutherland2014) cite
![]() $Z_{T}=2.7(B_{0}/N^{3})^{1/4}$
for a pure plume. Accepting the maximum rise height
$Z_{T}=2.7(B_{0}/N^{3})^{1/4}$
for a pure plume. Accepting the maximum rise height
![]() $Z_{max}$
in the previous paragraph, this implies
$Z_{max}$
in the previous paragraph, this implies
![]() $Z_{T}/Z_{max}=0.71$
. Mirajkar et al. (Reference Mirajkar, Tirodkar and Balasubramanian2015), with forced plumes, cite similar ratios: 0.68 for single phase, or 0.75 with particle loading, the larger being primarily a consequence of particle re-entrainment depressing the maximum height of rise. The ratio of neutral-buoyancy height to maximum rise height for our naively integrated plume equations is 0.76, not substantially different from these ratios.
$Z_{T}/Z_{max}=0.71$
. Mirajkar et al. (Reference Mirajkar, Tirodkar and Balasubramanian2015), with forced plumes, cite similar ratios: 0.68 for single phase, or 0.75 with particle loading, the larger being primarily a consequence of particle re-entrainment depressing the maximum height of rise. The ratio of neutral-buoyancy height to maximum rise height for our naively integrated plume equations is 0.76, not substantially different from these ratios.
We conclude then that, despite its formal inapplicability in the overshoot (fountain) region, for pure plumes a simple integral plume model is consistent with an initial maximum rise predicted from the zero-momentum level (
![]() $W_{T}=0$
) and an intrusion at the zero-buoyancy level (
$W_{T}=0$
) and an intrusion at the zero-buoyancy level (
![]() $B_{T}=0$
) in the plume. This is unlikely to be true for buoyant jets, since the enhanced momentum is expected to lead to more substantial entrainment in the overshoot region.
$B_{T}=0$
) in the plume. This is unlikely to be true for buoyant jets, since the enhanced momentum is expected to lead to more substantial entrainment in the overshoot region.
2.2 Invariants
Before addressing particle-laden plumes, we note two invariants in special cases.
In an unstratified environment, the last of (2.1) gives constant buoyancy flux:
This is widely used, but not relevant to the stratified environment here.
In a uniformly stratified environment (
![]() $N=\text{const.}$
) the last two equations of (2.8) can be combined and rearranged to give, for the
$N=\text{const.}$
) the last two equations of (2.8) can be combined and rearranged to give, for the
![]() $\unicode[STIX]{x1D6FC}$
-scaled variables:
$\unicode[STIX]{x1D6FC}$
-scaled variables:
Hence, in
![]() $\unicode[STIX]{x1D6FC}$
-scaled variables,
$\unicode[STIX]{x1D6FC}$
-scaled variables,
The corresponding result in dimensional variables is a second (and surprisingly, but as far as we can tell, not hitherto highlighted) invariant
As a corollary, for a pure plume (
![]() $m_{0}=0$
,
$m_{0}=0$
,
![]() $b_{0}=1$
), then at the neutral-buoyancy level (
$b_{0}=1$
), then at the neutral-buoyancy level (
![]() $b=0$
) one must have
$b=0$
) one must have
whilst at maximum rise (
![]() $m=0$
),
$m=0$
),
Thus, if the plume equations were to be integrated to the point of zero vertical velocity then the buoyancy here would be equal and opposite to that at the source (figure 2 a).
2.3 Intrusion layer
The concentration of particles within the spreading intrusion is assumed to be axisymmetric, and the local volumetric flux of particles through the bottom of the intrusion is assumed to be given by fall speed
![]() $W_{s}$
multiplied by particle concentration (figure 1). Assuming, first of all, that there is negligible entrainment of ambient fluid in the overshoot region or the spreading intrusion, the volumetric concentration of particles in the intrusion,
$W_{s}$
multiplied by particle concentration (figure 1). Assuming, first of all, that there is negligible entrainment of ambient fluid in the overshoot region or the spreading intrusion, the volumetric concentration of particles in the intrusion,
![]() $C(r)$
, can be found (Sparks et al.
Reference Sparks, Carey and Sigurdsson1991):
$C(r)$
, can be found (Sparks et al.
Reference Sparks, Carey and Sigurdsson1991):
where
![]() $r$
is radius and
$r$
is radius and
![]() $Q_{T}$
is the volumetric flux in the plume at the intrusion height
$Q_{T}$
is the volumetric flux in the plume at the intrusion height
![]() $Z_{T}$
(hence also the radial volume flux in the intrusion). The solution matching the plume radius
$Z_{T}$
(hence also the radial volume flux in the intrusion). The solution matching the plume radius
![]() $R_{T}$
at the intrusion height is
$R_{T}$
at the intrusion height is
This profile has been used in the past for intrusions forming a free-surface gravity current, as in laboratory studies of plumes injected into unstratified fluid (Sparks et al.
Reference Sparks, Carey and Sigurdsson1991; Veitch & Woods Reference Veitch and Woods2000). However, it assumes that the volume flux entering the intrusion layer is the same as that in the plume just below this layer. For the present, stratification determined, intrusions we can allow for additional particle free, and hence less dense, fluid entrained in the overshoot region. If we suppose an additional volume flux
![]() $\unicode[STIX]{x1D700}Q_{T}$
to be entrained here, then the total volume flux entering the intrusion layer is
$\unicode[STIX]{x1D700}Q_{T}$
to be entrained here, then the total volume flux entering the intrusion layer is
![]() $(1+\unicode[STIX]{x1D700})Q_{T}$
and the initial concentration is
$(1+\unicode[STIX]{x1D700})Q_{T}$
and the initial concentration is
![]() $C_{T}/(1+\unicode[STIX]{x1D700})$
. Equation (2.18) is then amended to read:
$C_{T}/(1+\unicode[STIX]{x1D700})$
. Equation (2.18) is then amended to read:
The fraction
![]() $\unicode[STIX]{x1D700}$
links the buoyancy at the top of the plume,
$\unicode[STIX]{x1D700}$
links the buoyancy at the top of the plume,
![]() $B_{T}$
, and the distance between the maximum height in the fountain and the intrusion level, both of which can, in principle, be parameterised experimentally. If we estimate the averaged entrained density as that in the ambient fluid half-way between these levels and equate the resulting density of plume fluid entering the intrusion to the ambient fluid density at intrusion height then we have, from mass flux divided by volume flux entering the intrusion:
$B_{T}$
, and the distance between the maximum height in the fountain and the intrusion level, both of which can, in principle, be parameterised experimentally. If we estimate the averaged entrained density as that in the ambient fluid half-way between these levels and equate the resulting density of plume fluid entering the intrusion to the ambient fluid density at intrusion height then we have, from mass flux divided by volume flux entering the intrusion:
 $$\begin{eqnarray}\frac{\unicode[STIX]{x1D70C}_{T}Q_{T}+\left(\unicode[STIX]{x1D70C}_{a}(Z_{T})+{\displaystyle \frac{1}{2}}(Z_{max}-Z_{T}){\displaystyle \frac{\text{d}\unicode[STIX]{x1D70C}_{a}}{\text{d}Z}}\right)\unicode[STIX]{x1D700}Q_{T}}{(1+\unicode[STIX]{x1D700})Q_{T}}=\unicode[STIX]{x1D70C}_{a}(Z_{T}),\end{eqnarray}$$
$$\begin{eqnarray}\frac{\unicode[STIX]{x1D70C}_{T}Q_{T}+\left(\unicode[STIX]{x1D70C}_{a}(Z_{T})+{\displaystyle \frac{1}{2}}(Z_{max}-Z_{T}){\displaystyle \frac{\text{d}\unicode[STIX]{x1D70C}_{a}}{\text{d}Z}}\right)\unicode[STIX]{x1D700}Q_{T}}{(1+\unicode[STIX]{x1D700})Q_{T}}=\unicode[STIX]{x1D70C}_{a}(Z_{T}),\end{eqnarray}$$
or, after rearrangement and rewriting in terms of buoyancy flux and buoyancy frequency:
Thus, the height of the intrusion layer
![]() $Z_{T}$
(with corresponding buoyancy
$Z_{T}$
(with corresponding buoyancy
![]() $B_{T}=B(Z_{T})$
) and maximum initial height,
$B_{T}=B(Z_{T})$
) and maximum initial height,
![]() $Z_{max}$
, are intimately related to the additional volume flux entrained,
$Z_{max}$
, are intimately related to the additional volume flux entrained,
![]() $\unicode[STIX]{x1D700}Q_{T}$
. If
$\unicode[STIX]{x1D700}Q_{T}$
. If
![]() $Z_{max}$
and
$Z_{max}$
and
![]() $Z_{T}$
can be determined experimentally, then the ratio,
$Z_{T}$
can be determined experimentally, then the ratio,
![]() $\unicode[STIX]{x1D700}$
, of ambient fluid entrained in the overshoot region to that below the intrusion can be obtained. Conversely, for any given
$\unicode[STIX]{x1D700}$
, of ambient fluid entrained in the overshoot region to that below the intrusion can be obtained. Conversely, for any given
![]() $\unicode[STIX]{x1D700}$
,
$\unicode[STIX]{x1D700}$
,
![]() $Z_{T}$
can be determined numerically from (2.21) and the integral plume solution by noting that the quantity
$Z_{T}$
can be determined numerically from (2.21) and the integral plume solution by noting that the quantity
varies monotonically from positive at the neutral-buoyancy level, to negative at
![]() $Z_{max}$
.
$Z_{max}$
.
In the remainder of the paper we will retain
![]() $\unicode[STIX]{x1D700}$
as a free parameter in order to investigate the effect of the overshoot region. However, we also note the evidence presented at the end of § 2.1, which suggests that, for pure plumes at least,
$\unicode[STIX]{x1D700}$
as a free parameter in order to investigate the effect of the overshoot region. However, we also note the evidence presented at the end of § 2.1, which suggests that, for pure plumes at least,
![]() $B_{T}$
, and hence
$B_{T}$
, and hence
![]() $\unicode[STIX]{x1D700}$
, is nearly 0. This is not the case for buoyant jets, because the experimental evidence cited earlier indicates that the additional momentum increases the initial rise,
$\unicode[STIX]{x1D700}$
, is nearly 0. This is not the case for buoyant jets, because the experimental evidence cited earlier indicates that the additional momentum increases the initial rise,
![]() $Z_{max}$
, and is likely to promote greater mixing in the overshoot region. To highlight the effect that entrainment in the overshoot region could have, we plot graphs of non-dimensional intrusion height (
$Z_{max}$
, and is likely to promote greater mixing in the overshoot region. To highlight the effect that entrainment in the overshoot region could have, we plot graphs of non-dimensional intrusion height (
![]() $Z_{T}/l_{s}$
), intrusion-level plume buoyancy (
$Z_{T}/l_{s}$
), intrusion-level plume buoyancy (
![]() $B_{T}/B_{0}$
) and critical source buoyancy ratio for particles (
$B_{T}/B_{0}$
) and critical source buoyancy ratio for particles (
![]() $P_{crit}$
– see § 2.4 below) against
$P_{crit}$
– see § 2.4 below) against
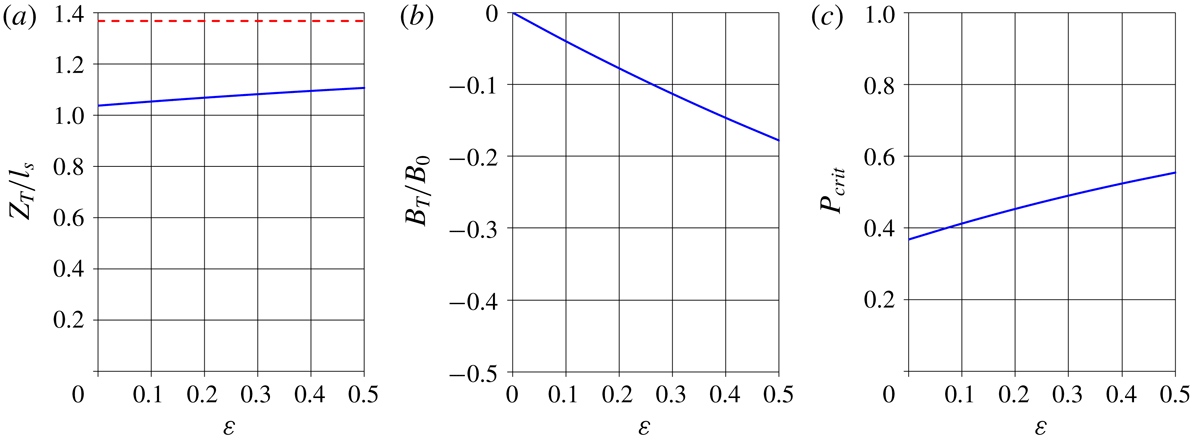
![]() $\unicode[STIX]{x1D700}$
in figure 3. The graphs show that entrainment in the overshoot region will, by entraining slightly lighter fluid, lead to a modest increase in intrusion height
$\unicode[STIX]{x1D700}$
in figure 3. The graphs show that entrainment in the overshoot region will, by entraining slightly lighter fluid, lead to a modest increase in intrusion height
![]() $Z_{T}$
and small negative values of
$Z_{T}$
and small negative values of
![]() $B_{T}$
. But, since the entrained fluid in this region is completely particle free, the effect on
$B_{T}$
. But, since the entrained fluid in this region is completely particle free, the effect on
![]() $P_{crit}$
is more substantial.
$P_{crit}$
is more substantial.

Figure 3. Effect of
![]() $\unicode[STIX]{x1D700}$
(ratio of volume flux entrained in the overshoot region to that at the top of the plume) on (a) non-dimensional intrusion height,
$\unicode[STIX]{x1D700}$
(ratio of volume flux entrained in the overshoot region to that at the top of the plume) on (a) non-dimensional intrusion height,
![]() $Z_{T}/l_{s}$
, with maximum rise
$Z_{T}/l_{s}$
, with maximum rise
![]() $Z_{max}/l_{s}$
shown by the dashed line; (b) non-dimensional plume buoyancy,
$Z_{max}/l_{s}$
shown by the dashed line; (b) non-dimensional plume buoyancy,
![]() $B_{T}/B_{0}$
, at intrusion height; (c) critical source buoyancy ratio
$B_{T}/B_{0}$
, at intrusion height; (c) critical source buoyancy ratio
![]() $P_{crit}$
(see § 2.4).
$P_{crit}$
(see § 2.4).
2.4 Collapse of particle-laden plumes
In cases where the plume source contains particles, these particles will affect the overall total buoyancy. We assume that the total buoyancy is given by
![]() $B=B_{F}+B_{P}$
, where
$B=B_{F}+B_{P}$
, where
![]() $B_{F}$
is the buoyancy flux due to the plume fluid and
$B_{F}$
is the buoyancy flux due to the plume fluid and
![]() $B_{P}$
is the buoyancy flux (assumed negative) due to the particles. We write
$B_{P}$
is the buoyancy flux (assumed negative) due to the particles. We write
for the magnitude of the source buoyancy flux ratio (with
![]() $0\leqslant P<1$
). In many previous studies particles are assumed to have negligible effect on the flow (
$0\leqslant P<1$
). In many previous studies particles are assumed to have negligible effect on the flow (
![]() $P\ll 1$
), but we make no such assumption here. In this section (but not for our more detailed model in § 3) we assume that the rising plume is sufficiently strong that particles remain within the plume until it begins to spread as an intrusion.
$P\ll 1$
), but we make no such assumption here. In this section (but not for our more detailed model in § 3) we assume that the rising plume is sufficiently strong that particles remain within the plume until it begins to spread as an intrusion.
Particles fall at their settling velocity,
![]() $W_{s}$
, through the ambient fluid. As they fall they are drawn towards the rising plume and those that fall from the intrusion at less than a critical radius
$W_{s}$
, through the ambient fluid. As they fall they are drawn towards the rising plume and those that fall from the intrusion at less than a critical radius
![]() $R_{c}$
are re-entrained rather than falling to the floor. To calculate
$R_{c}$
are re-entrained rather than falling to the floor. To calculate
![]() $R_{c}$
it is necessary to integrate the effect of the horizontal entrainment of the particles toward the plume centre line as the particles descend. Such an analytical approximation to the critical radius has been described by Sparks et al. (Reference Sparks, Carey and Sigurdsson1991), Lane-Serff (Reference Lane-Serff1995) and Mingotti & Woods (Reference Mingotti and Woods2015) for a linearly stratified ambient medium. By contrast, our formulation here, which was derived independently but turns out to be a rephrased version of that in Veitch & Woods (Reference Veitch and Woods2000), avoids making assumptions about the ambient stratification or the vertical profile of plume radius or entrainment velocity.
$R_{c}$
it is necessary to integrate the effect of the horizontal entrainment of the particles toward the plume centre line as the particles descend. Such an analytical approximation to the critical radius has been described by Sparks et al. (Reference Sparks, Carey and Sigurdsson1991), Lane-Serff (Reference Lane-Serff1995) and Mingotti & Woods (Reference Mingotti and Woods2015) for a linearly stratified ambient medium. By contrast, our formulation here, which was derived independently but turns out to be a rephrased version of that in Veitch & Woods (Reference Veitch and Woods2000), avoids making assumptions about the ambient stratification or the vertical profile of plume radius or entrainment velocity.

Figure 4. Re-entrainment region and particle fluxes.
The ‘entrainment boundary’ distinguishing falling particles which may be re-entrained into the plume from those which escape to be deposited on the ground (figure 4) may be computed from a particle velocity given in radial/vertical coordinates by
 $$\begin{eqnarray}\boldsymbol{U}=\left(\begin{array}{@{}c@{}}-{\displaystyle \frac{V_{e}R}{r}}\\ -W_{s}\end{array}\right),\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{U}=\left(\begin{array}{@{}c@{}}-{\displaystyle \frac{V_{e}R}{r}}\\ -W_{s}\end{array}\right),\end{eqnarray}$$
where
![]() $V_{e}$
is the entrainment velocity,
$V_{e}$
is the entrainment velocity,
![]() $r$
is the local radial coordinate and
$r$
is the local radial coordinate and
![]() $R$
is the plume radius at that height. Then
$R$
is the plume radius at that height. Then
or
i.e.
Hence, for a pure plume with
![]() $r=Q=0$
at source:
$r=Q=0$
at source:
The critical radius
![]() $R_{c}$
at intrusion height
$R_{c}$
at intrusion height
![]() $Z_{T}$
is given by
$Z_{T}$
is given by
where
![]() $W_{T}$
is the upward velocity in the plume at this level. Note that this critical radius depends only on the flow field generated by the plume below the intrusion and not on fluid entrained in the overshoot (except, indirectly, in so far as that may affect the intrusion height). This equation is equally valid in free-surface-limited and stratification-limited cases.
$W_{T}$
is the upward velocity in the plume at this level. Note that this critical radius depends only on the flow field generated by the plume below the intrusion and not on fluid entrained in the overshoot (except, indirectly, in so far as that may affect the intrusion height). This equation is equally valid in free-surface-limited and stratification-limited cases.
In the intrusion layer, then, equation (2.19) can be written
and the proportion of particulate re-entrained is, with F the advective flux of particulate:
In particular, if the particle settling velocity is small (
![]() $W_{s}/W_{T}\ll 1$
, or
$W_{s}/W_{T}\ll 1$
, or
![]() $R_{T}/R_{c}\ll 1$
) then the proportion re-entrained is
$R_{T}/R_{c}\ll 1$
) then the proportion re-entrained is
If there is no entrainment from the fountain,
![]() $\unicode[STIX]{x1D700}=0$
, and this gives the proportion 0.632 derived by Veitch & Woods (Reference Veitch and Woods2000). A key feature is that this is independent of plume buoyancy, background stratification or particle settling velocity (provided the last is small).
$\unicode[STIX]{x1D700}=0$
, and this gives the proportion 0.632 derived by Veitch & Woods (Reference Veitch and Woods2000). A key feature is that this is independent of plume buoyancy, background stratification or particle settling velocity (provided the last is small).
Equation (2.32) plays a critical role in establishing conditions for plume collapse. We show below that the critical source buoyancy ratio,
![]() $P_{crit}$
is related to the residual buoyancy flux
$P_{crit}$
is related to the residual buoyancy flux
![]() $B_{T}$
in the plume at the height of the intrusion, which, as shown in § 2.3, is related in turn to the amount of entrainment of particle-free fluid in the overshoot region.
$B_{T}$
in the plume at the height of the intrusion, which, as shown in § 2.3, is related in turn to the amount of entrainment of particle-free fluid in the overshoot region.
Consider first the particle flux
![]() $F$
in plume or intrusion (figure 4). For heavy particles,
$F$
in plume or intrusion (figure 4). For heavy particles,
![]() $F$
is proportional to particle buoyancy flux
$F$
is proportional to particle buoyancy flux
![]() $B_{P}$
. Following re-entrainment, a particle flux
$B_{P}$
. Following re-entrainment, a particle flux
![]() $F_{0}$
at source gives rise to a different particle flux
$F_{0}$
at source gives rise to a different particle flux
![]() $F_{T}$
at the top of the plume (i.e. intrusion level). Flux
$F_{T}$
at the top of the plume (i.e. intrusion level). Flux
![]() $\unicode[STIX]{x1D6F7}F_{T}$
is recycled into the plume by re-entrainment, whilst
$\unicode[STIX]{x1D6F7}F_{T}$
is recycled into the plume by re-entrainment, whilst
![]() $(1-\unicode[STIX]{x1D6F7})F_{T}$
escapes. In steady state the latter balances the source flux, so
$(1-\unicode[STIX]{x1D6F7})F_{T}$
escapes. In steady state the latter balances the source flux, so
or, in terms of particle buoyancy,
where subscripts
![]() $T$
and 0 refer to top and source, subscripts
$T$
and 0 refer to top and source, subscripts
![]() $P$
and
$P$
and
![]() $F$
to particle and fluid.
$F$
to particle and fluid.
Now consider the total plume buoyancy (fluid
![]() $+$
particles) at the intrusion level:
$+$
particles) at the intrusion level:
i.e.
At source, by definition of the source buoyancy ratio,
Substituting (2.37) in (2.36) gives
The first bracketed term on the right-hand side is negative (since the plume entrains denser fluid), but becomes zero when the plume collapses (since then the ‘top’
![]() $T$
is at the ground, 0). The critical value of
$T$
is at the ground, 0). The critical value of
![]() $P$
is then given, after rearrangement, by
$P$
is then given, after rearrangement, by
where
![]() $B_{T}\;({\leqslant}0)$
is the plume buoyancy at the height of the intrusion layer and
$B_{T}\;({\leqslant}0)$
is the plume buoyancy at the height of the intrusion layer and
![]() $\unicode[STIX]{x1D6F7}^{\prime }=1-\unicode[STIX]{x1D6F7}$
is the non-entrained fraction. These are, in turn, related via the volume fraction
$\unicode[STIX]{x1D6F7}^{\prime }=1-\unicode[STIX]{x1D6F7}$
is the non-entrained fraction. These are, in turn, related via the volume fraction
![]() $\unicode[STIX]{x1D700}$
entrained in the overshoot region, equations (2.21) and (2.32).
$\unicode[STIX]{x1D700}$
entrained in the overshoot region, equations (2.21) and (2.32).
![]() $P_{crit}$
is plotted as a function of
$P_{crit}$
is plotted as a function of
![]() $\unicode[STIX]{x1D700}$
in figure 3(c).
$\unicode[STIX]{x1D700}$
in figure 3(c).
The minimum height that we might conceivably assign to the spreading layer is the neutral-buoyancy height,
![]() $B_{T}=0$
, occurring when
$B_{T}=0$
, occurring when
![]() $\unicode[STIX]{x1D700}=0$
. Then we have a minimum value of
$\unicode[STIX]{x1D700}=0$
. Then we have a minimum value of
![]() $P_{crit}$
for plume collapse:
$P_{crit}$
for plume collapse:
We conclude that the plume will not collapse for any source buoyancy ratio smaller than this. Moreover, as explained at the end of § 2.3, this is likely to be the critical buoyancy ratio for pure plumes. We will show in § 3 that this bound is consistent with a more detailed computational model.
For buoyant jets, however, the situation is more complex, as the greater momentum throughout is expected to lead to both greater initial rise (Mirajkar et al.
Reference Mirajkar, Tirodkar and Balasubramanian2015) and more mixing with particle-free fluid in the overshoot region. Equations (2.28)–(2.32) require correction for a finite source, whilst
![]() $\unicode[STIX]{x1D6F7}^{\prime }$
and
$\unicode[STIX]{x1D6F7}^{\prime }$
and
![]() $B_{T}$
must be modified. If the source is not large and the change to
$B_{T}$
must be modified. If the source is not large and the change to
![]() $Z_{max}$
is not substantial, then figure 3(c) shows the anticipated change in
$Z_{max}$
is not substantial, then figure 3(c) shows the anticipated change in
![]() $P_{crit}$
with the entrained fraction from the overshoot region,
$P_{crit}$
with the entrained fraction from the overshoot region,
![]() $\unicode[STIX]{x1D700}$
. This paper will primarily focus on pure plumes, but will investigate the effect of overshoot-region entrainment in § 3.5.
$\unicode[STIX]{x1D700}$
. This paper will primarily focus on pure plumes, but will investigate the effect of overshoot-region entrainment in § 3.5.
2.5 Effect of particle sedimentation on the intrusion layer
In response to a reviewer’s comment, we address the effect on the intrusion layer of its particle load being continually diminished by sedimentation. As particles drop out, the overall density of the intrusion would be reduced, potentially leading to a layer that was not horizontal but increased in height with radius.
To our knowledge this has never been observed experimentally. Any buoyant tendency to rise would promote entrainment that quickly restored the neutral buoyancy of the layer, albeit thickening it. Even if there were a resultant rise then, in the region below the base of the intrusion, but above the original intrusion height, there would be no horizontal entrainment into the rising plume, and so particles would drop vertically until they reached the original intrusion height. Thus, apart from a small extra fall time, there is no significant effect on the re-entrainment process, and the model of § 2.4 (where we assumed a horizontal intrusion) will give the correct results for the recycled fraction, at least for a quasi-steady flow.
Even if no entrainment into the intrusion took place and it rose with radius, we can place an upper bound on any rise at the critical radius (the maximum distance at which it can have any effect on the re-entraining part of the flow). Any entrainment in the overshoot region inevitably dilutes the particle concentration. Hence, the maximum effect of particle dropout on intrusion density will occur if the intrusion height
![]() $Z_{T}$
is where the plume first reaches overall neutral buoyancy,
$Z_{T}$
is where the plume first reaches overall neutral buoyancy,
![]() $B_{T}=0$
, In this case we have
$B_{T}=0$
, In this case we have
![]() $B_{T}^{(F)}=-B_{T}^{(P)}$
. At the critical radius, the particle buoyancy in the intrusion is the same as that at the source,
$B_{T}^{(F)}=-B_{T}^{(P)}$
. At the critical radius, the particle buoyancy in the intrusion is the same as that at the source,
![]() $B_{0}^{(P)}$
. Thus, the buoyancy in the intrusion at the critical radius is (see (2.34) and (2.37)):
$B_{0}^{(P)}$
. Thus, the buoyancy in the intrusion at the critical radius is (see (2.34) and (2.37)):
At
![]() $P=P_{crit}$
this is just
$P=P_{crit}$
this is just
![]() $B_{0}$
. The density contrast is proportional to the buoyancy divided by the volume flow rate. The height the intrusion needs to rise to match the ambient density in this case is then (in
$B_{0}$
. The density contrast is proportional to the buoyancy divided by the volume flow rate. The height the intrusion needs to rise to match the ambient density in this case is then (in
![]() $\unicode[STIX]{x1D6FC}$
-scaled units)
$\unicode[STIX]{x1D6FC}$
-scaled units)
![]() $z_{rise}=1/q_{T}$
, where
$z_{rise}=1/q_{T}$
, where
![]() $q_{T}=2.49$
is the non-dimensional volume flux where the plume reaches neutral density, and thus
$q_{T}=2.49$
is the non-dimensional volume flux where the plume reaches neutral density, and thus
![]() $z_{rise}=0.402$
(compared with an initial non-dimensional intrusion height
$z_{rise}=0.402$
(compared with an initial non-dimensional intrusion height
![]() $z_{T}=1.038$
). Initial particle loads below the critical value will lead to smaller changes in intrusion height.
$z_{T}=1.038$
). Initial particle loads below the critical value will lead to smaller changes in intrusion height.
We reiterate that we do not expect the rise to happen, and that, even if it did, it would have no effect on the criterion for plume collapse and a very minor effect on the time to collapse.
2.6 Time to collapse
The entrainment of particles into the plume reduces the overall buoyancy of the rising plume and depresses the intrusion height from its initial value. The intrusion height will tend to a steady non-zero value if
![]() $P$
is smaller than the critical value, while the intrusion height will reach zero in a finite time for values of
$P$
is smaller than the critical value, while the intrusion height will reach zero in a finite time for values of
![]() $P$
larger than the critical value. We can estimate the change in intrusion height by estimating the overall change in buoyancy flux (since the heights scale with the quarter power of the buoyancy flux) while the time scale for the recycling process depends mostly on the fall time (which is much longer than the rise time in the plume or spreading time in the intrusion). The fall time is given by the intrusion height divided by the fall speed and diminishes as the intrusion height diminishes.
$P$
larger than the critical value. We can estimate the change in intrusion height by estimating the overall change in buoyancy flux (since the heights scale with the quarter power of the buoyancy flux) while the time scale for the recycling process depends mostly on the fall time (which is much longer than the rise time in the plume or spreading time in the intrusion). The fall time is given by the intrusion height divided by the fall speed and diminishes as the intrusion height diminishes.
In a simple model we imagine successive discrete particle-recycling events, occurring at the time intervals over which a particle falls with velocity
![]() $W_{s}$
a distance equal to the varying intrusion height
$W_{s}$
a distance equal to the varying intrusion height
![]() $Z_{T}$
. The particulate contribution to buoyancy at the top of the plume after
$Z_{T}$
. The particulate contribution to buoyancy at the top of the plume after
![]() $n$
recycling events is (cf. (2.34)):
$n$
recycling events is (cf. (2.34)):
Since the particle flux is added to the plume throughout its height, it is not straightforward to use the flux at source in an estimate of the changing intrusion height. However, the following is consistent with the requirements that: (i) the intrusion height
![]() $Z_{T}^{(n)}$
scales (in some sense) as (buoyancy)
$Z_{T}^{(n)}$
scales (in some sense) as (buoyancy)
![]() $^{1/4}$
; and (ii)
$^{1/4}$
; and (ii)
![]() $Z_{T}^{(n)}\rightarrow 0$
as
$Z_{T}^{(n)}\rightarrow 0$
as
![]() $n\rightarrow \infty$
for plumes that just collapse:
$n\rightarrow \infty$
for plumes that just collapse:
If we take the case of
![]() $B_{T}=0$
in (2.43) this gives intrusion heights that are the same as those predicted by injecting all the buoyancy flux from the entrained particles at the source, corresponding to the quickest collapse or lowest final intrusion height.
$B_{T}=0$
in (2.43) this gives intrusion heights that are the same as those predicted by injecting all the buoyancy flux from the entrained particles at the source, corresponding to the quickest collapse or lowest final intrusion height.
Using (2.37) for
![]() $B_{0,F}$
and
$B_{0,F}$
and
![]() $B_{0,P}$
, equation (2.39) for
$B_{0,P}$
, equation (2.39) for
![]() $B_{T}$
, and (2.42) for
$B_{T}$
, and (2.42) for
![]() $B_{T.P}^{(n)}$
:
$B_{T.P}^{(n)}$
:
where, with
![]() $P_{crit}$
the critical source buoyancy ratio for collapse given by (2.39),
$P_{crit}$
the critical source buoyancy ratio for collapse given by (2.39),
 $$\begin{eqnarray}\unicode[STIX]{x1D707}=\frac{1-{\displaystyle \frac{P_{crit}}{P}}}{1-P_{crit}}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D707}=\frac{1-{\displaystyle \frac{P_{crit}}{P}}}{1-P_{crit}}.\end{eqnarray}$$
Consider first the marginal case where the plume just collapses:
![]() $P=P_{crit}$
or
$P=P_{crit}$
or
![]() $\unicode[STIX]{x1D707}=0$
, and
$\unicode[STIX]{x1D707}=0$
, and
This appears to approach
![]() $Z_{T}^{(n)}=0$
asymptotically. However, as the fall time is reduced at each recycling, complete collapse is actually obtained in finite time. Summing the first
$Z_{T}^{(n)}=0$
asymptotically. However, as the fall time is reduced at each recycling, complete collapse is actually obtained in finite time. Summing the first
![]() $n$
recyclings, with fall time during the
$n$
recyclings, with fall time during the
![]() $n$
th recycling,
$n$
th recycling,
![]() $\unicode[STIX]{x0394}t^{(n)}=Z_{T}^{(n-1)}/W_{s}$
:
$\unicode[STIX]{x0394}t^{(n)}=Z_{T}^{(n-1)}/W_{s}$
:
Rearranging for
![]() $\unicode[STIX]{x1D6F7}^{n/4}$
and substituting in (2.46) gives for the intrusion height
$\unicode[STIX]{x1D6F7}^{n/4}$
and substituting in (2.46) gives for the intrusion height
![]() $Z_{T}$
:
$Z_{T}$
:
With
![]() $\unicode[STIX]{x1D6F7}=0.632$
this gives an estimate of time to collapse for the marginal case as
$\unicode[STIX]{x1D6F7}=0.632$
this gives an estimate of time to collapse for the marginal case as
Equations (2.44) and (2.45) confirm that if
![]() $P<P_{crit}\;(\unicode[STIX]{x1D707}<0)$
there is no collapse, whereas if
$P<P_{crit}\;(\unicode[STIX]{x1D707}<0)$
there is no collapse, whereas if
![]() $P>P_{crit}\;(\unicode[STIX]{x1D707}>0)$
plume collapse is faster than the critical case.
$P>P_{crit}\;(\unicode[STIX]{x1D707}>0)$
plume collapse is faster than the critical case.
In the non-collapsing case (
![]() $\unicode[STIX]{x1D707}<0$
) the model produces an estimate of the ratio of final to initial intrusion height:
$\unicode[STIX]{x1D707}<0$
) the model produces an estimate of the ratio of final to initial intrusion height:
In the collapsing case, with
![]() $P>P_{crit}$
, the time to collapse can be estimated by summing (numerically) fall times
$P>P_{crit}$
, the time to collapse can be estimated by summing (numerically) fall times
![]() $\unicode[STIX]{x0394}t^{(n)}=Z_{T}^{(n-1)}/W_{s}$
. This depends on
$\unicode[STIX]{x0394}t^{(n)}=Z_{T}^{(n-1)}/W_{s}$
. This depends on
![]() $P_{crit}$
, which is determined from the volume fraction
$P_{crit}$
, which is determined from the volume fraction
![]() $\unicode[STIX]{x1D700}$
entrained in the overshoot region via the re-entrained particulate fraction
$\unicode[STIX]{x1D700}$
entrained in the overshoot region via the re-entrained particulate fraction
![]() $\unicode[STIX]{x1D6F7}$
and residual buoyancy ratio
$\unicode[STIX]{x1D6F7}$
and residual buoyancy ratio
![]() $B_{T}/B_{0}$
((2.21), (2.32), (2.39); figure 3). Typical behaviour is illustrated in figure 5. Collapse time increases markedly near the critical value of
$B_{T}/B_{0}$
((2.21), (2.32), (2.39); figure 3). Typical behaviour is illustrated in figure 5. Collapse time increases markedly near the critical value of
![]() $P$
, but does not exceed the limiting values from (2.48) for each value of
$P$
, but does not exceed the limiting values from (2.48) for each value of
![]() $\unicode[STIX]{x1D6F7}$
.
$\unicode[STIX]{x1D6F7}$
.
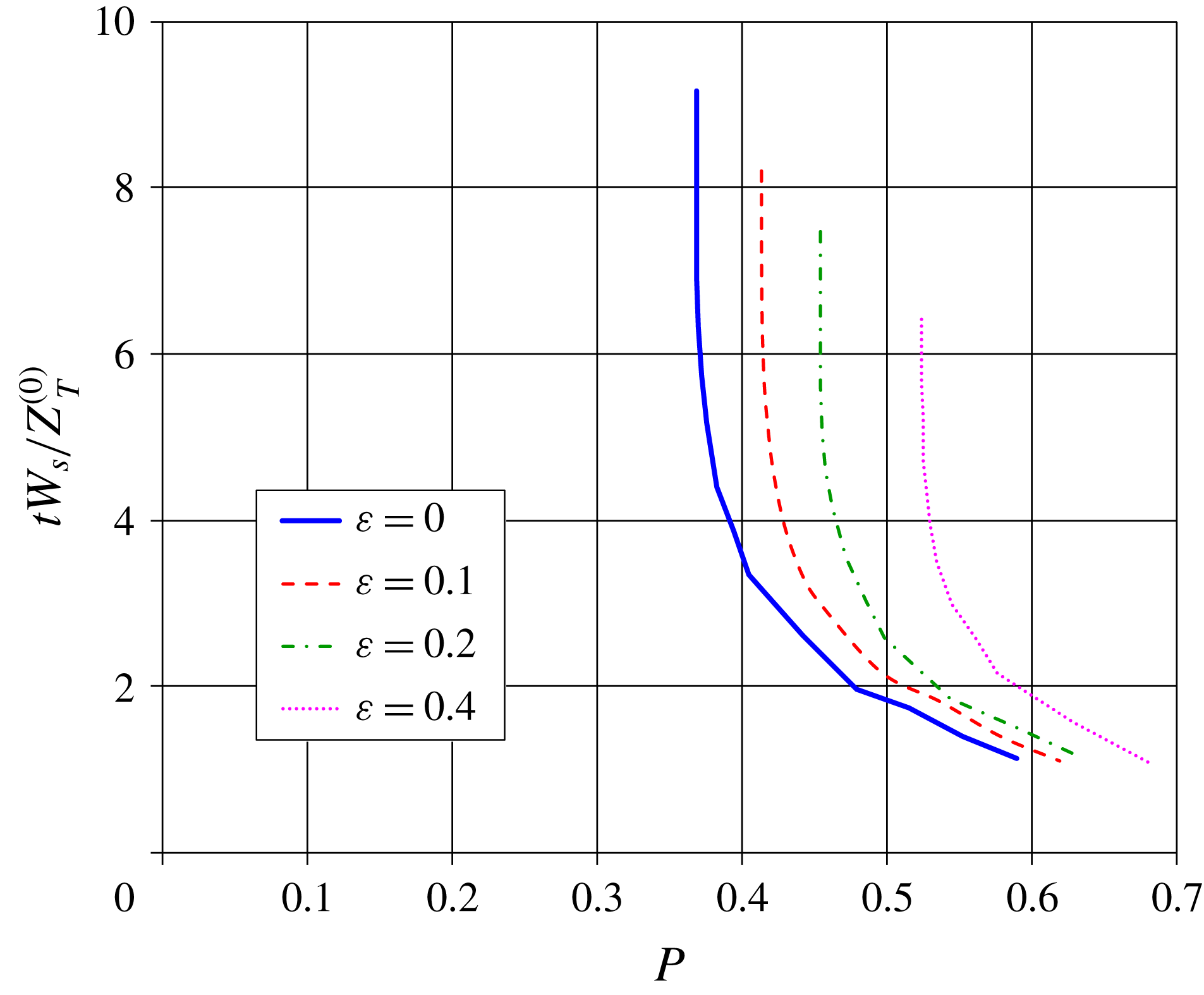
Figure 5. Time to collapse versus source buoyancy ratio
![]() $P$
for different degrees of entrainment in the overshoot region.
$P$
for different degrees of entrainment in the overshoot region.
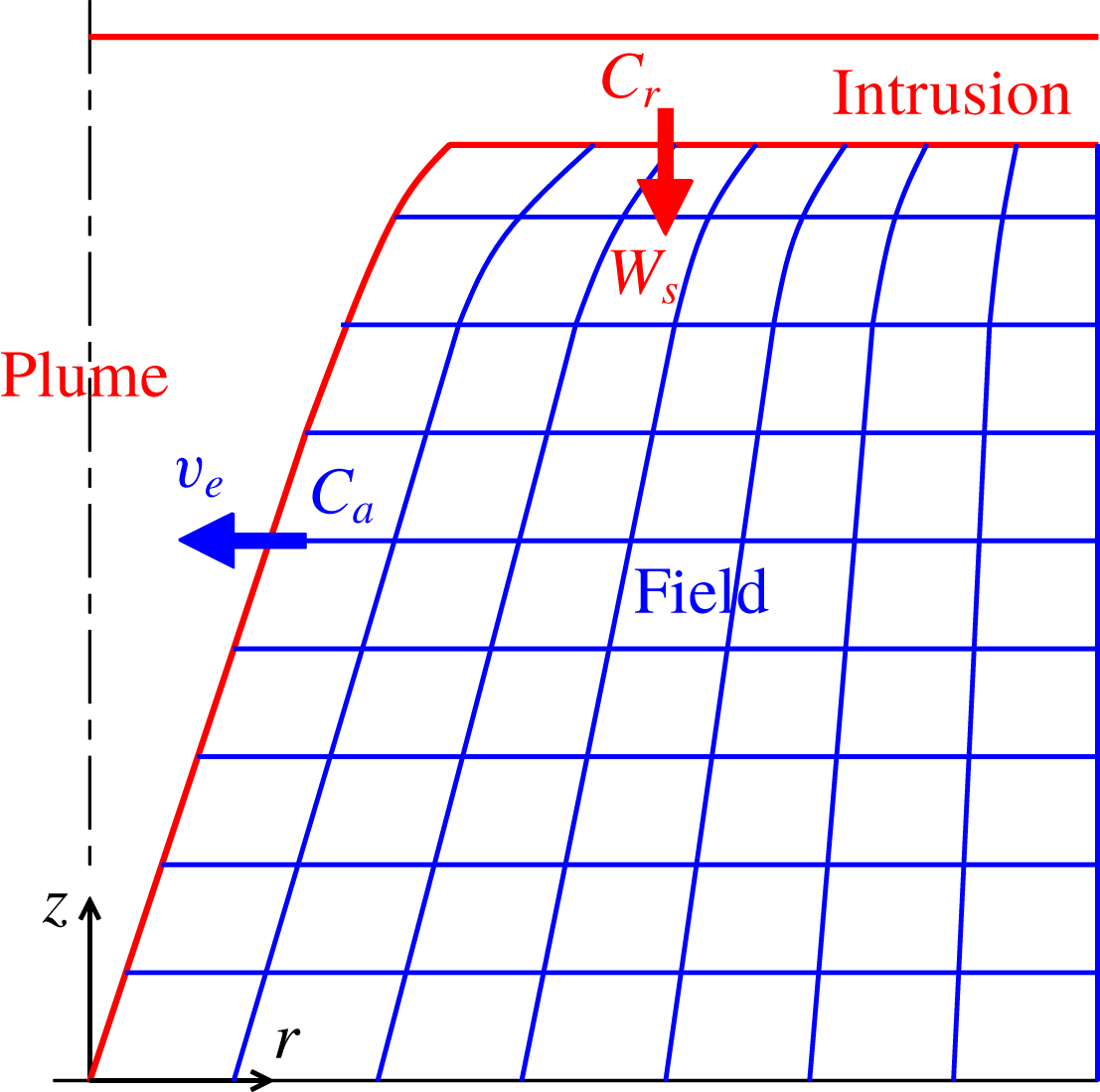
Figure 6. Schematic of PLUME and FIELD regions.
This idealised model makes the assumption that individual recycling events occur at discrete time intervals
![]() $Z_{T}^{(n)}/W_{s}$
, whereas, in reality, particles are re-entrained continuously in time over the full depth of the plume, the greatest particle re-entrainment occurring (at the shortest time interval) near the top of the plume. An advanced model seeks to provide a more accurate picture of events in § 3 below.
$Z_{T}^{(n)}/W_{s}$
, whereas, in reality, particles are re-entrained continuously in time over the full depth of the plume, the greatest particle re-entrainment occurring (at the shortest time interval) near the top of the plume. An advanced model seeks to provide a more accurate picture of events in § 3 below.
3 Numerical model of concentration evolution
3.1 Overview
A computational model has been developed to supplement the simple analytical modelling in § 2. This advanced model offers several major advantages over the simple model of § 2; it enables the temporal evolution of plume and particle cloud to be followed, including the time to collapse; it incorporates time-dependent changes to plume density due to particulate re-entrainment; for heavier particles it can accommodate fallout from the plume during the rise phase. (Although not tested here, it would also admit an arbitrary ambient density profile.)
The model has two components (figure 6): a PLUME component consisting of an integral plume model and a horizontal intrusion, where plume rise is limited by ambient stratification; and a FIELD component where a time-dependent advection equation is solved by a two-dimensional, axisymmetric finite-volume approach for the concentration of particulate material falling out of the horizontal layer and being partially re-entrained into the plume.
These two components are coupled. The PLUME model supplies plume radius as a function of height, as well as the height of the spreading horizontal layer, the entrainment velocity at the plume boundary (which determines the horizontal velocity field outside) and the concentration distribution in the horizontal layer (2.19). The time-dependent FIELD model supplies the ambient concentration at the plume boundary, which is used to determine entrainment of particulate into the plume.
Assuming plume rise velocities to be much larger than particle settling velocity, it is sufficient that within each time step there be a single update of the quasi-static integral PLUME equations with current ambient conditions of density and concentration, followed by an update of the FIELD component.
3.2 PLUME model
In this section, the following integral plume equations are solved for volume flux
![]() $Q$
, specific momentum flux
$Q$
, specific momentum flux
![]() $M=WQ$
, mass flux
$M=WQ$
, mass flux
![]() ${\dot{m}}=\unicode[STIX]{x1D70C}Q$
and particle volume flux
${\dot{m}}=\unicode[STIX]{x1D70C}Q$
and particle volume flux
![]() $F=CQ$
:
$F=CQ$
:
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}{\displaystyle \frac{\text{d}Q}{\text{d}Z}}=E,\\ {\displaystyle \frac{\text{d}M}{\text{d}Z}}=g^{\prime }A,\\ {\displaystyle \frac{\text{d}{\dot{m}}}{\text{d}Z}}=\unicode[STIX]{x1D70C}_{a}E,\\ {\displaystyle \frac{\text{d}F}{\text{d}Z}}=C_{b}E^{\prime }.\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}{\displaystyle \frac{\text{d}Q}{\text{d}Z}}=E,\\ {\displaystyle \frac{\text{d}M}{\text{d}Z}}=g^{\prime }A,\\ {\displaystyle \frac{\text{d}{\dot{m}}}{\text{d}Z}}=\unicode[STIX]{x1D70C}_{a}E,\\ {\displaystyle \frac{\text{d}F}{\text{d}Z}}=C_{b}E^{\prime }.\end{array}\right\}\end{eqnarray}$$
Here,
![]() $E$
is the entrainment rate, given by
$E$
is the entrainment rate, given by
and other quantities in the first two equations are as in § 2.
In the third equation we solve for the mass flux
![]() ${\dot{m}}=\unicode[STIX]{x1D70C}Q$
, rather than the buoyancy flux
${\dot{m}}=\unicode[STIX]{x1D70C}Q$
, rather than the buoyancy flux
![]() $B$
used in § 2. These are related by
$B$
used in § 2. These are related by
We solve for mass flux rather than buoyancy flux in this section because it is computationally more tractable and permits the surrounding particulate concentration to change the density of entrained material,
![]() $\unicode[STIX]{x1D70C}_{a}$
.
$\unicode[STIX]{x1D70C}_{a}$
.
In the last of (3.1) the net entrainment of heavy particles is, for consistency with the treatment at the boundary of the FIELD region, adjusted for the tendency to fall out of the plume:
and the boundary value
![]() $C_{b}$
is given by
$C_{b}$
is given by
Finally, we note that, since
![]() $A=Q^{2}/M$
, it is computationally advantageous to avoid division by zero by solving the second of (3.1) for
$A=Q^{2}/M$
, it is computationally advantageous to avoid division by zero by solving the second of (3.1) for
![]() $M^{2}$
rather than
$M^{2}$
rather than
![]() $M$
:
$M$
:
With these qualifications, the system of (3.1) is written in vector form as
and solved by the second-order implicit Euler method:
The height of the horizontal intrusion is determined as in § 2.3, following (2.21). It is formally a function of the ratio,
![]() $\unicode[STIX]{x1D700}$
, of the volume of fluid entrained in the overshoot region to that below the intrusion; however, the majority of calculations to be reported here use
$\unicode[STIX]{x1D700}$
, of the volume of fluid entrained in the overshoot region to that below the intrusion; however, the majority of calculations to be reported here use
![]() $\unicode[STIX]{x1D700}=0$
(corresponding to
$\unicode[STIX]{x1D700}=0$
(corresponding to
![]() $B_{T}=0$
), with an examination of the effect of above-intrusion entrainment in § 3.5.
$B_{T}=0$
), with an examination of the effect of above-intrusion entrainment in § 3.5.
Although quasi-static, the plume equations have to be solved afresh at each time step as the ambient particulate concentration changes and affects the overall density of material entrained into the plume:
where
![]() $\unicode[STIX]{x1D70C}_{a,F}$
is the ambient fluid density,
$\unicode[STIX]{x1D70C}_{a,F}$
is the ambient fluid density,
![]() $\unicode[STIX]{x1D70C}_{P}$
is particle density and
$\unicode[STIX]{x1D70C}_{P}$
is particle density and
![]() $C_{a}$
is the ambient concentration (by volume). The last is supplied at the plume boundary by the FIELD model.
$C_{a}$
is the ambient concentration (by volume). The last is supplied at the plume boundary by the FIELD model.
For the integral plume calculation we used a step size
![]() $\unicode[STIX]{x0394}z/L_{s}=0.0005$
, which was found to be adequate for grid-independent solutions for an isolated plume. Integration was carried out to the height of zero rise velocity, beyond that necessary for the intrusion height.
$\unicode[STIX]{x0394}z/L_{s}=0.0005$
, which was found to be adequate for grid-independent solutions for an isolated plume. Integration was carried out to the height of zero rise velocity, beyond that necessary for the intrusion height.
3.3 FIELD model
In the FIELD model a time-dependent axisymmetric finite-volume approach, with curvilinear grid, is used to calculate concentration in the region external to the plume:
The mesh (shown schematically in figure 6) is delimited by the plume boundary, the intrusion layer (whose height may change with time), an outer boundary (fixed, by trial, at the greater of
![]() $10L_{s}$
and the critical radius) and the ground. Dimensions, determined by grid-independence checks in collapsing and non-collapsing cases, was
$10L_{s}$
and the critical radius) and the ground. Dimensions, determined by grid-independence checks in collapsing and non-collapsing cases, was
![]() $800\times 80$
(horizontal
$800\times 80$
(horizontal
![]() $\times$
vertical), with uniform distribution along each horizontal and near-vertical line.
$\times$
vertical), with uniform distribution along each horizontal and near-vertical line.
The relative velocity field of particulate material is determined by the entrainment velocity at the plume boundary
![]() $R$
(but falling off as
$R$
(but falling off as
![]() $1/r$
) and the settling velocity of particles:
$1/r$
) and the settling velocity of particles:
 $$\begin{eqnarray}\left(\begin{array}{@{}c@{}}U_{r}\\ U_{Z}\end{array}\right)=\left(\begin{array}{@{}c@{}}-V_{e}(z){\displaystyle \frac{R(z)}{r}}\\ -W_{s}\end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}\left(\begin{array}{@{}c@{}}U_{r}\\ U_{Z}\end{array}\right)=\left(\begin{array}{@{}c@{}}-V_{e}(z){\displaystyle \frac{R(z)}{r}}\\ -W_{s}\end{array}\right).\end{eqnarray}$$
The small downward velocity of cell faces as the intrusion layer descends could be included in a ‘moving-grid’ approach. However, this is considered sufficiently small here to be neglected. It does not affect the end state.
Dirichlet boundary conditions are supplied at inflow boundaries:
To maintain conservation and for consistency with the plume model (3.4) and (3.5), where there is net positive particle inflow
![]() $E^{\prime }$
to the plume zero-gradient boundary conditions are applied to the FIELD region at the plume boundary and supply the ‘ambient’ concentration
$E^{\prime }$
to the plume zero-gradient boundary conditions are applied to the FIELD region at the plume boundary and supply the ‘ambient’ concentration
![]() $C_{a}$
; conversely, where, due to significant fallout, there is net efflux from the plume this switches locally to Dirichlet conditions, with boundary concentrations those in the plume. At the ground, Neumann boundary condition conditions give the deposition flux.
$C_{a}$
; conversely, where, due to significant fallout, there is net efflux from the plume this switches locally to Dirichlet conditions, with boundary concentrations those in the plume. At the ground, Neumann boundary condition conditions give the deposition flux.
Equation (3.10) is solved for cell-centre concentrations by a standard iterative approach (alternating direction implicit, with tridiagonal solver along coordinate lines), using first-order upwinding for advection and backward differencing for the time derivatives. With these schemes the system of algebraic equations is very diagonally dominant and converges within a few iterations at each time step. Typical computation times (up to a constant final-layer height or complete collapse) were a few minutes on a desktop PC, longest times being required for source buoyancy ratios near the critical value.
3.4 Results
Calculations were carried out for the ‘pure plume’, constant-buoyancy-frequency scenario of § 2. This idealised case (source
![]() $Q=0$
,
$Q=0$
,
![]() $M=0$
,
$M=0$
,
![]() $B_{0}=1$
,
$B_{0}=1$
,
![]() $N=1$
, in units scaled by source buoyancy and buoyancy frequency) is realised computationally by computing source fluxes from a virtual source just below ground level. The results in this section employ a varying particle-to-fluid source buoyancy ratio
$N=1$
, in units scaled by source buoyancy and buoyancy frequency) is realised computationally by computing source fluxes from a virtual source just below ground level. The results in this section employ a varying particle-to-fluid source buoyancy ratio
![]() $P$
(2.23). In this subsection, the height of the horizontal intrusion is taken to be that for which entrainment of particle-free fluid in the overshoot region is negligible,
$P$
(2.23). In this subsection, the height of the horizontal intrusion is taken to be that for which entrainment of particle-free fluid in the overshoot region is negligible,
![]() $\unicode[STIX]{x1D700}\approx 0$
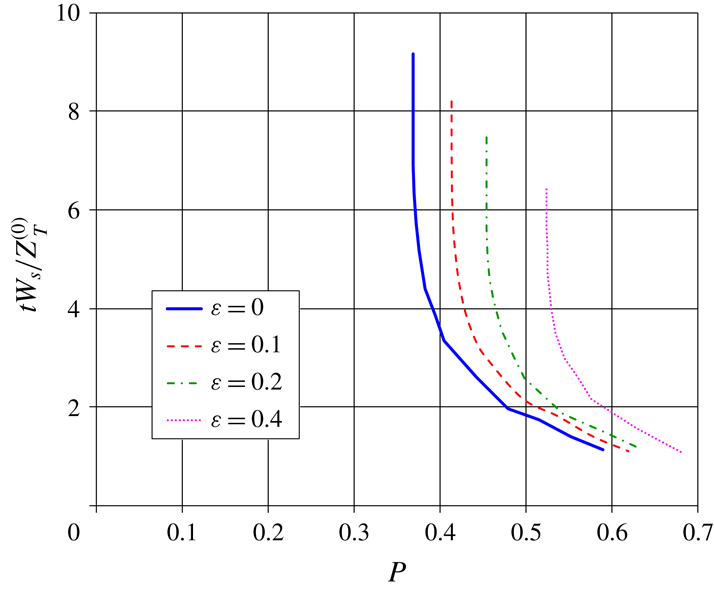
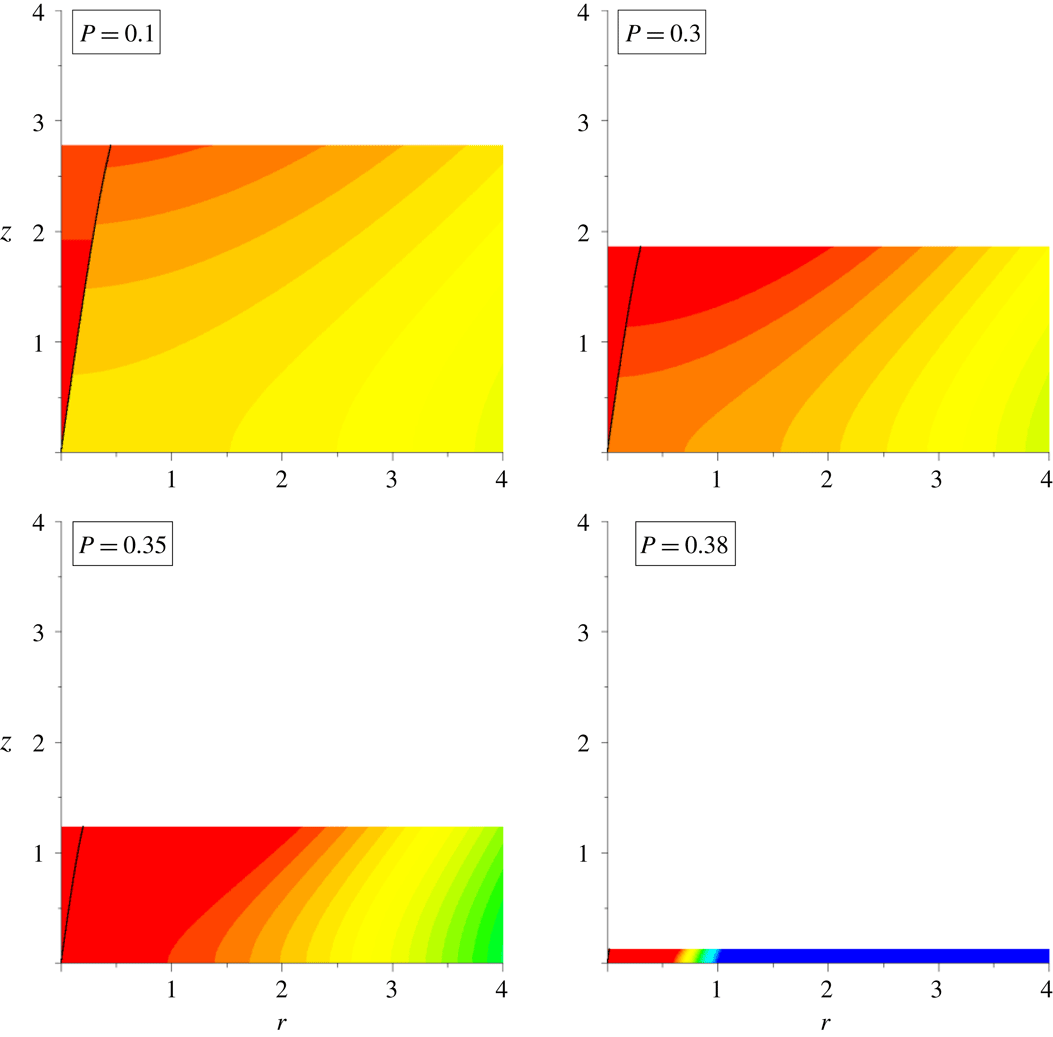
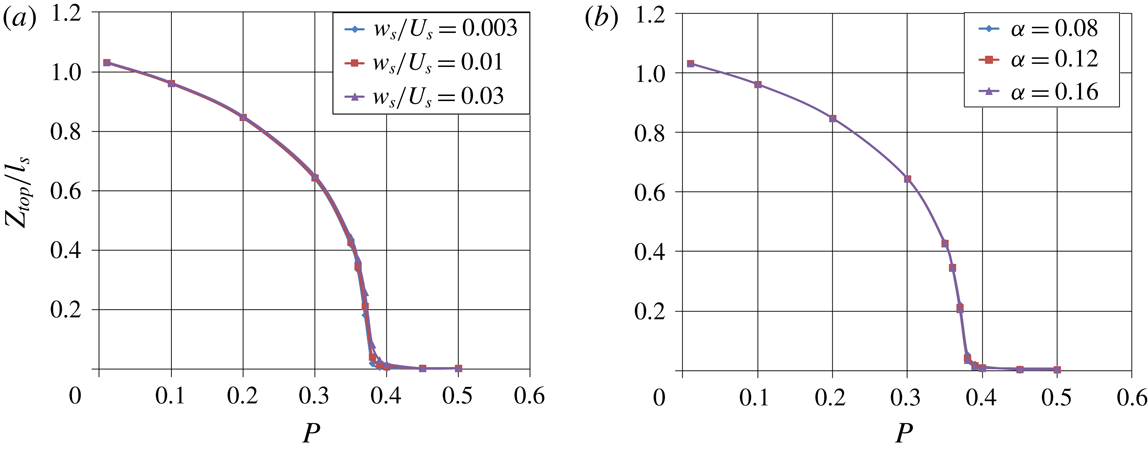
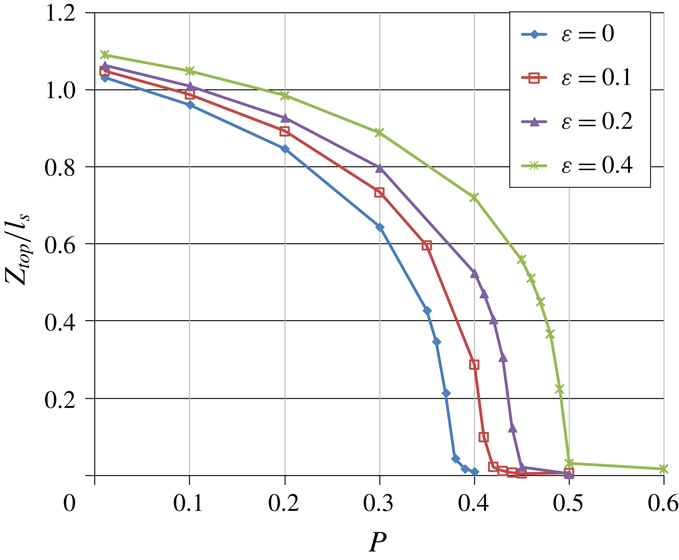
, whence the plume’s intrusion-height buoyancy
$\unicode[STIX]{x1D700}\approx 0$
, whence the plume’s intrusion-height buoyancy
![]() $B_{T}=0$
. The critical source buoyancy ratio is
$B_{T}=0$
. The critical source buoyancy ratio is
![]() $P_{crit}=0.368$
. For an investigation of the effect of overshoot-region entrainment,
$P_{crit}=0.368$
. For an investigation of the effect of overshoot-region entrainment,
![]() $\unicode[STIX]{x1D700}>0$
, see § 3.5.
$\unicode[STIX]{x1D700}>0$
, see § 3.5.
Figure 7 shows the final concentration distribution for a series of source buoyancy ratios
![]() $P$
over which the plume behaviour changes from almost unperturbed by particulate to completely ‘collapsed’. In these simulations the settling velocity is
$P$
over which the plume behaviour changes from almost unperturbed by particulate to completely ‘collapsed’. In these simulations the settling velocity is
![]() $0.01U_{s}$
and the entrainment coefficient
$0.01U_{s}$
and the entrainment coefficient
![]() $\unicode[STIX]{x1D6FC}=0.12$
. Here,
$\unicode[STIX]{x1D6FC}=0.12$
. Here,
![]() $U_{s}$
is a velocity scale based on the exact solution for a plume in an unstratified environment but at height
$U_{s}$
is a velocity scale based on the exact solution for a plume in an unstratified environment but at height
![]() $l_{s}=(1/\sqrt{\unicode[STIX]{x1D6FC}})L_{s}$
(vertical scales as in (2.5) and (2.7)):
$l_{s}=(1/\sqrt{\unicode[STIX]{x1D6FC}})L_{s}$
(vertical scales as in (2.5) and (2.7)):
To avoid distorted horizontal and vertical scaling, when scaled on source buoyancy
![]() $B_{0}$
and ambient buoyancy frequency
$B_{0}$
and ambient buoyancy frequency
![]() $N$
, horizontal and vertical lengths in the plots of figure 7 are effectively non-dimensionalised by
$N$
, horizontal and vertical lengths in the plots of figure 7 are effectively non-dimensionalised by
![]() $L_{s}$
(not
$L_{s}$
(not
![]() $l_{s}$
). Later figures will use the
$l_{s}$
). Later figures will use the
![]() $\unicode[STIX]{x1D6FC}$
-dependent scale
$\unicode[STIX]{x1D6FC}$
-dependent scale
![]() $l_{s}$
.
$l_{s}$
.
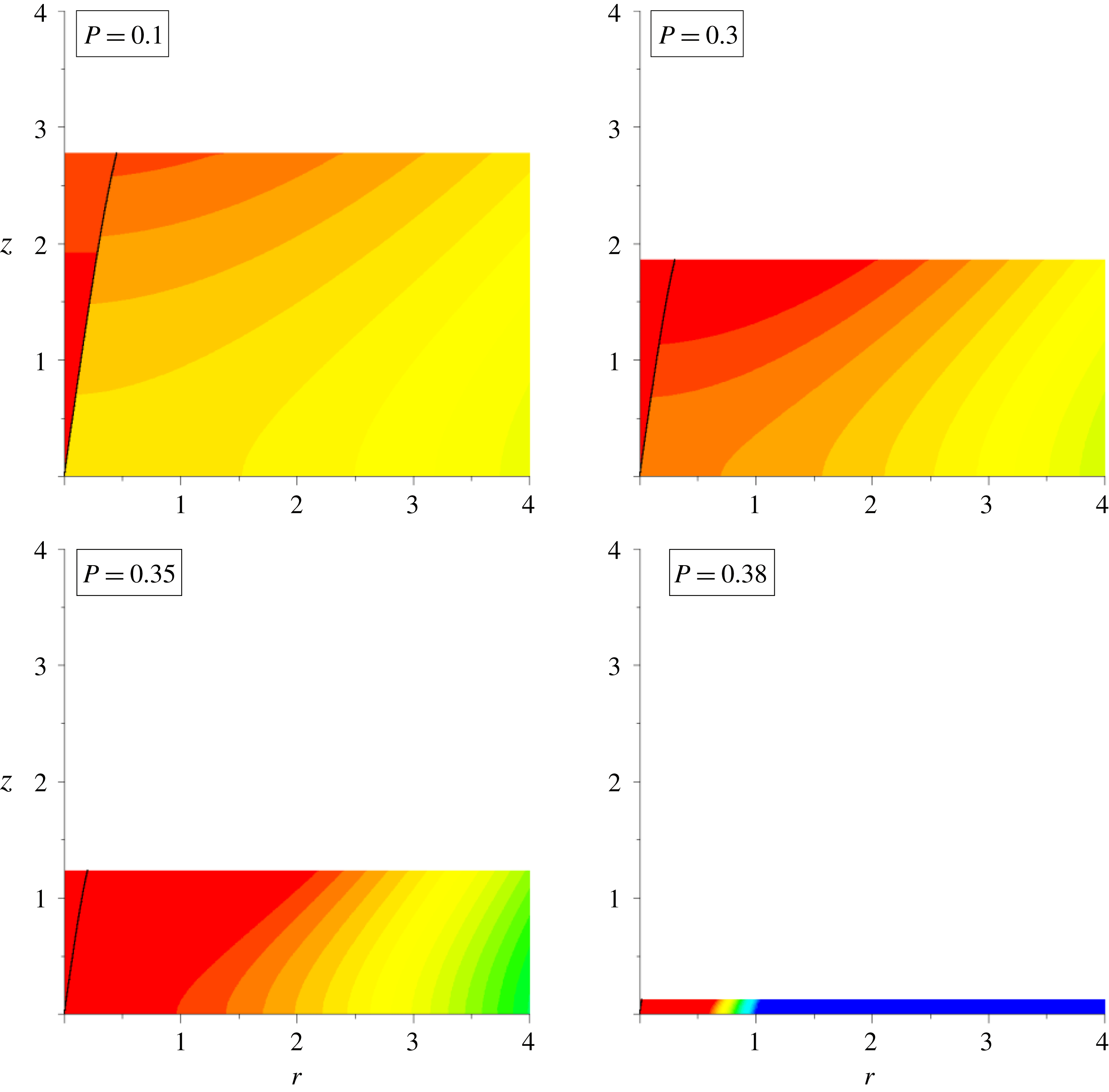
Figure 7. Final concentration distribution for various values of particle-to-fluid source buoyancy ratio
![]() $P$
; lengths non-dimensionalised by
$P$
; lengths non-dimensionalised by
![]() $L_{s}=(B_{0}/N^{3})^{1/4}$
.
$L_{s}=(B_{0}/N^{3})^{1/4}$
.
Figure 8 shows the variation of the intrusion height (relative to its initial value) in time units which are multiples of the initial fall time (
![]() $z_{0}/w_{s}$
). In all cases the height of the intrusion layer is reduced because re-entrainment of particles diminishes the overall buoyancy of the plume (see also figure 9). There is a marked change in behaviour between
$z_{0}/w_{s}$
). In all cases the height of the intrusion layer is reduced because re-entrainment of particles diminishes the overall buoyancy of the plume (see also figure 9). There is a marked change in behaviour between
![]() $P=0.36$
(non-collapsed) and
$P=0.36$
(non-collapsed) and
![]() $P=0.4$
(rapid collapse), consistent with
$P=0.4$
(rapid collapse), consistent with
![]() $P_{crit}=0.368$
. The near-critical state,
$P_{crit}=0.368$
. The near-critical state,
![]() $P=0.38$
, takes an exceptionally long time to reach its final depth.
$P=0.38$
, takes an exceptionally long time to reach its final depth.

Figure 8. Time variation (as multiple of initial fall time) of horizontal-layer height (as multiple of initial height) for various values of particle-to-fluid source buoyancy ratio
![]() $P$
.
$P$
.
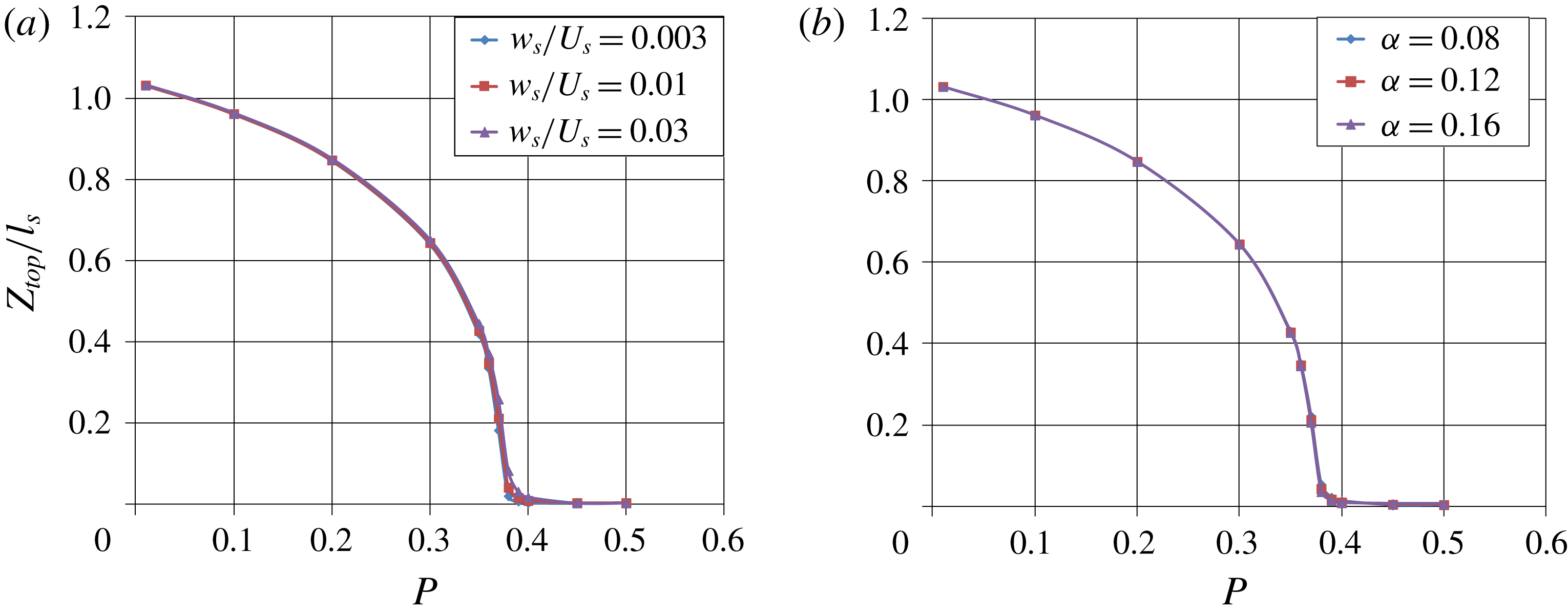
Figure 9. Final height of the intrusion layer as a function of source buoyancy ratio
![]() $P$
: (a) variation with settling velocity
$P$
: (a) variation with settling velocity
![]() $w_{s}$
; (b) variation with entrainment coefficient
$w_{s}$
; (b) variation with entrainment coefficient
![]() $\unicode[STIX]{x1D6FC}$
.
$\unicode[STIX]{x1D6FC}$
.
There are opportunities here to compare with the very simplified analysis of §§ 2.4 and 2.6 for marginal collapse, time to collapse and final intrusion height. With the intrusion height set at the neutral-buoyancy level, our predicted critical
![]() $P$
of about 0.37 is indeed observed here. Qualitatively, we note the very substantial increase in collapse time for marginal cases, as predicted in § 2.6. The time scale for collapse in the case
$P$
of about 0.37 is indeed observed here. Qualitatively, we note the very substantial increase in collapse time for marginal cases, as predicted in § 2.6. The time scale for collapse in the case
![]() $P=0.4$
is slightly larger than that predicted by (2.49), indicating that the discrete-recycling-times model, whilst indicating qualitative behaviour, underestimates the time for the intrusion height to diminish. In terms of the effect of particle loading on intrusion height for non-collapsed plumes, the simple buoyancy-based model of § 2.6 slightly underpredicts the reduction in height. For source buoyancy ratios
$P=0.4$
is slightly larger than that predicted by (2.49), indicating that the discrete-recycling-times model, whilst indicating qualitative behaviour, underestimates the time for the intrusion height to diminish. In terms of the effect of particle loading on intrusion height for non-collapsed plumes, the simple buoyancy-based model of § 2.6 slightly underpredicts the reduction in height. For source buoyancy ratios
![]() $P=0.1$
, 0.3 and 0.36, equation (2.50) predicts final-height factors 0.95, 0.72 and 0.43 respectively, which are slightly larger than the ratios 0.93, 0.62 and 0.34 observed in figure 8.
$P=0.1$
, 0.3 and 0.36, equation (2.50) predicts final-height factors 0.95, 0.72 and 0.43 respectively, which are slightly larger than the ratios 0.93, 0.62 and 0.34 observed in figure 8.
For the particle loads considered, there was no evidence of oscillatory plume collapse/recovery cycles such as those observed (in an unstratified medium) by Veitch & Woods (Reference Veitch and Woods2000).
Figure 9 shows the final height of the intrusion layer as a function of
![]() $P$
for different settling velocities and entrainment coefficient
$P$
for different settling velocities and entrainment coefficient
![]() $\unicode[STIX]{x1D6FC}$
. When intrusion height is normalised by the
$\unicode[STIX]{x1D6FC}$
. When intrusion height is normalised by the
![]() $\unicode[STIX]{x1D6FC}$
-dependent height scale
$\unicode[STIX]{x1D6FC}$
-dependent height scale
![]() $l_{s}$
all curves collapse, confirming the efficacy of this scaling. Although the time scales are not indicated by these final heights, even small particle load is observed to depress the intrusion height. However, the most significant change occurs within about 5 % of the critical value
$l_{s}$
all curves collapse, confirming the efficacy of this scaling. Although the time scales are not indicated by these final heights, even small particle load is observed to depress the intrusion height. However, the most significant change occurs within about 5 % of the critical value
![]() $P_{crit}=0.368$
.
$P_{crit}=0.368$
.
3.5 Effect of entrainment in the overshoot region
For stratification-limited plumes, the final intrusion height is affected by the amount of entrainment of particle-free fluid in the initial overshoot region, since this determines the density of fluid which forms the intrusion. In § 2.3 we formulated a relationship between the intrusion height,
![]() $Z_{T}$
, (and hence buoyancy
$Z_{T}$
, (and hence buoyancy
![]() $B_{T}$
) and the ratio,
$B_{T}$
) and the ratio,
![]() $\unicode[STIX]{x1D700}$
, of volume entrained in the overshoot region to that in the sub-intrusion rise. We noted that (a) for pure plumes, experimental evidence is that
$\unicode[STIX]{x1D700}$
, of volume entrained in the overshoot region to that in the sub-intrusion rise. We noted that (a) for pure plumes, experimental evidence is that
![]() $\unicode[STIX]{x1D700}$
is near zero, but that (b) critical source buoyancy
$\unicode[STIX]{x1D700}$
is near zero, but that (b) critical source buoyancy
![]() $P_{crit}$
would vary fairly rapidly with
$P_{crit}$
would vary fairly rapidly with
![]() $\unicode[STIX]{x1D700}$
, because the entrainment in the overshoot region is, by contrast with that below it, particle free. Thus, for any future investigation of buoyant jets, where, due to momentum, the entrainment in the overshoot region is likely to be more substantial, it is important to examine the potential effect of
$\unicode[STIX]{x1D700}$
, because the entrainment in the overshoot region is, by contrast with that below it, particle free. Thus, for any future investigation of buoyant jets, where, due to momentum, the entrainment in the overshoot region is likely to be more substantial, it is important to examine the potential effect of
![]() $\unicode[STIX]{x1D700}$
on collapse behaviour.
$\unicode[STIX]{x1D700}$
on collapse behaviour.
Using constant values
![]() $W_{s}/U_{s}=0.01$
and
$W_{s}/U_{s}=0.01$
and
![]() $\unicode[STIX]{x1D6FC}=0.12$
, figure 10 shows the variation of final height with source buoyancy ratio
$\unicode[STIX]{x1D6FC}=0.12$
, figure 10 shows the variation of final height with source buoyancy ratio
![]() $P$
for various overshoot-entrainment ratios
$P$
for various overshoot-entrainment ratios
![]() $\unicode[STIX]{x1D700}$
. Note that the time-varying maximum height
$\unicode[STIX]{x1D700}$
. Note that the time-varying maximum height
![]() $Z_{max}$
is required to compute the intrusion height (2.21), and this is still determined as the zero-momentum level in the integral plume model. In each case, the plume collapses abruptly as a critical value of
$Z_{max}$
is required to compute the intrusion height (2.21), and this is still determined as the zero-momentum level in the integral plume model. In each case, the plume collapses abruptly as a critical value of
![]() $P$
is approached. These critical values are consistent with those deduced earlier, in figure 3(c). The graph confirms that entrainment in the overshoot region makes only a small relative difference to final intrusion height, but a more substantial increase to
$P$
is approached. These critical values are consistent with those deduced earlier, in figure 3(c). The graph confirms that entrainment in the overshoot region makes only a small relative difference to final intrusion height, but a more substantial increase to
![]() $P_{crit}$
.
$P_{crit}$
.

Figure 10. Variation of intrusion-layer height with source buoyancy ratio for different degrees of entrainment in the overshoot region.
4 Conclusions
The paper starts by recapitulating a simple top-hat model for particle-free plume rise in a stratified environment. Judicious scaling based on source buoyancy,
![]() $B_{0}$
, ambient buoyancy frequency,
$B_{0}$
, ambient buoyancy frequency,
![]() $N$
, and entrainment constant,
$N$
, and entrainment constant,
![]() $\unicode[STIX]{x1D6FC}$
, reduces this to a universal set of equations and (for a pure plume) boundary conditions. In linear stratification, an additional invariant (
$\unicode[STIX]{x1D6FC}$
, reduces this to a universal set of equations and (for a pure plume) boundary conditions. In linear stratification, an additional invariant (
![]() $B^{2}+N^{2}M^{2}$
, where
$B^{2}+N^{2}M^{2}$
, where
![]() $M$
is specific momentum flux) reduces the problem further.
$M$
is specific momentum flux) reduces the problem further.
Particle loading is then considered. Using an expression for the fraction re-entrained into the plume during settling, conditions for plume collapse are deduced, based on the particle-to-fluid source buoyancy ratio,
![]() $P$
, and the plume buoyancy at the height of the intrusion layer. The latter is dependent on entrainment of ambient fluid in the overshoot region and an expression relating final height to entrainment above intrusion height is deduced. For pure plumes, comparison with experiment suggests that this additional entrainment is small and the critical source buoyancy ratio for small particles is
$P$
, and the plume buoyancy at the height of the intrusion layer. The latter is dependent on entrainment of ambient fluid in the overshoot region and an expression relating final height to entrainment above intrusion height is deduced. For pure plumes, comparison with experiment suggests that this additional entrainment is small and the critical source buoyancy ratio for small particles is
![]() $P_{crit}=0.368$
. Where there is significant source momentum, the ratio of the volume entrained in the overshoot region to that below intrusion height,
$P_{crit}=0.368$
. Where there is significant source momentum, the ratio of the volume entrained in the overshoot region to that below intrusion height,
![]() $\unicode[STIX]{x1D700}$
, is expected to be larger. A model is developed which shows that this leads to only a modest increase in intrusion height,
$\unicode[STIX]{x1D700}$
, is expected to be larger. A model is developed which shows that this leads to only a modest increase in intrusion height,
![]() $Z_{T}$
, but a much more significant increase in the critical source buoyancy ratio
$Z_{T}$
, but a much more significant increase in the critical source buoyancy ratio
![]() $P_{crit}$
. A simple estimate of time to collapse is also made, based on the number of re-entrainment cycles required to depress net plume buoyancy below that which can sustain a plume.
$P_{crit}$
. A simple estimate of time to collapse is also made, based on the number of re-entrainment cycles required to depress net plume buoyancy below that which can sustain a plume.
A more complex numerical model is then introduced, consisting of two parts: a quasi-static integral plume model for the rising plume (topped by a horizontal intrusion layer) and a time-dependent advection equation for particle concentration in ambient fluid, with the horizontal flow field determined from the entrainment velocity on the plume boundary. The model allows study of the time dependence of the particle distribution and plume, as well as incorporating particle-concentration effects on the density of entrained material. Comparison with the simpler model shows very good agreement for the minimum source buoyancy ratio
![]() $P$
at which plume collapse occurs, but indicates that the time to collapse is greater than that assuming discrete recycling intervals. Modest agreement is obtained for the final intrusion height of non-collapsing plumes. Once scaled on
$P$
at which plume collapse occurs, but indicates that the time to collapse is greater than that assuming discrete recycling intervals. Modest agreement is obtained for the final intrusion height of non-collapsing plumes. Once scaled on
![]() $l_{s}=\unicode[STIX]{x1D6FC}^{-1/2}(B_{0}/N^{3})^{1/4}$
, plume height and particle-driven collapse criteria are insensitive to particle settling velocity and entrainment coefficient. Allowance for entrainment in the overshoot region confirms the effects on intrusion height and critical buoyancy ratio proposed in the simpler model.
$l_{s}=\unicode[STIX]{x1D6FC}^{-1/2}(B_{0}/N^{3})^{1/4}$
, plume height and particle-driven collapse criteria are insensitive to particle settling velocity and entrainment coefficient. Allowance for entrainment in the overshoot region confirms the effects on intrusion height and critical buoyancy ratio proposed in the simpler model.
Both models are considerable simplifications. A top-hat model is used for plume variables; although it would be relatively straightforward to incorporate a more general profile (e.g. Gaussian) for the fluid component, this is unlikely to reflect the distribution of heavy particles which, due to re-entrainment, are more concentrated on the margins. The model depends on the entrainment assumption (and, in the case of particulate, its ability to predict the horizontal velocity field outside the plume). There is no background current; the ambient fluid is essentially stationary. Particles have a uniform size and settling velocity (although, again, it would be straightforward to amend the numerical model to deal with several different particle concentrations, each with different particle density and settling velocity). There is still imprecision in assigning the height of the intrusion layer, as experimental data are not yet sufficient to guide this in the case of particle-laden plumes. In reducing the requirements for setting it to the ratio
![]() $\unicode[STIX]{x1D700}$
of fluxes entrained above the intrusion height to that in the plume, we specify a physically interpretable parameter which we believe potentially measurable and parameterisable.
$\unicode[STIX]{x1D700}$
of fluxes entrained above the intrusion height to that in the plume, we specify a physically interpretable parameter which we believe potentially measurable and parameterisable.
Despite the simplifications, we believe that the modelling presented here provides a useful guide to the transient behaviour of particle-laden plumes in a stratified environment. The focus has been on pure plumes in linearly stratified environments (although the detailed computational model actually has neither of these restrictions) and thus is suitable for further investigations on forced plumes (with significant source momentum, and likely higher entrainment in the overshoot region) and more complex stratification.
Acknowledgements
The authors are indebted to the associate editor and the anonymous reviewers, particularly one whose emphasis on the overshoot region led us to derive a more physically justifiable expression for intrusion height.